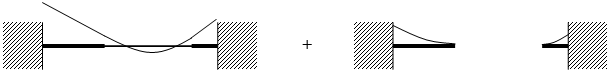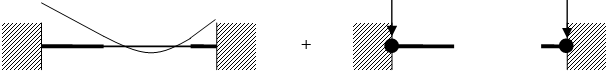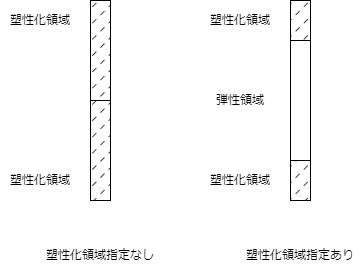計算編のサブセクション
01. 荷重計算
01. 荷重計算のサブセクション
柱梁自重
柱梁自重の計算
RC梁・SRC梁
(1) 単位長さ当りの重量
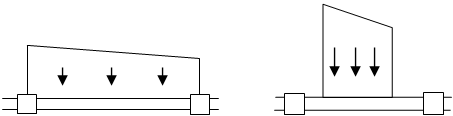
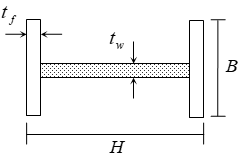
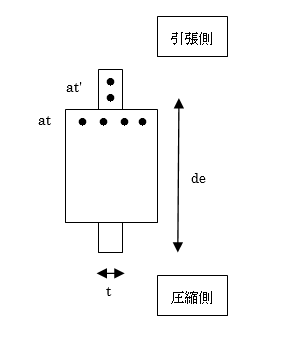
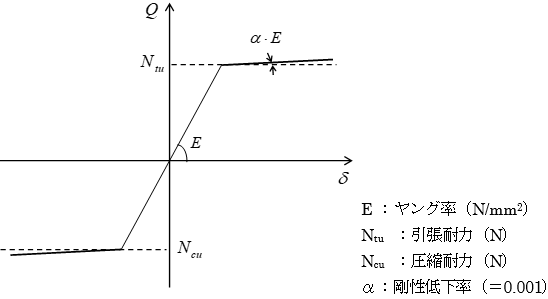
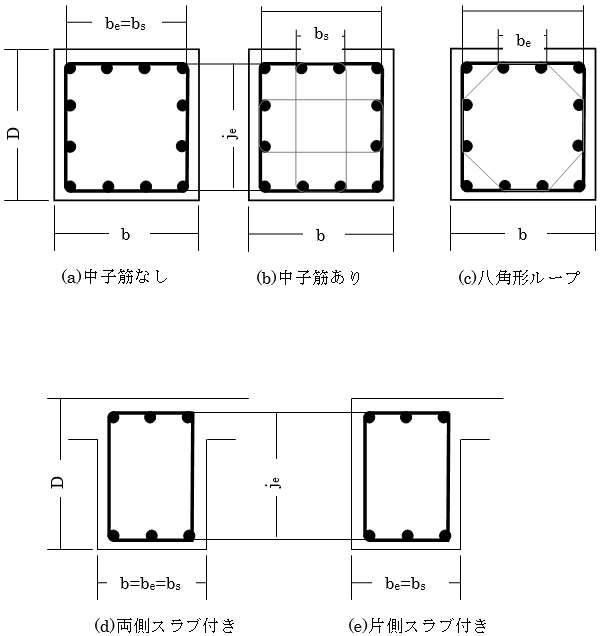
鉄筋コンクリート(RC)・鉄骨鉄筋コンクリート(SRC)造の大梁、小梁、片持ち梁の単位長さ当りの重量は、スラブの取付きにかかわらず下式により算定します。式中のコンクリートの単位体積重量( $γ$)は鉄筋、鉄骨重量を含みます。位置ごとに断面が異なる場合は中央断面を採用します。
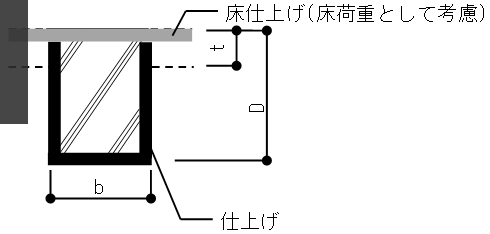
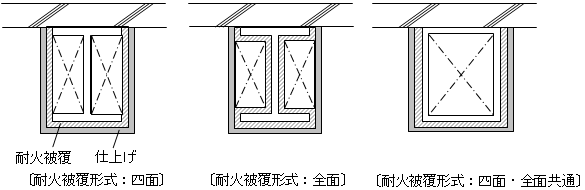
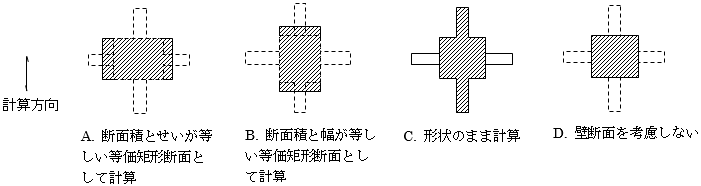
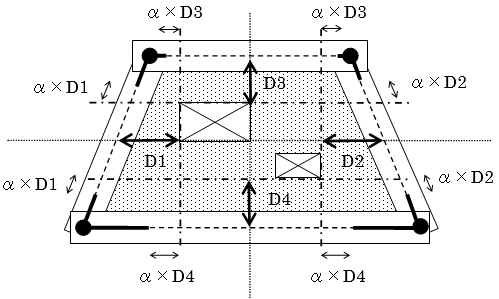
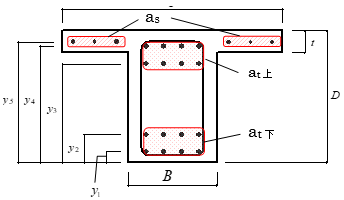
仕上げ荷重は、部材・階ごとに指定できます注1)。 仕上げ形式は、 下図に示す四面仕上げとします。
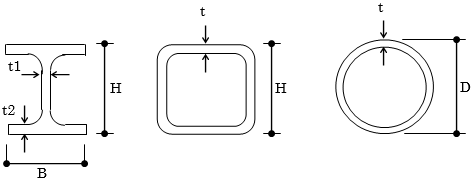
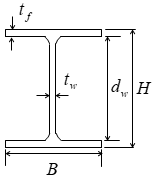
$$ w_c = γ \cdot b(D-t)+w_f(b+2D) $$$γ$:コンクリートの単位体積重量(鉄筋・鉄骨重量を含む)(kN/m3)
$b$:梁幅(m)
$w_f$:仕上げ重量(kN/m2)
$D$:梁せい(m)
$t$:スラブ厚
上図の $t$はスラブ厚を指します。
| 種類 | 設計基準強度の範囲(N/mm2) | γC(kN/m3) | γRC(kN/m3) | γSRC(kN/m3) |
|---|---|---|---|---|
| 普通コンクリート | Fc≦36 | 23.0 | 24.0 | 25.0 |
| 36<Fc≦48 | 23.5 | 24.5 | 25.5 | |
| 48<Fc≦60 | 24.0 | 25.0 | 26.0 | |
| 60<Fc≦80 | 24.0 | 25.0 | 26.0 | |
| 80<Fc≦100 | 24.0 | 25.0 | 26.0 | |
| 100<Fc≦120 | 24.0 | 25.0 | 26.0 | |
| 120<Fc≦150 | 24.5 | 25.5 | 26.5 | |
| 軽量コンクリート1種 | Fc≦ 27 | 19.0 | 20.0 | 21.0 |
| 27<Fc≦ 36 | 20.0 | 22.0 | 23.0 | |
| 軽量コンクリート2種 | Fc≦ 27 | 17.0 | 18.0 | 19.0 |
$γ_{C}$:コンクリートの気乾単位体積重量
$γ_{RC}$:鉄筋コンクリートの単位体積重量
$γ_{SRC}$:鉄骨鉄筋コンクリートの単位体積重量
注1) メインメニュー「荷重・材料」→「柱・大梁仕上げ」→「RC造(仕上重量)」参照。
異種強度においても同種強度梁と同様の方法(使用材料で指定する「床スラブ・梁のFc」を用いて比重を計算する)で計算します。
梁重量の算定に用いる梁の長さは以下のように計算します。
(2) 梁の長さ
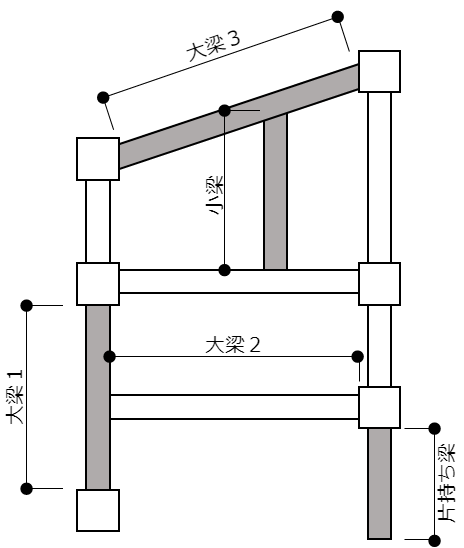
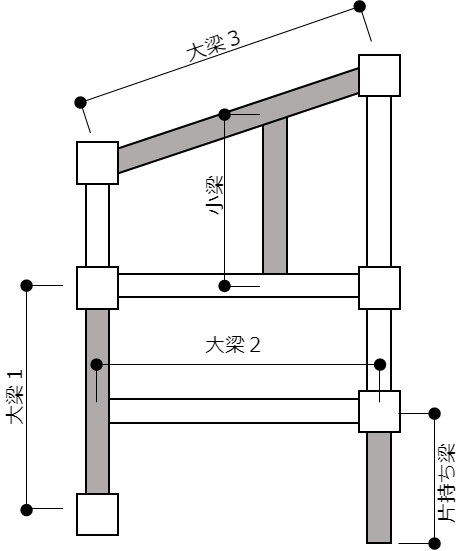
大梁
・両端が柱の場合は柱面間距離とします。(大梁-1)
・片側が大梁の場合は梁面から柱面までの距離とします。(大梁-2)
・梁が斜めの場合は節点距離-両側の柱幅の合計/2とします。(大梁-3)
小梁
・両端の大梁面間距離とします。ただし、大梁と小梁が直交していない場合でも大梁と小梁の重複部分の長さは大梁幅の半分として計算します。
・小梁位置で大梁が分割されていて節点と小梁が接続している場合は、節点に接続する大梁の平均幅から重複部分を計算します。
片持ち梁
・柱面から片持ち梁先端までの距離とします。
RC・SRC柱
(1) 単位長さ当りの重量
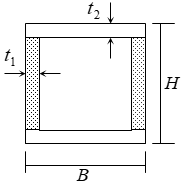
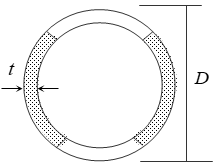
RC・SRC造の柱の単位長さ当りの重量は、下式によります。式中のコンクリートの単位体積重量( $γ$)には鉄筋、鉄骨重量を含みます。
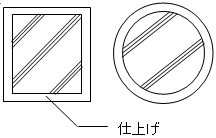
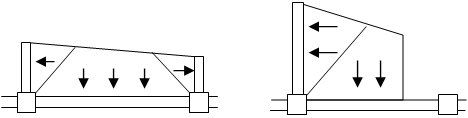
仕上げ荷重は部材・階ごとに指定できます(“RC梁・SRC梁”)。仕上げ形式は、下図に示す四面仕上げとします。柱頭・柱脚で断面が異なる場合は、柱脚の断面を採用します。
$w_c = \gamma \cdot A_c+w_f \cdot \phi$$γ$:コンクリートの単位体積重量(鉄筋・鉄骨重量を含む)(kN/m3)
$A_c$:柱断面積(m2)
$w_f$:仕上げ重量(kN/m2)
$φ$:仕上げ周長(m)
(2) 柱の長さ
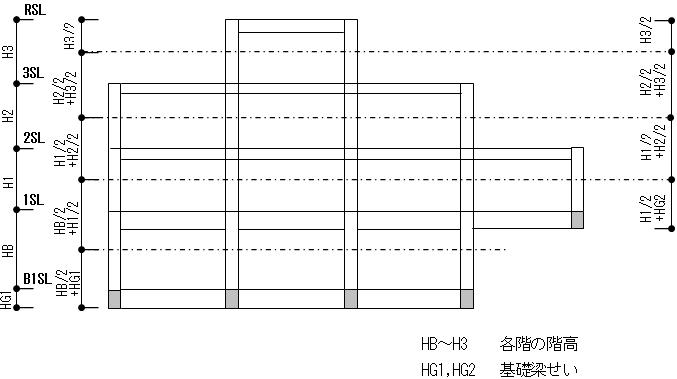
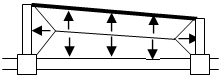
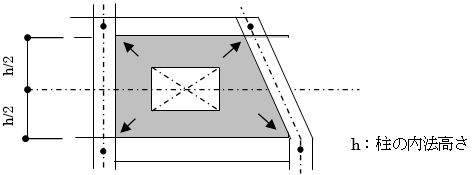
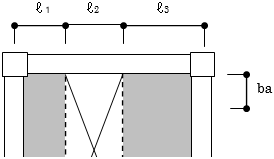
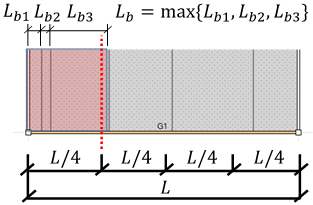
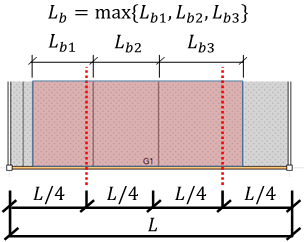
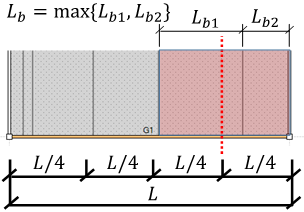
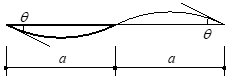
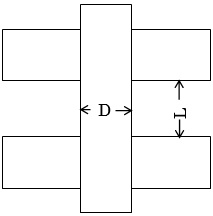
柱重量算定に用いる柱長さは床上面から床上面までとし、柱重量は階の中央で上下階に振り分けます。RC・SRC造の柱において、下階に柱がない場合は、柱脚に取付く梁の最大せいの長さ(下図のハッチ部分)を柱長さに付加します。
鉄骨梁
(1) 単位長さ当りの重量
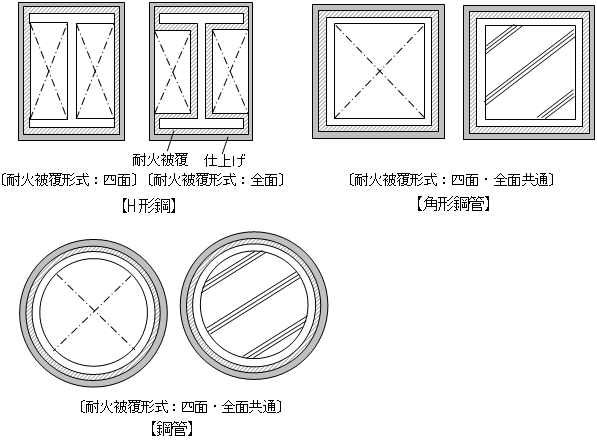
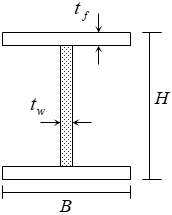
S造の梁の単位長さ当りの重量は、下式により算定します。仕上げ荷重は部材・階ごとに指定、耐火被覆重量および被覆厚は階ごとに指定できます注1)。仕上げ形式は下図に示す四面形式とし、耐火被覆形式は部材ごとに指定が可能です注1)。位置ごとに断面が異なる場合は中央断面を採用します。
$ w_s = \alpha \cdot \gamma_s \cdot A_s+\gamma_f \cdot \phi+\gamma_c \cdot A_c$$α$:鉄骨重量割増率
$γ_s$:鉄骨の単位体積重量( $γ_s$=77kN/m3)
$A_s$:鉄骨の断面積(m2)
$φ$:仕上げ周長(m)
$γ_f$:仕上げ重量(kN/m2)
$γ_c$:耐火被覆重量(kN/m3)
$A_c$:被覆材の断面積(m2)
(2) 梁の長さ
梁重量の算定に用いる梁の長さは以下のように計算します。
大梁
・節点間距離とします。(大梁1,2,3)
小梁
・節点間距離とします。
片持ち梁
・柱節点から片持ち梁先端までの距離とします。
注1) メインメニュー「荷重・材料」→「柱・大梁仕上げ」参照。
鉄骨柱
(1) 単位長さ当りの重量
S造の柱の単位長さ当りの重量は、下式により算定します。仕上げ重量、仕上げ形式、および耐火被覆形式の指定については、鉄骨梁と同様です。柱頭・柱脚で断面が異なる場合は、柱脚の断面を採用します。
$ w_s = \alpha \cdot \gamma_s \cdot A_s+\gamma_f \cdot \phi+\gamma_c \cdot A_c$$α$:鉄骨重量割増率
$γ_s$:鉄骨の単位体積重量( $γ_s$=77kN/m3)
$A_s$:鉄骨の断面積(m2)
$φ$:仕上げ周長(m)
$γ_f$:仕上げ重量(kN/m2)
$γ_c$:耐火被覆重量(kN/m2)
$A_c$:被覆材の断面積(m2)
(2) 柱の長さ
柱重量の算定に用いる柱長さは、RC柱と同様です。(“RC・SRC柱 柱の長さ”)
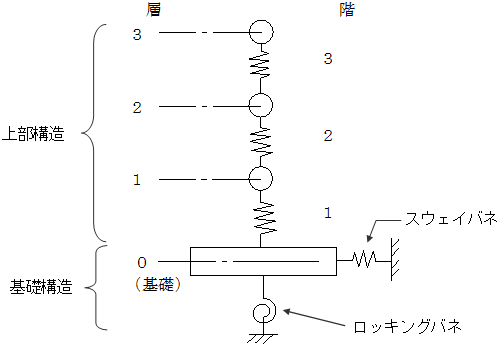
間柱型ダンパー
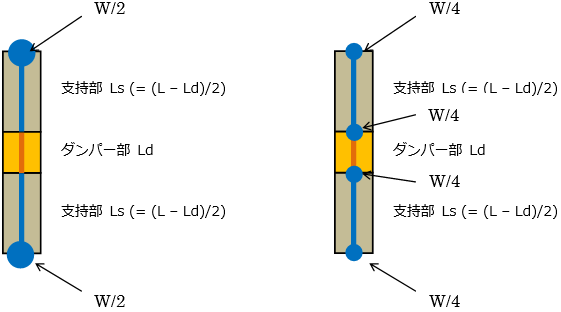
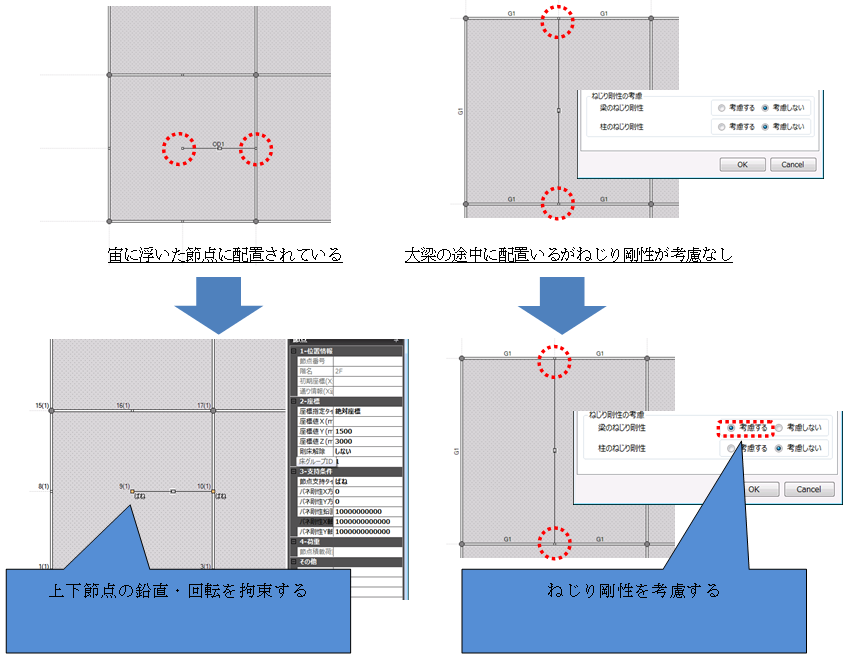
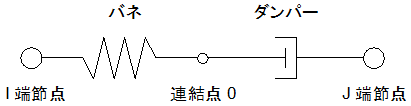
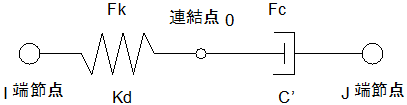
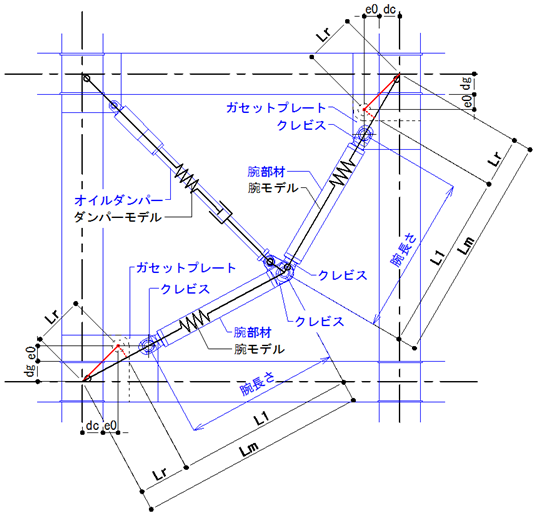
間柱型ダンパーの重量は上下節点に分配されます。ただし、画像右のダンパー(JFEシビル間柱型粘弾性ダンパー)は解析モデル上の中間節点にも重量が分配されます。
スラブ、片持ちスラブの荷重伝達
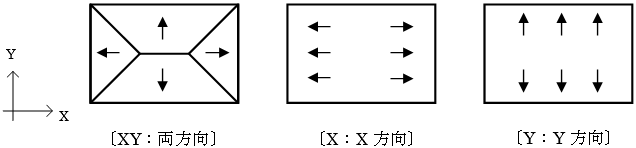
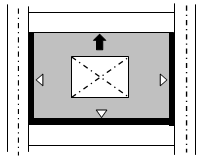
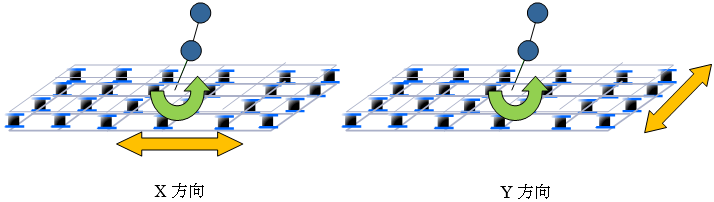
床荷重の伝達方向は、両方向、X方向、Y方向とします。荷重の伝達方向の指定は、床を配置する際に床ごとに行います。
〔XY〕 :両方向に伝達する。
〔X〕 :X方向に伝達する。
〔Y〕 :Y方向に伝達する。
- 床の重量は構造芯間の面積について計算します。小梁で構成された床組の重量は、小梁芯により区分された床面積について求めます。
- 大梁のCM0Q0は、床の荷重伝達方向と小梁による分割を考慮して算定します。
- 小梁負担分の荷重については、小梁のQ0がその小梁を支持する小梁または大梁に作用するものとして計算します。小梁自重も同様に扱います。
スラブ
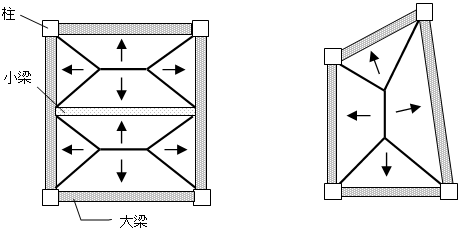
(1) 両方向伝達の床割り
四辺を梁で囲まれたスラブについては、荷重の伝達方向が両方向の場合、床スラブから梁に加わる鉛直荷重は、1999年版RC規準10条により下図のようになります。具体的には、スラブに取付く梁は、梁の交点から描いた2等分線および梁に平行な直線から作られる台形、または三角形の部分の荷重を受けるものと見なします。
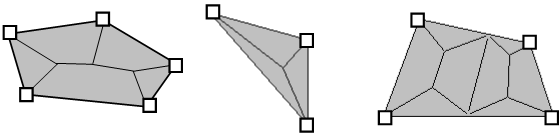
(2) 多角形の床組の適応
本プログラムは、以下に示す多角形の床組に適用しています。
〔五角形〕 〔三角形〕 〔台形〕
片持ちスラブ
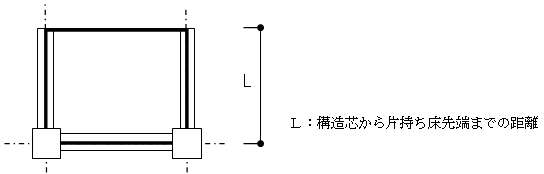
(1) 片持ちスラブ
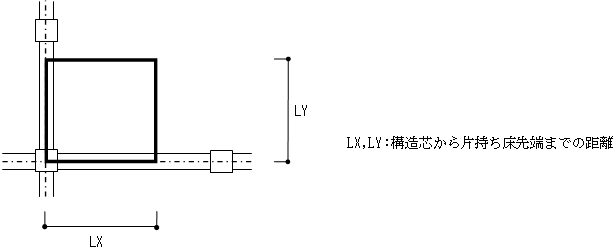
片持ちスラブの重量は、構造芯から片持ち床先端までの面積について計算します。
片持ちスラブの荷重は、片持ち梁の取り付きおよび先端リブ小梁の取り付きによって以下のように伝達されます。
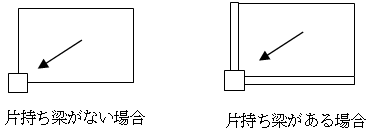
・片持ち梁がない場合 : 全て大梁に伝達されます。
・片持ち梁がある場合 : 片持ちスラブが接続する大梁、片持ち梁に対してスラブと同様のルールにより分割して荷重伝達されます。
・片持ち梁と先端リブ小梁がある場合 : 片持ちスラブが接続する大梁、片持ち梁先端リブ小梁に対して スラブと同様のルールにより分割して荷重伝達されます。
先端リブ小梁がある場合はスラブ幅は片持ち梁の先端までと見なされます。
(2) 出隅の片持ちスラブ
スラブ荷重及び先端の線荷重の梁、柱への荷重伝達は以下のようになります。出隅の重量は、構造芯から出隅先端までの長方形について計算します。
出隅の片持ちスラブの荷重は、荷重伝達方向および片持ち梁の取付きに関わらず、節点荷重としてすべて柱に伝達します。
(3) 入隅の片持ちスラブ
本プログラムは、現状では入隅の片持ちスラブには対応しておりません。
壁自重
壁の固定荷重
共通事項
(1) 柱軸力算定時
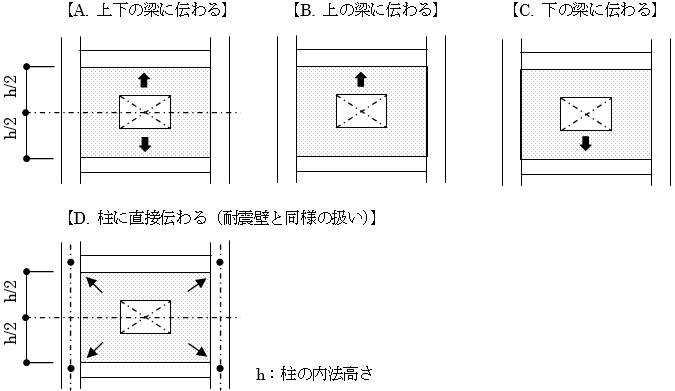
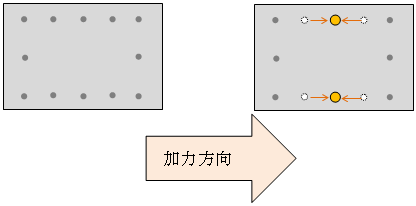
鉛直荷重における柱軸力を算定する場合、地震用重量における節点重量を算定する場合には、壁の重量を階高の中央で上下階の節点に分配するものとします。
(2) 大梁 $CMoQo$算定時
壁の重量は階高の中央で上下階の節点に分配し、梁の $CMoQo$には考慮しません。
壁に三方スリットが指定されている場合、壁荷重は全て上部の大梁に伝達され、大梁の $CMoQo$に考慮されます。
壁
(1) 耐震壁
耐震壁の重量は周辺の柱梁の内法寸法で計算します。梁にハンチがある場合や、セットバック等で柱梁が斜めの場合は、それらを考慮して算定します。荷重は、階高の中央で上下階の節点に分配するものとします
開口がある場合には形状・位置及び開口重量を考慮して計算します。
壁の仕上げ荷重は、片面仕上げとして計算します。
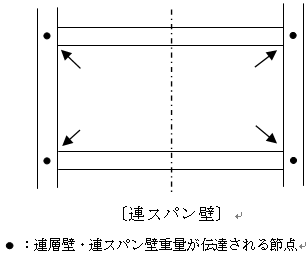
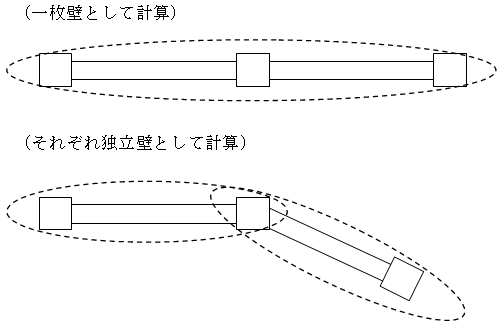
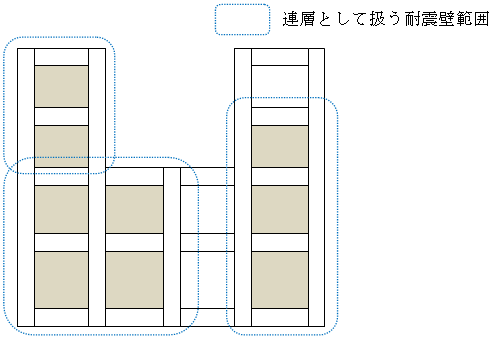
(2) 連スパン壁
壁寸法、開口の扱い、仕上げについては一般壁と同様に計算します。
壁重量は壁の上下左右の4節点に振り分けられ、連スパン壁における途中スパンの重量には考慮されません。
(3) 非耐震壁
非耐震壁の重量の計算方法は、以下の指定によります。仕上げ壁のみの場合は、非耐震壁の自重伝達方法によります。
ダンパー自重
ダンパーの自重
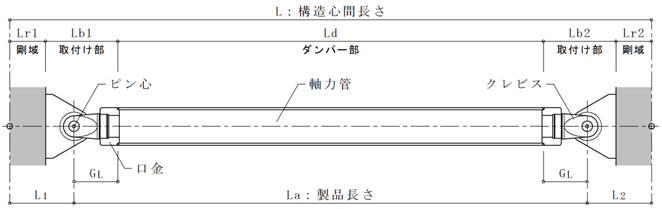
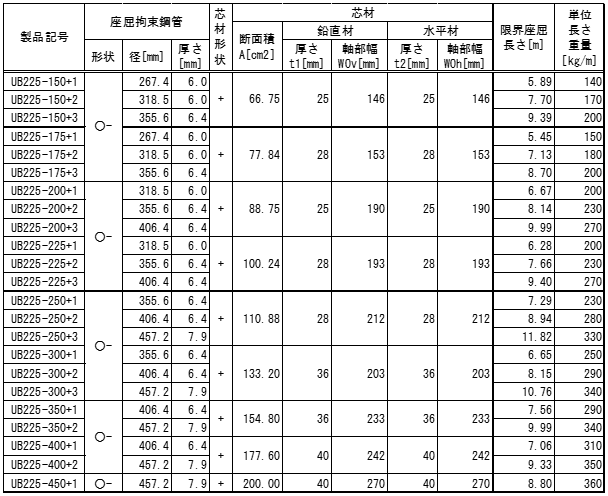
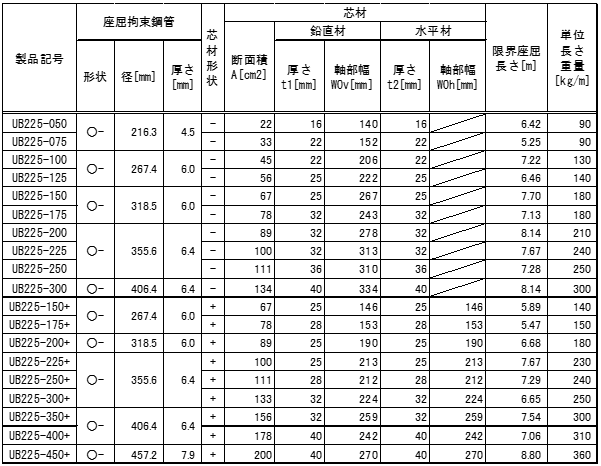
座屈拘束ブレース(直接入力)
単位長さ当りの装置重量の入力に対して、節点間距離を乗じて自重とします。
オイルダンパー
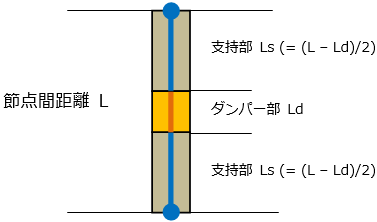
ダンパー部の装置重量(入力値)と、支持部断面積×(節点間距離 - 装置長さ)×鋼材単位体積重量の合計値を自重として計算します。
自重を考慮しない部材
ダンパー部分の自重を考慮しない部材
以下の部材はダンパー部分の自重を考慮しません。 (間柱ダンパーについては支持部の重量は考慮されます。)
- 日鉄住金関西工業 SUB
- 免制震ディバイス RDTダンパー
- 免制震ディバイス iRDTダンパー
- オイレス工業 粘性制振壁
- 免制震ディバイス 粘性制振壁
- 日鉄エンジニアリング ユニットゴムダンパー
- 住友理工TRCダンパー
- JFEシビル 間柱型粘弾性ダンパー
- 各社 免震支承材
- 各社 免震減衰材
CMoQの計算
CMoQの計算
柱のCMoQ
土圧・水圧等による柱のCMoQについては考慮されません。
大梁のCMoQ
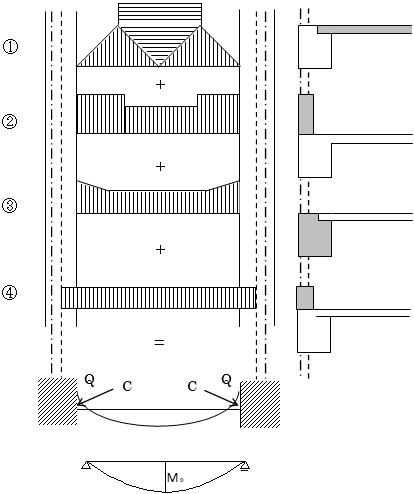
大梁のCMoQには以下の①から④を考慮します。なお、ダミー梁を介して伝達される荷重はダミー梁が接続する節点に節点荷重として伝達します。
①小梁、片持ち床などを含む床荷重によるCMoQo
②壁荷重によるCMoQ
③梁自重によるCMoQ
④パラペットや手すり等、特殊荷重によるCMoQ
剛域の考慮
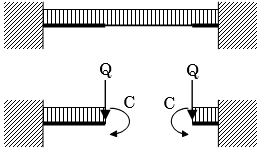
「荷重条件」の設定により、剛域部分を考慮して大梁のCMoQを計算することができます。剛域を考慮する場合には、まず可撓部分で固定端モーメントとせん断力を計算します。次に、可撓部分で計算された端部応力を外力として片持ち梁として仮定した剛域部分の先端に作用させます。結果として計算される剛域部片持ち梁の元端モーメントおよびせん断力を大梁全体の固定端モーメントおよびせん断力として考慮します。
また、剛域部分の荷重計算方法は下記から選択できます。
「剛域を考慮する(剛域部外力はCMoQに加算する)」
「剛域を考慮する(剛域部外力は柱に伝達する)」
地震荷重の計算
地震荷重
地震用節点重量
地震用節点重量は、下記の値を節点毎に集計して求めます。
・大梁のCMoQoの計算で求めた梁せん断力
床の積載荷重は地震用の値とします。
・直接入力による節点荷重
層せん断力
全剛床の設計用せん断力
地震用節点重量を層毎に集計し、建築基準法に基づき層せん断力を求めます。
(1) 一般階
$Q_i =C_i \sum_{j=i+1}^{n+1} W_j$$Q_i$ :i階の層せん断力
$W_j$ :j層の層重量
$n$ :階数
$C_i$ :層せん断力係数
$C_i=Z・R_t・A_i・C_o$
ただし、
$C_i$ :層せん断力係数
$Z$ :地震地域係数
$R_t$ :振動特性係数
$R_t=1$ ( $T<T_c$の場合)
$R_t= 1-0.2(T/T_c-1)^2$ ( $T_c≦T<2・T_c$の場合)
$R_t=1.6 T_c/T$ ( $2・T_c≦T$の場合)
$T$ :建築物の設計用1次固有周期
〔略算法〕
$T=h・(0.02+0.01・α)$$h$ :建築物の高さ
$α$:当該建築物のうち柱及び梁の大部分が鉄骨造である階※の高さの合計hに対する比
※「階・軸の設定」の階高設定部分における構造種別がS造になっている階
〔精算法〕
直接入力
$T_c$ :地盤種別から決まる下表の係数
| 第1種地盤 | 0.4 |
| 第2種地盤 | 0.6 |
| 第3種地盤 | 0.8 |
$A_i$ :層せん断力係数の分布係数
$C_o$ :標準せん断力係数
(2) PH階
$ Q_i =k \sum_{j=i+1}^{n+1} Wj$$k$ :震度(1.0~0.5を直接指定する。)
(3) 地下階
$Q_i=Q_{i+1}+K_i・W_i$ $K_i=0.1・(1-H_i/40)・Z$
$H_i$ :各部分の地盤面からの深さ(m)(20mを超える場合は20mとする。)
$Z$ :地震地域係数
多剛床の設計用せん断力
多剛床の場合地震層せん断力は以下の方法により計算されます。
副剛床の $C_i$を直接入力しない場合 : 階全体の総重量から層せん断力を算出し、それによって求まる水平力を剛床ごとの重量比で分配します。
副剛床の $C_i$を直接入力した場合 : 主剛床は上記の全剛床の場合の $C_i$に従って層せん断力を計算します。副剛床は指定した $C_i$を用いて層せん断力を計算します。
水平力
(1) 建物設計用水平力
水平力は各節点に作用させます。各層の等価震度を下の式で求め、それを各節点の地震用節点重量に乗じて、地震時水平力を求めます。
$K_i=(Q_i-Q_{i+1})/W_i$$K_i$ : $i$層の等価震度
$Q_i$ : $i$階の層せん断力
$W_i$ : $i$層の層重量
(2) 床面積
床面積は芯々で計算し、片持ちスラブ部分の床面積も算入します。また、床スラブを配置していない場合でも、小梁を入力している場合は吹き抜け部分の床面積を算入します。
風荷重の計算
風圧力
風用節点重量
風圧力は、建築物の側面に対してX方向、Y方向についてそれぞれ別に働くものとし、風圧力をうける側面に存在している各節点に、節点荷重として作用させ応力解析を行います。
(1) 風圧力
速度圧と風力係数から、風圧力を計算します。
$W = Cf・q・A$ここで $W$ :風圧力(N)
$Cf$ :風力係数
$Cf = C_{pe}-C_{pi}$
風圧力係数は各階ごとで直接入力することもできます。作用方向が、左→右加力では左側を風上壁面Cf、右側を風下壁面Cfとし、右→左加力では左側を風下壁面Cf、右側を風上壁面Cfを用います。
$C_{pe}$ :建築物の外圧係数
| 部位 | 風上壁面 | 風下壁面 |
|---|---|---|
| Cpe | 0.8kz | -0.4 |
※係数"0.8"および"-0.4"は指定した数値を用います。
$C_{pi}$ :建築物の内圧係数(指定による)
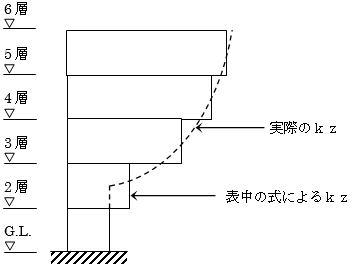
$k_z$ :以下の表により、計算した数値
| HがZb以下の場合 | 1.0 | |
|---|---|---|
| HがZbを超える場合 | ZがZb以下の場合 | $\left( \frac{Zb}{H} \right)^{2\alpha}$ |
| ZがZbを超える場合 | $\frac{\int_{Zi}^{Zi+1}(\frac{Z}{H}) ^{2\alpha}dz}{Z_{i+1}-Z_i}$ |
図中2階のように2つの式にまたがる場合も平均のKzを求めます。
$Z$ :地盤面から各層床位置までの高さ(m)
$q$ :速度圧(N/m2)
$q$ = 0.6・E・V02
$V_0$ :基準風速(m/s)(指定による。)
$E$ :建築物の屋根の高さ及び周辺の地域に存する建築物その他の工
作物、樹木その他の風速に影響を与えるものの状況に応じた係数
で、以下の方法により算出します。
$E$ = $Er^2・Gf$
$Er$ :平均風速の高さ方向の分布を表す係数
$H$が $Z_b$以下の場合: $Er$ = $1.7(Z_b/Z_G)^α$
$H$が $Z_b$を超える場合: $Er$ = $1.7(H/Z_G)^α$
$H$ :建築物の高さと軒の高さとの平均(m)
GLからPH階を除く最上階の床高さ+パラペット高さの半分
$A$ :見付け面積(m2)
$Z_b$, $Z_G$, $α$ :地表面粗度区分から求まる係数で、以下の表によります。
表) 地表面粗度区分
| 地表面粗度区分 | Zb[m] | ZG[m] | α | |
|---|---|---|---|---|
| Ⅰ | 都市計画区域外にあって、極めて平坦で障害物が無いものとして特定行政庁が規則で定める区域 | 5 | 250 | 0.10 |
| Ⅱ | 都市計画区域外にあって地表面粗度区分Ⅰの区域以外の区域(建築物の高さが13m以下の場合を除く。) 又は都市計画区域内にあって地表面粗度区分Ⅳの区域以外の区域のうち、海岸線又は湖岸線(対岸までの距離が1,500m以上のものに限る。以下同じ。)までの距離が500m以内の地域(ただし、建築物の高さが13m以下である場合又は当該海岸線若しくは湖岸線からの距離が200mを超え、かつ、建築物の高さが31m以下である場合を除く。) | 5 | 350 | 0.15 |
| Ⅲ | 地表面粗度区分Ⅰ、Ⅱ又はⅣ以外の区域 | 5 | 450 | 0.20 |
| Ⅳ | 都市計画区域内にあって、都市化が極めて著しいものとして特定行政庁が規則で定める区域 | 10 | 550 | 0.27 |
$Gf$ :ガスト影響係数
地表面粗度区分および $H$に応じて、次の表に掲げる数値とします。
表) 構造骨組用ガスト影響係数
| H | (1) | (2) | (3) |
|---|---|---|---|
| 地表面粗度区分 | 10m以下の場合 | 10mを超え、40m未満の場合 | 40m以上の場合 |
| Ⅰ | 2.0 | (1)と(3)とに掲げる数値を 直線的に補間した数値 | 1.8 |
| Ⅱ | 2.2 | 2.0 | |
| Ⅲ | 2.5 | 2.1 | |
| Ⅳ | 3.1 | 2.3 |
(2) 風圧力を受ける面と見付面積
風圧力を受ける面は、壁面(垂直面)とします。 屋根面および、地下階の壁、および外部袖壁、パラペットは考慮しません。
見付面積は、建物外周の通り芯間と梁天端間とからなる無開口壁が存在するものと仮定し、絶対座標系のX方向、Y方向それぞれについて、セットバックや軸振れなどの節点移動を無視した垂直面とします。
02. 剛性計算
02. 剛性計算のサブセクション
RC大梁
RC大梁の剛性
剛性増大率
軸断面積
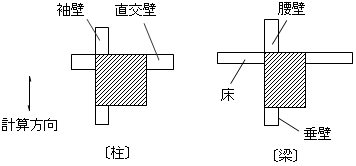
梁の断面積は腰壁・垂壁を考慮します。腰壁・垂壁のヤング係数は母材と同じと仮定します。
断面二次モーメント
梁の断面2次モーメントは、柱と同じ算定方法により計算します 注1)。
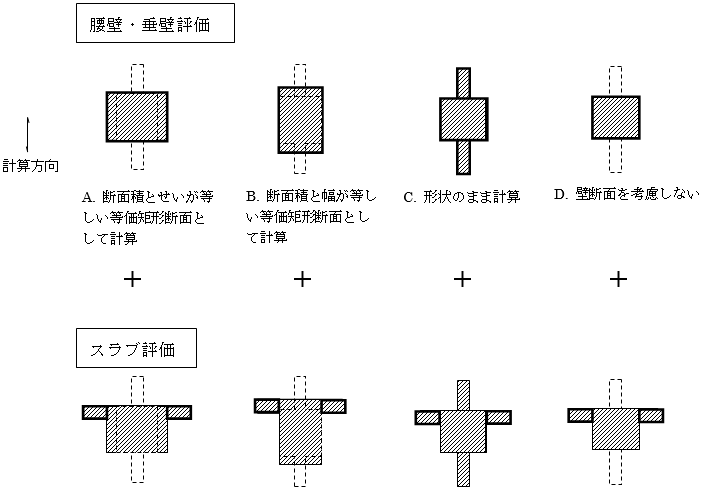
$A~C$を選択した場合は、腰壁・垂壁を評価して断面2次モーメント
$I$を求めます。上記の
$A$または
$B$の評価は腰壁・垂壁のみについて等価断面として考慮し、床は別途計算し加算します。
$C$の評価の場合、腰壁・垂壁および床をすべて形状通り評価します。中立軸はいずれの場合も床スラブを考慮した中立軸を採用します。床の厚さは、建物全体で一律に設定できます 注1)。
床については、
$A$.協力幅による自動計算、または
$B$.剛性増大率の直接入力により剛性の評価方法を設定できます 注1)。二重スラブとして配置した床は、荷重のみを評価して剛性は考慮しません。また、片持ちスラブを剛性として考慮するかどうかについては「剛性条件」により設定できます。
※「鉄筋・鉄骨の剛性を考慮する」とした場合には剛性増大率は変化せず、剛性増大率を乗じる元となる断面2次モーメントを増大させます。
注1) メインメニュー「設計・計算条件」→「剛性条件」参照。
協力幅の計算
a) 協力幅による自動計算
協力幅はRC規準8条「構造解析の基本事項」により算定します。床の厚さは建物全体で一律に設定します注1)。
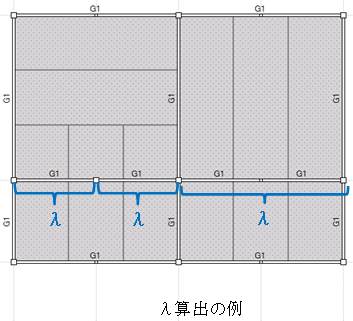
床組みを構成する大梁のうち以下のすべての条件を満たす大梁群は連続梁と見なしてλを算出します。
・方向が同じ大梁
・直線上に配置されている大梁
・中間に柱が存在しない
- λ算出の例
吹抜けがある場合は、床の長さの比を倍率としてbaにかけて算定します。
$ba' = \frac{l_1+l_3}{l_1+l_2+l_3} \cdot ba$※床荷重リストで床厚を0[mm]とした床は吹抜けと同様に扱います
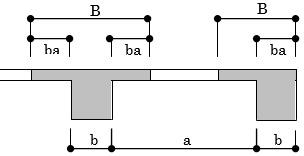
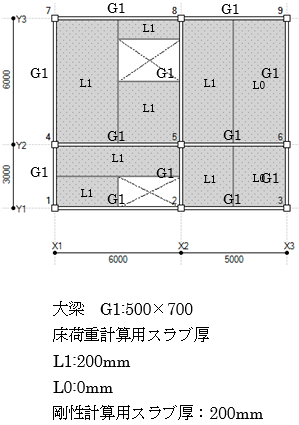
協力幅の計算例を以下に示します。
下図のような平面において、
(大梁1-2の場合)
$ba = \left( 0.5-0.6\times\frac{2.5}{6.0} \right) \times2.05\times \frac{3.0}{3.0+3.0}=0.313$
$B = 0.5+0.313 = 0.813$
(大梁2-3の場合)
$ba = 0.1\times5.0\times \frac{2.5}{2.5+2.5}=0.250$
$B = 0.5+0.250 = 0.750$
(大梁5-8の場合) $ba1 = 0.1\times6.0\times \frac{3.0+1.0}{3.0+2.0+1.0}=0.4000$
$ba2 = 0.1\times6.0=0.6000$
$B = 0.5+0.400+0.6000=1.500$
(大梁8-9の場合)
$ba = 0.1\times5.0\times \frac{2.5}{2.5+2.5}=0.250$
$B = 0.5+0.250=0.750$
b) 剛性増大率の直接入力
片側スラブ、両側スラブごとに剛性増大率を用いて算定します。
構造スラブ符号指定
床に対して構造スラブ符号を指定した場合、梁上部のコンクリートは梁に指定したコンクリート材料によるヤング係数を採用し、梁の片側もしくは両側に取り付くスラブについては設定した構造スラブのコンクリート材料によるFcを採用します。
RC大梁の断面性能
鉄筋コンクリート造梁の断面性能の計算は以下によります。
軸断面積( $A_n$)
梁の軸断面積( $A_n$)は、鉄筋を考慮して次式により算定します。
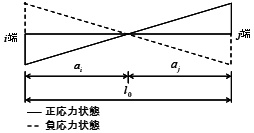
$A_n=({B \cdot (D-t)+B \cdot t+(n-1) \sum \alpha_i}) \cdot \frac{l_0}{l}$$n$:ヤング係数比
$l_0$:可撓長さ(剛域を考慮した長さ)(mm)
$l$:節点間長(mm)
異種強度梁の場合、補正したヤング係数 $E_{ce}$に、軸断面積 $A_n$を乗じて算定します。 補正ヤング係数は以下のように算出します。
$E_{ce}=E_{cu} \cdot T/D + E_{cd} \cdot (D-T)/D$ここで、
・
$E_{cu}=3.35 \cdot 10^4 \cdot (\gamma_u/24)^2 \cdot (F_{cu}/60)^{1/3}$ (単位:N/mm2)
・
$E_{cd}=3.35 \cdot 10^4 \cdot (\gamma_d/24)^2 \cdot (F_{cd}/60)^{1/3}$ (単位:N/mm2)
・
$\gamma_u$,
$\gamma_d$:それぞれ梁上部, 梁下部コンクリートの単位体積重量
・
$F_{cu}$,
$F_{cd}$:それぞれ梁上部, 梁下部コンクリート強度
せん断変形用断面積( $A_S$)
$A_s=\frac{B \cdot D}{\kappa}$$κ$:形状係数(=1.2)
異種強度梁の場合、補正したせん断弾性係数 $G_{ce}$に、せん断断面積 $A_s$(RESP-D計算編マニュアルに従います)を乗じて算定します。
異種強度梁のせん断弾性係数 $G_{ce}$は、補正したヤング係数 $E_{ce}$より下式により算定します。
$G_{ce}=E_{ce}/\{2(1+\nu)\}$断面2次モーメント( $I_e$)
鉄筋コンクリート造梁の断面2次モーメント( $I_e$)は鉄筋を考慮して次式により算定します。
$I_e = \frac{B \cdot D^3}{12}+ \frac{(b-B)t^3}{12}+B \cdot D \cdot (g-D/2)^2+(b-B) \cdot t \cdot (D-t/2-g)^2+(n_r-1) \sum \alpha_i(g-y_i)^2$ $g = \frac{1/2b \cdot D^2+(b-B) \cdot t \cdot (D-t/2)+(n_r-1) \sum \alpha_i \cdot y_i}{B \cdot D+(b-B) \cdot t+(n_r-1) \sum \alpha_i}$$g$:梁下端から図心位置までの距離(mm)
大梁で構造スラブにより異なるFcを指定した場合、以下の計算となります。
$I_e = \frac{B \cdot D^3}{12}+ \frac{(b-B)t^3}{12} \cdot \frac{E_s}{E_g} +B \cdot D \cdot (g-D/2)^2+(b-B) \cdot t \cdot (D-t/2-g)^2 \cdot \frac{E_s}{E_g} +(n_r-1) \sum \alpha_i(g-y_i)^2$$E_g$ : 大梁コンクリートヤング係数
$E_s$: スラブコンクリートヤング係数
異種強度梁の場合、補正したヤング係数 $E_{ce}$を用いて算定します。
ねじり断面2次モーメント( $J$)
指定により、ねじり剛性を考慮することが可能です。壁、床が取付かない元断面に対してねじり剛性を次式で算定します。
矩形 :
$J = \frac{B^3 \cdot D}{16} \cdot \left[ \frac{16}{3}-3.36 \cdot \frac{B}{D} \cdot \left( 1-\frac{1}{12} \cdot \left( \frac{B}{D} \right)^4 \right) \right]$円形 :
$J = \frac{\pi r^4}{2}$
RC柱
RC柱の剛性
剛性増大率
軸断面積
柱の軸断面積は袖壁および直交袖壁を考慮し、せん断断面積には直交袖壁は無視し袖壁のみ考慮します。袖壁のヤング係数は母材と同じと仮定します。
断面2次モーメント
柱の断面2次モーメントの算定方法は、下記のいずれかの選択により設定できます 注1)。 $A~C$を選択した場合は、直交壁は無視し、袖壁のみを評価して断面2次モーメントを求めます。求めた断面2次モーメントと元の断面の断面2次モーメントの比率を剛性増大率として設定します。
※「鉄筋・鉄骨の剛性を考慮する」とした場合には剛性増大率は変化せず、剛性増大率を乗じる元となる断面2次モーメントを増大させます。
RC柱の断面性能
鉄筋コンクリート造柱の断面性能の計算は以下によります。
軸断面積( $A_n$)
柱の軸断面積(An)は、鉄筋を考慮して次式により算定します。
$A_n = ({B \cdot (D-t)+B \cdot t+(n-1) \sum \alpha_i}) \cdot \frac{l_0}{l}$$n$:ヤング係数比
$l_0$:可撓長さ(剛域を考慮した長さ)(mm)
$l$:節点間長(mm)
せん断変形用断面積( $A_S$)
$A_s = \frac{B \cdot D}{\kappa}$$κ$:形状係数(=1.2)
断面2次モーメント( $I_e$)
鉄筋コンクリート造柱の断面2次モーメント( $I_e$)は鉄筋を考慮して次式により算定します。
$I_e = \frac{B \cdot D^3}{12}+ \frac{(b-B)t^3}{12}+B \cdot D \cdot (g-D/2)^2+(b-B) \cdot t \cdot (D-t/2-g)^2+(n_r-1) \sum \alpha_i(g-y_i)^2$ $g = \frac{1/2b \cdot D^2+(b-B) \cdot t \cdot (D-t/2)+(n_r-1) \sum \alpha_i \cdot y_i}{B \cdot D+(b-B) \cdot t+(n_r-1) \sum \alpha_i}$$g$:梁下端から図心位置までの距離(mm)
ねじり断面2次モーメント( $J$)
指定により、ねじり剛性を考慮することが可能です。壁、床が取付かない元断面に対してねじり剛性を次式で算定します。
矩形 :
$J = \frac{B^3 \cdot D}{16} \cdot \left[ \frac{16}{3}-3.36 \cdot \frac{B}{D} \cdot \left( 1-\frac{1}{12} \cdot \left( \frac{B}{D} \right)^4 \right) \right]$円形 :
$J = \frac{\pi r^4}{2}$
S大梁
S梁の剛性
断面積
梁の断面積は、角形鋼管のコーナー部分、H形鋼のフィレット部分などを考慮した実断面積とします。
合成梁の断面性能
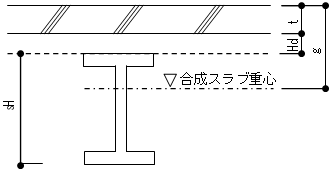
梁が合成梁の場合の断面性能を自動計算します。合成梁の剛性は、下式で求められるスラブを考慮した剛性と鉄骨梁のみの剛性の平均とします。
$g = \frac{_cE \cdot B \cdot t \cdot (t/2)+_sE \cdot _sA \cdot (t+Hd+_sH/2)}{_cE \cdot B \cdot t+_sE \cdot _sA}$ $I = \left( \frac{_cE}{_sE} \right) \cdot \left( \frac{B \cdot t^3}{12} +B \cdot t \cdot (g-t/2)^2 \right) +_sI+_sA \cdot (g-t-Hd-_sH/2)^2$ここで、
$_cE$ :コンクリートのヤング係数
$_sE$ :鋼材のヤング係数
$_sA$ :鋼材の断面積
$_sI$ :鋼材の断面2次モーメント
$t$ :スラブの厚さ(計算条件の剛性で入力した値)
$Hd$ :デッキ高さ(計算条件の剛性で入力した値)
断面欠損の考慮
(フランジ)
継手部の断面欠損を考慮する場合、ユーザー指定の低減値によりフランジ幅を低減します。
(ウェブ)
継手部およびスカラップによる断面欠損を考慮する場合には、ユーザー指定の低減値によりウェブ板厚を一律に低減します。
S大梁の断面性能
軸断面積( $A_n$)
柱・梁の軸断面積( $A_n$)は、次式により算定します。
$A_n=A$$A$:鉄骨全断面積( $mm^2$)
せん断変形用断面積( $A_S$)
$A_s=\frac{A_w}{\kappa}$$κ$:形状係数(=1.0)
断面2次モーメント( $I$)
H形 : $I = \frac{BH^3-(B-t_w)(H-2t_f)^3}{12}$
角型鋼管 : $I = \frac{BH^3-(B-2t_w)(H-2t_f)^3}{12}$
円形鋼管 : $I = \frac{\pi (D^4-d^4)}{64}$
$H$ :鉄骨梁せい (mm)
$B$ :フランジ幅 (mm)
$t_f$ :フランジ厚 (mm)
$t_w$ :ウェブ厚 (mm)
ねじり断面2次モーメント( $J$)
指定により、ねじり剛性を考慮することが可能です。
H形 : $J = \frac{1}{3} \left( 2 \cdot B \cdot t_f^3+(H-2 \cdot t_f) \cdot t_w^3 \right)$
S柱
S柱の剛性
断面積の考え方
柱の断面積は、角形鋼管のコーナー部分、H形鋼のフィレット部分などを考慮した実断面積とします。
断面欠損の考慮
(フランジ)
継手部の断面欠損を考慮する場合、ユーザー指定の低減値によりフランジ幅を低減します。
(ウェブ)
継手部およびスカラップによる断面欠損を考慮する場合には、ユーザー指定の低減値によりウェブ板厚を一律に低減します。
S柱の断面性能
軸断面積( $A_n$)
柱の軸断面積(An)は、次式により算定します。
$A_n = A$$A$:鉄骨全断面積(mm2)
せん断変形用断面積( $A_s$)
$A_s = \frac{A_w}{\kappa}$$κ$:形状係数(=1.0)
断面2次モーメント( $I$)
H形 : $I = \frac{BH^3-(B-t_w)(H-2t_f)^3}{12}$
角型鋼管 : $I = \frac{BH^3-(B-2t_w)(H-2t_f)^3}{12}$
円形鋼管 : $I = \frac{\pi (D^4-d^4)}{64}$
$H$ :鉄骨梁せい (mm)
$B$ :フランジ幅 (mm)
$t_f$ :フランジ厚 (mm)
$t_w$ :ウェブ厚 (mm)
ねじり断面2次モーメント( $J$)
指定により、ねじり剛性を考慮することが可能です。
H形 : $J = \frac{1}{3} \left( 2 \cdot B \cdot t_f^3+(H-2 \cdot t_f) \cdot t_w^3 \right)$
角型鋼管 : $J = \frac{2t_ft_w(B-t_f)^2(H-t_w)^2}{Bt_w+Ht_f-t_f^2-t_w^2}$
円形鋼管 : $J = \frac{ \pi (D^4-d^4)}{32}$ ( $D$ : 外径、 $d$ : 内径 )
CFT : $J = \frac{_sG}{_cG} {_s}J+_cJ$ (※コンクリートのせん断弾性係数を乗じて剛性とする)
SRC大梁
SRC造梁の剛性
断面性能はRC造梁の剛性とS梁の剛性に対し、下記計算式によりヤング係数比およびせん断弾性係数比を考慮して累加した値を用います。
SRC梁の断面性能
軸断面積( $A_n$)
梁の軸断面積( $A_n$)は次式により算定します。
$A_n = _{rc}A_n+_sA_n(n_s-1)$$_{rc}A_n$ :RC部分の軸断面積
$_sA_n$ :S部分の軸断面積
$n_s$ :鉄骨のヤング係数比
せん断変形用断面積( $A_S$)
$A_s$ = ( $_{rc}A_s$ + $_sA_s(n _{gs}-1$))
$_{rc}A_s$ :RC部分のせん断断面積
$_sA_s$ :S部分のせん断断面積
$_ng_s$ :鉄骨のせん断弾性係数比
断面2次モーメント( $I_e$)
梁の断面2次モーメント( $I_e$)は次式により算定します。
$I_n$ = ( $_{rc}I_e$ + $_sI_e(n_s-1$))
$_{rc}I_e$ :RC部分の軸断面積
$_sI_e$ :S部分の軸断面積
$n_s$ :鉄骨のヤング係数比
ねじり断面2次モーメント( $J$)
指定により、ねじり剛性を考慮することが可能です。
SRC : $J = \frac{_sG}{_cG} {_s}J+_cJ$ (※コンクリートのせん断弾性係数を乗じて剛性とする)
SRC柱
SRC柱の剛性
断面性能はRC造柱の剛性とS柱の剛性に対し、下記計算式によりヤング係数比およびせん断弾性係数比を考慮して累加した値を用います。CFTもこれに準じます。
SRC梁の断面性能
軸断面積( $An$)
柱の軸断面積( $An$)は次式により算定します。
$A_n = _{rc}A_n+_sA_n(n_s-1)$$_{rc}A_n$ :RC部分の軸断面積
$_sA_n$ :S部分の軸断面積
$n_s$ :鉄骨のヤング係数比
せん断変形用断面積( $A_S$)
$A_s$ = ( $_{rc}A_s$ + $_sA_s(n _ {gs}-1$))
$_{rc}A_s$ :RC部分のせん断断面積
$_sA_s$ :S部分のせん断断面積
$_ng_s$ :鉄骨のせん断弾性係数比
断面2次モーメント( $I_e$)
柱の断面2次モーメント(Ie)は次式により算定します。
$I_n = _{rc}I_e+_sI_e(n_s-1)$$_{rc}I_e$ :RC部分の軸断面積
$_sI_e$ :S部分の軸断面積
$n_s$ :鉄骨のヤング係数比
ねじり断面2次モーメント( $J$)
指定により、ねじり剛性を考慮することが可能です。
SRC : $J = \frac{_sG}{_cG} {_s}J+_cJ$ (※コンクリートのせん断弾性係数を乗じて剛性とする)
非充複SRC大梁・柱
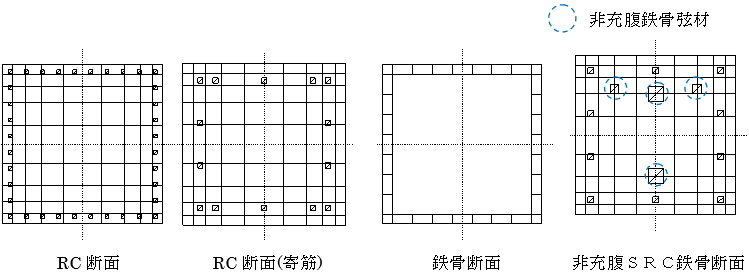
非充腹SRC造柱・梁の剛性
断面性能はRC造柱・梁の剛性と非充腹鉄骨弦材の剛性に対し、下記計算式によりヤング係数比を考慮して累加した値を用います。
$A = _rA+(n-1)×_sA$ $A_s = _rA_s$ $I = _rI+(n-1)×_sI$$A$ :非充腹SRC断面積
$A_s$ :非充腹SRCせん断断面積
$I$ :非充腹SRC断面2次モーメント
$_rA$ :RC断面積
$_rA_s$ :RCせん断断面積
$_rI$ :RC断面2次モーメント
$_sA$ :非充腹鉄骨弦材断面積
$_sI$ :非充腹鉄骨弦材断面2次モーメント
$n$ :ヤング係数比
間柱ダンパーの剛性
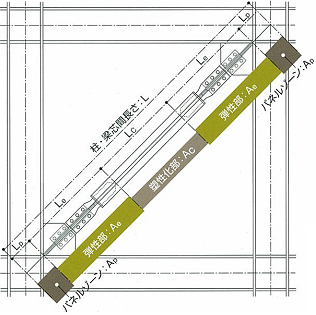
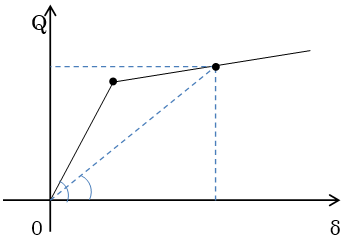
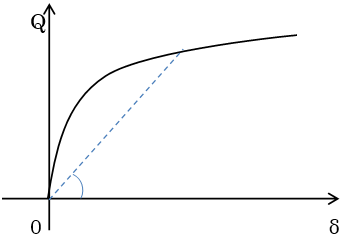
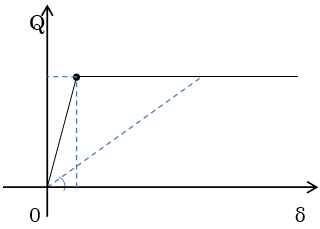
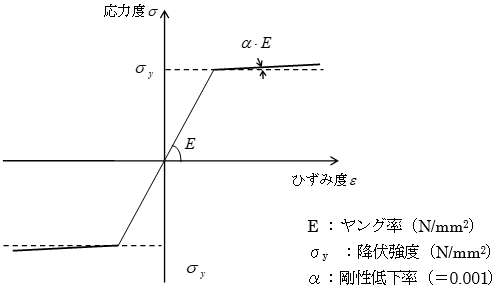
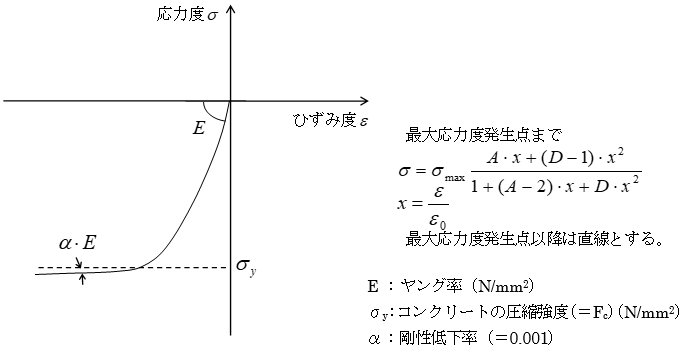
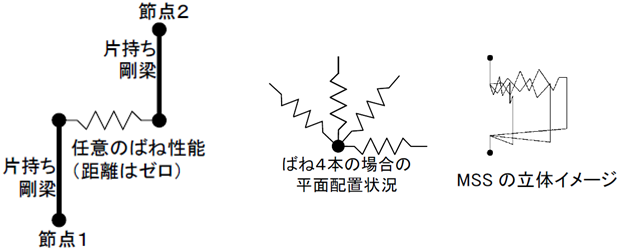
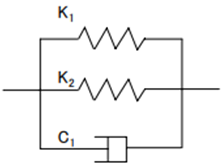
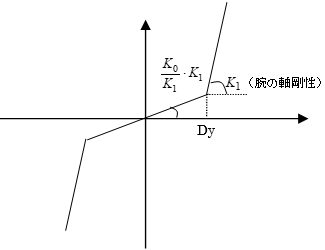
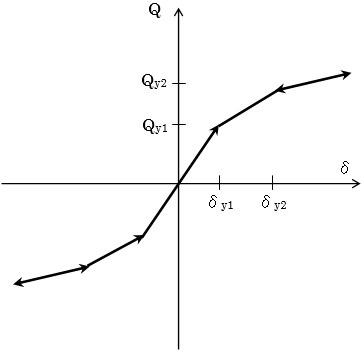
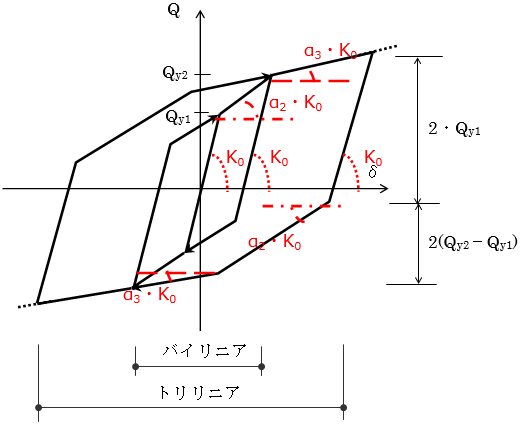
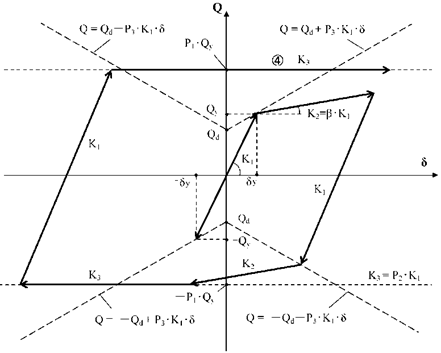
間柱ダンパーは支持部とダンパー部からなる3分割要素としてモデル化されます。支持部、ダンパー部それぞれ異なる剛性として評価します。ダンパー部は製品の特性により、履歴型の非線形特性を有するものとしてモデル化します。支持部の長さは下図のように算出されます。ダンパーの種類により、静的剛性を持つもの、静的剛性を持たないもの、指定により静的剛性を考慮することが可能なものがあります。
| 種別 | 種類 | 静的剛性 |
|---|---|---|
| 履歴型 | 間柱型鋼材ダンパー | あり |
| JFEシビル制振間柱 | あり | |
| 粘性・粘弾性 | オイレス工業粘性制震壁 | 指定により考慮可 |
| 免制振ディバイス粘性制震壁 | なし | |
| 日鉄エンジニアリング | あり | |
| ユニットゴムダンパー | ||
| 住友理工 TRCダンパー | あり | |
| AFTダンパーシステム | なし | |
| JFEシビル間柱型粘弾性ダンパー | 指定により考慮可 | |
| コンステック CSTダンパー | なし | |
| 流体 | オイルダンパー | なし |
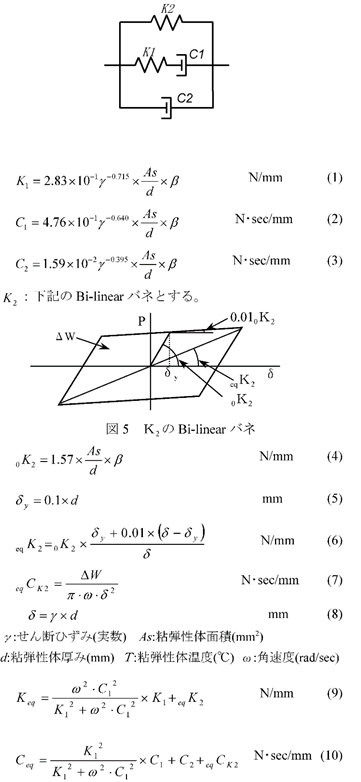
日鉄エンジニアリングユニットゴムダンパーの静的弾性剛性
静的弾性解析時の剛性は、以下の式に対しγ=0.1、β=20.0を代入して算出したkuを用います。
a) 等価剛性 keq(kN/mm)
$k_{eq} = G_{eq}\times\frac{s}{d}$$G_{eq}$:等価せん断弾性係数( $kN/mm^2$)
$G_{eq}$= $0.84×γ^{-0.5}$ ( $0.1≦γ≦3.0$)
$γ$:歪み $s$:せん断面積( $mm^2$) $d$:厚さ( $mm$)
b) 一次剛性 ku(kN/mm)
$k_u = \beta \times k_{eq}$
住友理工 TRCダンパーの静的剛性
静的弾性解析時の剛性は、以下の式により計算します。
$_0K_2 = 1.57\times\frac{As}{d}\times\beta$$β$: 温度補正係数 (= $e^{-0.017(T-20)}$)
耐震壁(壁エレメントモデル)の剛性
耐震壁(壁エレメントモデル)の断面性能
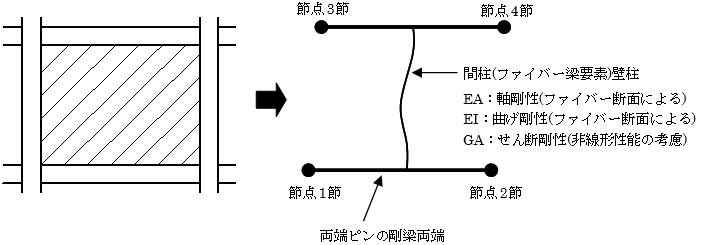
耐震壁は壁エレメントモデルでモデル化されます(指定により、平面応力要素、板要素でモデル化することも可能です)。全体としての断面性能は、壁柱の断面性能、側柱の断面性能および上下大梁の断面性能により表現されます。
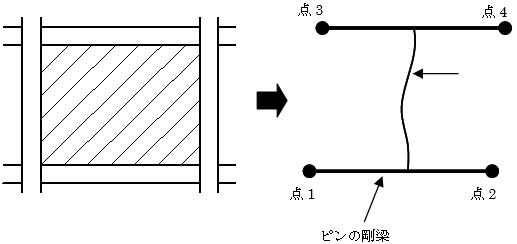
壁エレメントモデルは、鉛直の梁要素(間柱)を両端ピンの剛梁ではさみ込んでモデル化し、剛梁と間柱は剛接合、剛梁の両端はピン接合となっています。このため、四隅の節点の水平・上下の変形が間柱に伝達されます。なお、剛梁は実際に梁要素が存在するわけではなく、剛域変換によって剛梁の両端の節点の変位が間柱に伝達されます。
壁柱の断面性能
軸剛性 :壁板部分の断面積から計算します(鉄筋剛性を考慮します)
曲げ剛性 :壁板部分の断面にもモーメントから計算します(鉄筋剛性を考慮します)
側柱部分のローカル断面2次モーメントは考慮しません。
せん断剛性 :壁板部分の断面および側柱部分の断面から計算します。
その際、下式による形状係数および開口による低減率rを考慮します。
$\kappa = \frac{3(1+\xi)}{5(1-\xi^3(1-\eta))^2} \left[\eta+\xi(1-\eta) \left( \frac{15}{8}(1-\xi^2)^2-\xi^4\eta \right) \right]$ $r = 1-1.25 \sqrt{ \frac{h_0 \cdot l_0}{h \cdot l}}$側柱の断面性能
軸剛性 :通常の柱と同様に計算します。
曲げ剛性 :通常の柱と同様に計算します。
ただし、耐震壁面内方向は両端ピンのためモーメントを負担しません。
せん断剛性 :通常の柱と同様に計算します。
ただし、耐震壁面内方向は両端ピンのためせん断力を負担しません。
上下大梁の断面性能
通常の大梁に対し、倍率を乗じた剛性を採用します。倍率は剛性計算条件で設定できます。既定値は100倍となります。
耐震壁の判定
耐震壁の条件は下記を満たすものとして取り扱います。ただし、下記によらず強制的に耐震壁とみなして壁エレメントモデルとしてモデル化する指定も可能です。
- スリットがないこと。
- 壁厚が120mm以上であること。
- 開口周比r0≦0.4を満たすこと。
(指定によりL0/L、H0/Hも条件に含めることが可能です)
複数開口の取り扱い
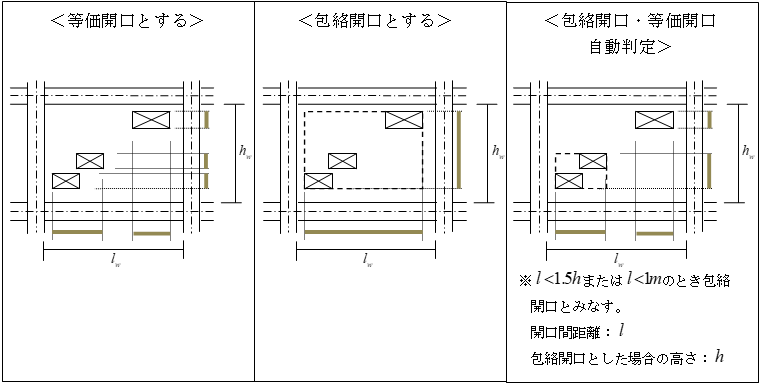
複数の開口部については、「等価開口とする」「包絡する」「包絡開口・等価開口自動判定」の3つから選択できます。それぞれ下記のように開口を評価します。なお、3つ以上の開口があり「包絡開口・等価開口自動判定」とした場合、各開口間で包絡開口が作れなくなるまで繰り返し包絡開口を作成し、包絡できなくなった時点の開口状況で「等価開口とする」と同様の判定を行います。
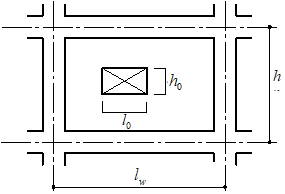
$l_w$:壁内法幅
$h_w$:壁内法高さ
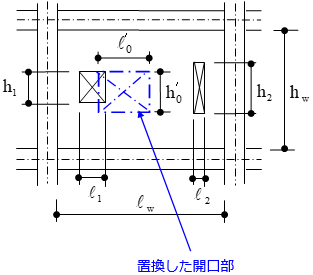
また、等価開口とする場合の開口寸法は以下のように計算します。
$l'_0\times h'_0=l_1\times h_1+l_2\times h_2$ $l'_0:h'_0=l_w:h_w$$h_1,h_2$ :開口部の高さ
$l_1,l_2$ :開口部の長さ
$h_w$ :壁の内法高さ
$l_w$ :壁の内法長さ
$h'_0$ :置換した開口部の高さ
$l'_0$ :置換した開口部の長さ
フレーム内雑壁のモデル化
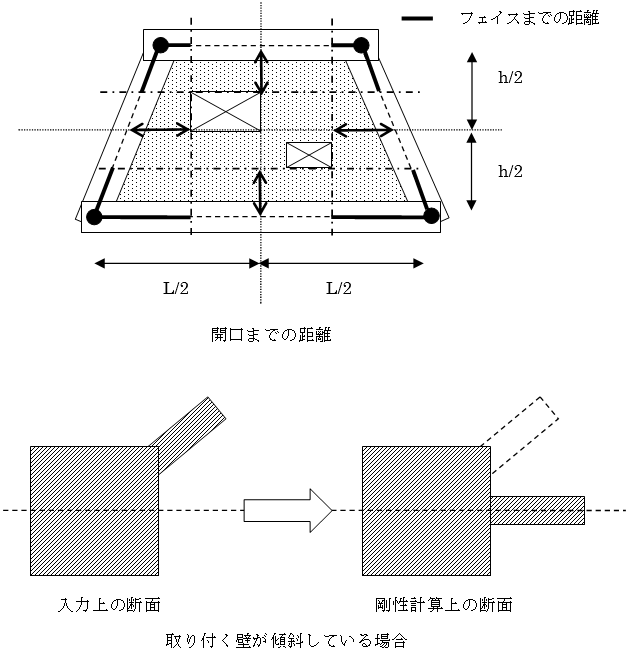
壁が開口により耐震壁にならなかった場合、周辺のRC部材およびSRC部材の断面性能に壁が考慮されます。複数開口が存在する場合は、包絡開口により壁の長さを考慮します。剛性に用いる壁の長さは構造階高および軸間距離の1/2の位置における包絡開口までの距離を採用します。また、柱の回転により壁が傾斜して部材に取り付いている場合には傾斜を無視し軸上に壁断面があるものとして計算します。
開口の位置は意匠階高を基準として算出します。 上下の梁が鉛直方向に傾き、下層節点または上層節点においてZ座標が異なる場合は、以下のように認識します。
- 上層節点は、Z座標の小さい方を基準にします。
- 下層節点は、Z座標の大きい方を基準にします。
耐震壁(平面応力要素、板要素)の断面性能
指定により、耐震壁を平面応力要素および板要素としてモデル化することが可能です。
面要素は節点位置に対して配置されます。
面要素でモデル化した場合、付帯柱はピンとなりません。
また、指定により周辺の柱梁および面要素をメッシュ分割することが可能です。
ブレースの剛性
一般ブレースの剛性
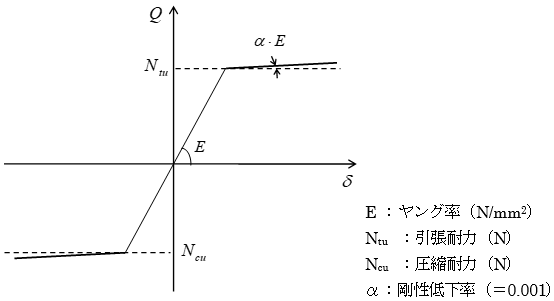
一般ブレースの剛性計算は、下式によって求めます。 引張専用ブレースとした場合、引張となるブレースと圧縮となるブレースが対になって存在すると考え、弾性解析では剛性を1/2としてモデル化します。弾塑性解析の場合は初期剛性は1倍としてモデル化されます。
$K_B = \frac{EA}{L}$
ここで、
$L$:芯々間の長さ
$A$:降伏部の断面積
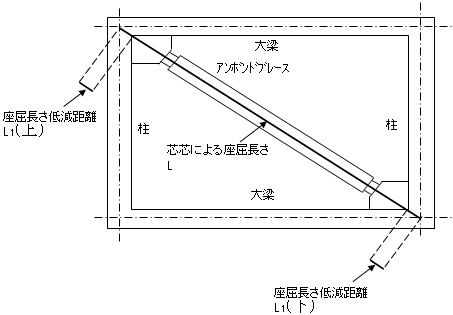
日鉄エンジニアリングアンボンドブレースの剛性
アンボンドブレースの1次剛性は下式により計算します。
$K_1 = \phi_A\times \frac{EA_c}{L}$
$φ_A$:等価剛性倍率
$L$:芯芯間の長さ
$A_c$:塑性化部断面積
等価剛性倍率の計算例を以下に示します。
$\phi_A = \frac{1}{\alpha+2\beta \frac{A_c}{A_e}+(1-\alpha-2\beta ) \frac{A_c}{A_p}}$
ここで、
$α$ :塑性化部長さの柱・梁芯間長さに対する比(= $L_c/L$)
$β$ :弾性部長さの柱・梁芯間長さに対する比(= $L_e/L$)
$A_c/A_e$ : 塑性化部断面積の弾性部断面積に対する比
$A_c/A$p$ : 塑性化部断面積のパネルゾーン断面積に対する比
JFEシビル KTブレースの剛性
JFEシビルKTブレースの剛性計算は下式によって求めます。
$K_B = \frac{EA}{L}$ ここで、
$L$:構造心間長さ
$A$:軸力管の断面積
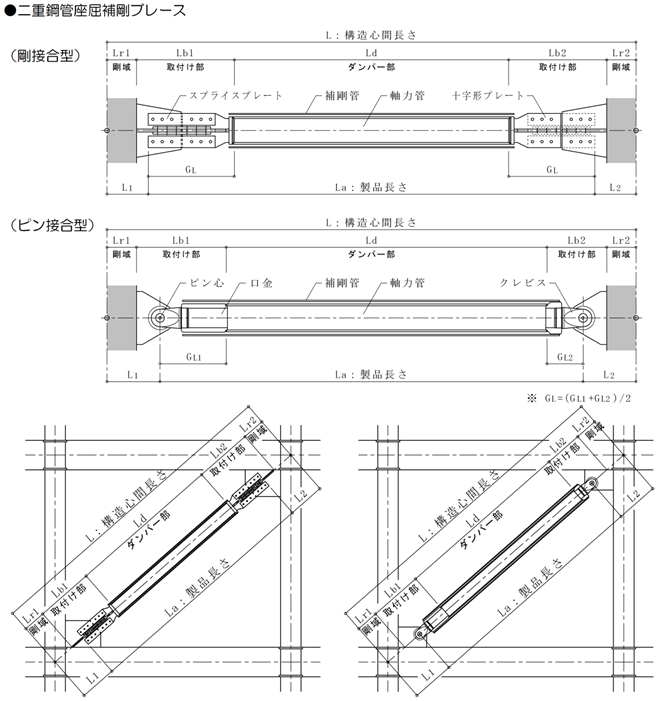
JFEシビル 二重鋼管座屈補剛ブレースの剛性
JFEシビル二重鋼管座屈補剛ブレースの剛性計算は以下によって求めます。
剛性計算を「自動」とした場合、JFEシビル二重鋼管座屈補剛ブレースの剛性計算は下式によって求めます。
$\frac{1}{K_e} = \frac{1}{K_d}+\frac{1}{K_b}+\frac{1}{K_r}, \quad K_d = \frac{E \cdot A_d}{L_d}, \quad K_b = \frac{b \cdot E \cdot A_d}{L_b}, \quad K_r = \frac{E \cdot A_r}{L_r} = \infty$$K_e$ : ブレース剛性
$K_d$ : ダンパー部剛性
$K_b$ : 取付け部剛性
$K_r$ : 剛域部剛性
$b : 取付け部断面積比(=$A_b/A_d$)
$L_d$ : ダンパー部長さ
$L_b$ : 取付け部長さ
$L_r$ : 剛域部長さ
$A_d$ : ダンパー部
$A_b$ : 取付け部断面積
$A_r$ : 剛域部断面積(=∞)
ダンパー部長さ、取付け部長さを以下のように計算します。
$L_d = d \cdot L, \quad L_b = (1-d-r) \cdot L, \quad L_r = L-L_d-L_r$$d$ : ダンパー部長さ
$r$ : 剛域部長さ
$L$ :構造芯間長さ
ダンパー部長さ比、剛域長さ比は以下のように計算します。
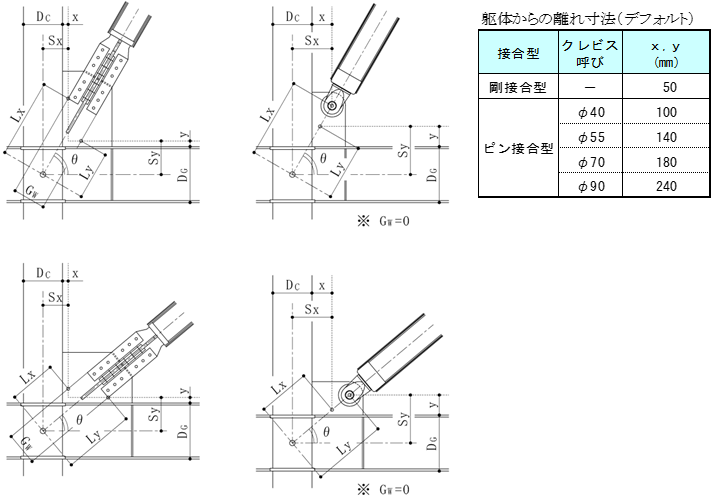
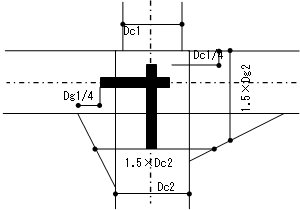
$d = 1-\frac{\max (L_{x1},L_{y1})+\max (L_{x2},L_{y2}) +2 \cdot G_L}{L}$ $L_{x1} = S_{x1}/ \cos \theta+0.5 \cdot G_w \cdot \tan \theta$ $L_{y1} = S_{y1}/ \sin \theta+0.5 \cdot G_w/ \tan \theta$ $S_{x1} = 0.5 \cdot D_{C1}+x1$ $S_{y1} = 0.5 \cdot D_{G1}+y1$ $L_{x2} = S_{x2}/ \cos \theta+0.5 \cdot G_w \cdot \tan \theta$ $L_{y2} = S_{y2}/ \sin \theta+0.5 \cdot G_w/ \tan \theta$ $S_{x2} = 0.5 \cdot D_{C1}+x2$ $S_{y2} = 0.5 \cdot D_{G1}+y2$ $r = \frac{\max (R_{x1},R_{y1})+\max (R_{x2},R_{y2})}{L}$ $R_{x1} = 0.5 \cdot D_{C1}/ \cos \theta$ $R_{y1} = 0.5 \cdot D_{G1}/ \sin \theta$ $R_{x2} = 0.5 \cdot D_{C2}/ \cos \theta$ $R_{y2} = 0.5 \cdot D_{G2}/ \sin \theta$剛性計算を「倍率指定」とした場合、JFEシビル二重鋼管座屈補剛ブレースの剛性計算は下式によって求めます。
$K_e = \alpha \cdot K_d, \quad K_d = \frac{E \cdot A_d}{L}$$L$ : 構造芯間長さ
$K_e$ : ブレース剛性
$K_d$ : ダンパー部合成
$α$ : 指定倍率
免震支承材の剛性
静的・動的解析モデルの剛性
免震部材の剛性は各メーカーカタログスペックによります。
モデル化は「応力計算条件」の「免震部材のモデル化」によって変わります。
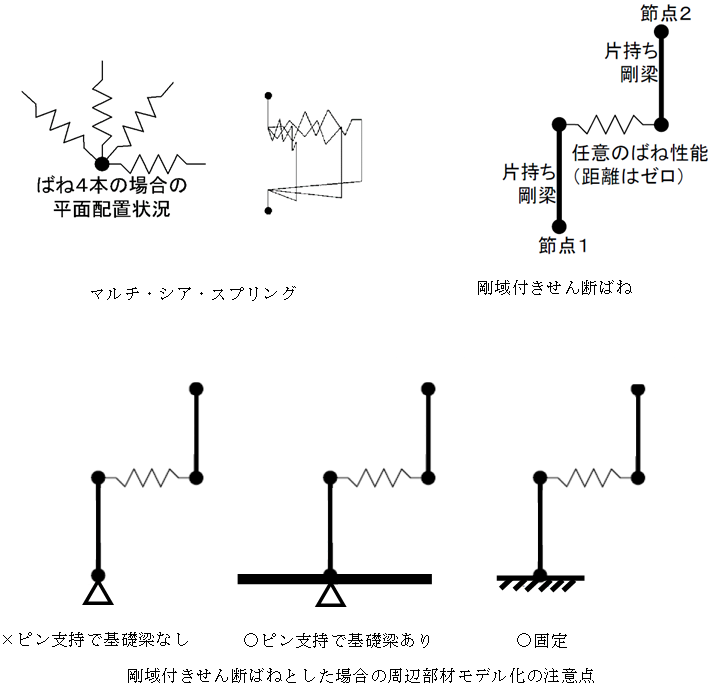
「せん断力によって生じるモーメントを伝達する」とした場合、免震部材は下図に示す「剛域付きせん断ばね」でモデル化されます。このモデル化とした場合、免震部材上下の節点は回転に対する抵抗力を有しないと不安定となります。
「せん断ばねによって生じるモーメントを伝達しない」とした場合、免震部材は「せん断ばね」としてモデル化され、免震部材の上下の階にモーメントを伝達しません。
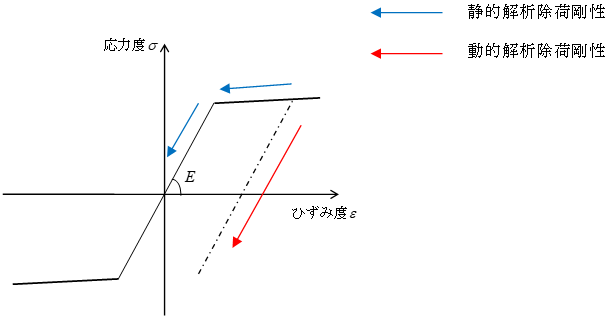
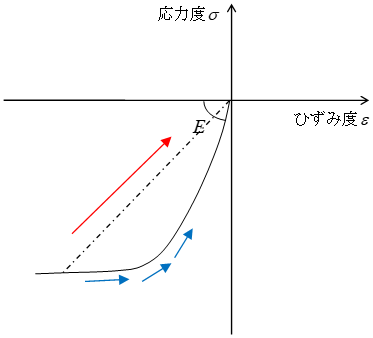
なお、免震部材の静的解析時剛性は、「剛性条件」「静的解析時の免震部材剛性」の設定により変わります。「静的解析時には免震部材を固定する」とした場合、せん断剛性を剛としてモデル化し、振動解析の時のみ本来のせん断剛性を採用して計算します。
また、ばねの部分は積層ゴム支承や履歴系減衰材の場合はマルチ・シア・スプリングでモデル化します。すべり支承の場合は動的解析においては方向ごとではなくベクトルによる合力で滑り状態を評価する摩擦ばねでモデル化されますが、静的解析時にはマルチ・シア・スプリングでモデル化します。
静的解析時の剛性については、デフォルトでは十分に硬い剛性となるような剛性倍率を乗じてモデル化されます。倍率については「剛性計算条件」で指定可能です。
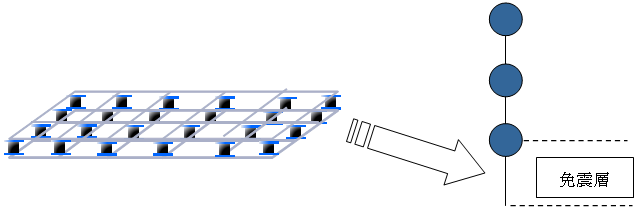
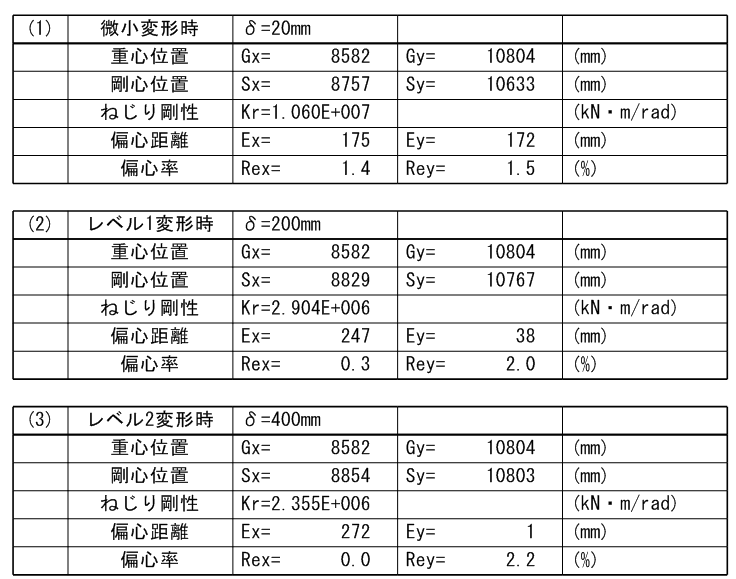
免震層偏心率計算・固有値解析モデルの剛性
免震構造では、免震層の変形を仮定した割線剛性によるせん断剛性から偏心率計算および固有値解析を行うことができます。仮定する変形は、「免震層設計条件」により設定します。なお、免震構造として認識させるためには「基本事項」→「階・軸の追加・削除」→「階名称の変更・免震層指定」により免震層を設定する必要があります。
鉛プラグ挿入型積層ゴム、錫プラグ挿入型積層ゴム、
U型ダンパー e.t.c.
(バイリニアもしくは歪み依存バイリニアとなる部材)
高減衰積層ゴム e.t.c.
(曲線的な挙動となる部材)
弾性すべり支承、転がり支承 e.t.c.
(完全バイリニアとなる部材)
剛域の計算
RC造・SRC造の剛域(自動計算)
柱・梁の剛域は、壁が取り合わない場合と取り合う場合、また壁が取り合わない場合については梁にハンチがある場合とない場合を考慮します。耐震壁周辺の柱・梁の剛域は考慮しません。剛域長さは柱・梁毎に個別に指定することができます。
1. 壁が取り合わない場合(梁ハンチなし)
柱・梁フェイスからそれぞれの部材せいの1/4だけ内側に入った位置(指定により変更可)を剛域とします。
2. 壁が取り合わない場合(梁ハンチあり)
材が軸に対し25°以上の傾斜をするハンチを持つ場合には、材のせいが1.5倍の点を持って剛域を 定めます。ただし、ハンチの傾斜が60°以上のときは、ハンチの基点より材せいの1/4入った点 (指定により変更可)で 定めます。左右のハンチの差異、その他によって 上に定めた点が2点以上同時に存在する場合には 剛とみなせる部分が大きい方によります。
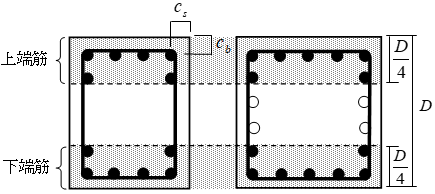
3. 腰壁・垂壁・袖壁が取りつく場合(梁ハンチなし)
腰壁・垂壁・袖壁が取りつく場合、下記のように剛域を設定します。入り長さ計算用のせいはフレーム内雑壁を含んだせいとします。
4. 腰壁・垂壁・袖壁が取りつく場合(梁ハンチあり)
2、3による剛域のいずれか大きい方を取ります。
S造の剛域(自動計算)
剛域長さは0とします(指定により入り長さを設定することも可能)。
危険断面位置はフェイスとします。
混合構造の剛域(自動計算)
混合構造の場合の剛域は下記のルールで設定します。
RC・SRC柱の場合
仕口部に接続する大梁にRC・SRC大梁が存在する場合、RC・SRC大梁のうち最大せいの梁フェイスからD/4内側(指定によります)までの長さを剛域長さとします。
仕口部に接続する大梁がすべてS大梁の場合、剛域長さは0とします(入り長さで剛域を指定した場合には指定した入り長さから計算されます)。
S柱の場合
仕口部に接続する大梁にRC・SRC大梁が存在する場合、RC・SRC大梁のうち最大せいの梁フェイスまでの長さを剛域長さとします。
仕口部に接続する大梁がすべてS大梁の場合、剛域長さは0とします(入り長さで剛域を指定した場合には指定した入り長さから計算されます)。
RC・SRC大梁の場合
仕口部に接続する柱にRC柱が存在する場合、RC・SRC柱のうち最大せいの柱フェイスからD/4内側(指定によります)までの長さを剛域長さとします。
仕口部に接続する柱がすべてS柱の場合、剛域長さは0とします(入り長さで剛域を指定した場合には指定した入り長さから計算されます)。
S大梁の場合
仕口部に接続する柱にRC・SRC柱が存在する場合、RC・SRC造柱のうち最大せいの柱フェイスまでの長さを剛域長さとします。
仕口部に接続する大梁がすべてS柱の場合、剛域長さは0とします(入り長さで剛域を指定した場合には指定した入り長さから計算されます)。
仕口パネルの計算
剛域・材端ばねとの関連性
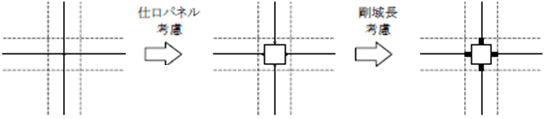
仕口パネルと剛域を同時に設定した場合には、パネルからはみ出した部分を剛域として計算します。RCおよびSRCの場合には剛性条件で仕口パネルを指定した場合、仕口パネルと剛域が自動的に設けられます。また、Sで仕口パネルを指定した場合でも、剛域を直接入力した場合には仕口パネルと剛域が設けられます。
また、材端ばね、材端ピンを設定した場合、ピン位置は仕口パネルまたは剛域の長い方の端部に接続します。
RC造・SRC造の仕口パネル
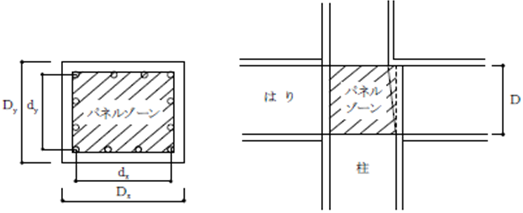
RCあるいはSRCパネルゾーン(接合部)の大きさは下記のように設定されます。
幅 :下層階柱の最大端主筋間距離
せい :取りつく最大せい梁の最外端主筋間距離
S造の仕口パネル
Sパネルゾーン(接合部)の大きさは下記のように設定されます。
幅 :下層階柱の鉄骨形状幅
せい :取りつく最大せい梁の鉄骨形状せい
また、パネルゾーンの厚さは柱のウェブ厚とします。ただし、BOX柱の場合にはウェブ厚の2倍とします。CFTの場合、コンクリート断面と鉄骨断面を等価なせん断剛性を持つコンクリート断面として置換して用います。
混合接合部
柱RC,大梁Sのような混合接合部の場合、仕口パネルは考慮せず剛域が考慮されます。
仕口パネルのサイズと諸元
仕口パネルのサイズは以下のように計算されます。
| RC | SRC | S | CFT | |
|---|---|---|---|---|
| せん断パネル幅 | B-2×dt | B-2×dt | ウェブ厚さ | RC断面とした場合の等価幅 |
| せん断パネル長さ | D-2×dt | D-2×dt | ウェブ長さ | ウェブ長さ |
| 材料定数 | RC | RC | S | RC |
その他
雑壁の剛性
フレーム内雑壁の剛性は柱の剛性として考慮します。フレーム外雑壁の剛性は、長期、水平荷重時、荷重増分解析時および立体振動解析時には考慮しません。ただし、偏心率の計算において剛性を考慮した結果も算出します。
03. 応力解析
03. 応力解析のサブセクション
応力解析モデル
応力解析モデル
解析モデルの概要
応力及び変位は、各荷重ケースについて、3次元立体解析モデルによる応力解析を行うことにより算出します。なお、長期応力解析においては、計算条件の指定により以下の部材について長期軸力を負担させないことも可能です。
- ブレース
- 柱、制振間柱
応力解析の変形の考慮
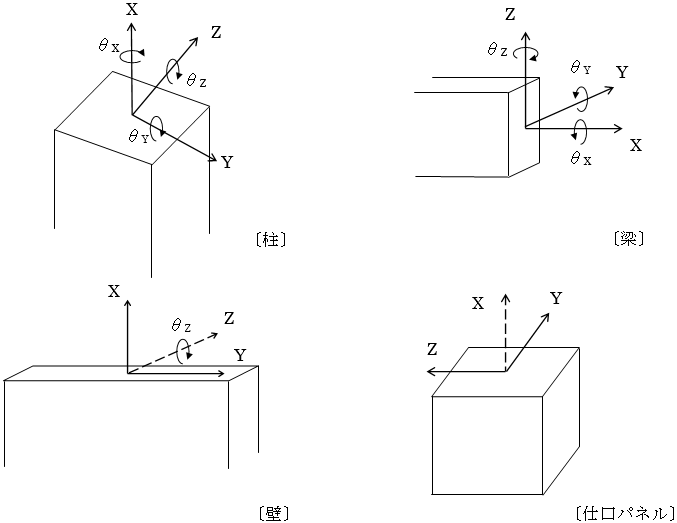
各部材の変形は、下表に示す成分について考慮します。
部材の変形と自由度
| 曲げ変形 | せん断 | |||||
|---|---|---|---|---|---|---|
| 部位・部材 | θX | θY | θZ | γY | γZ | δX |
| 柱 | ○*1 | ○ | ○ | ○ | ○ | ○ |
| 梁 | ○*1 | ○ | ○ | ○ | ○ | ○ |
| 壁 | ― | ― | ○ | ○ | ― | ○ |
| ブレース | ― | ― | ― | ― | ― | ○ |
| 節点バネ | ― | ○ | ○ | ○ | ○ | ○ |
| 仕口パネル | ― | ― | ― | ○ | ○ | ― |
部材の変形と自由度
層間変形角、剛性率
層間変形角、剛性率
立体として応力解析を行うため、層間変形角は位置ごとに異なります。層間変形角は、その階の柱の層間変形角の最大値を用いて確認します。ただし、斜め柱の変形角は除外します。
$$\frac{1}{_i r_s} = \frac{ \max (_i \delta 1, \quad _i \delta 2, \cdots _i \delta n)}{_i H} < \frac{1}{120}$$$δ$ :柱頭の変位-柱脚の変位(地震力の方向の水平変位)
$n$ :柱本数
$H$ :階高
$r_s$ :層間変形角の逆数
$i$ :階を示す添字
剛性率 $R_s$の計算式を以下に示します。ただし、剛性率算出時の層間変形角 $_i r_s$は、下式で行います。
$$\frac{1}{_i r_s} = \frac{i \delta g}{_i H}$$ $_i R_s = \frac{_i r_s}{r_s} \verb|≧| 0.6$$_i δ_g$:重心位置の層間変位
$r_s$: $_i r_s$の相加平均( $\frac{\Sigma _i r_s}{N}$)
$N$:階数
層間変形角・剛性率(階数分計算)
偏心率
偏心率
偏心率 $R_e$の計算式を以下に示します。
$$ R_e = \frac{e}{r_e} \leqq 0.15$$$e$ :偏心距離(mm)
$r_e$:弾力半径(mm)
偏心率を計算するために、階ごとに重心、剛心を求めます。
(1) 重心
各階の重心は、鉛直荷重を支持する柱の長期荷重による軸力Nおよびその部材の平面座標から計算します。
$$g_x = \frac{\sum(N_i \cdot x_i)}{\sum N_i}$$ $$g_y = \frac{\sum(N_i \cdot y_i)}{\sum N_i}$$(i:柱番号)
(2) 剛心
剛心は、その階の柱の水平方向剛性の中心として求めます。各柱の水平剛性は、地震時応力解析結果のせん断力と層間変位により計算します。
水平方向に対する剛性は、水平荷重時の応力と変位を用いて計算します。
$$k_i = \frac{Q_i}{\delta _i}$$ $$l_x = \frac{\sum(k_{Y_i} \cdot x_i)}{\sum k_{Y_i}}$$ $$l_y = \frac{\sum(k_{X_i} \cdot y_i)}{\sum k_{X_i}}$$(i:柱番号)
(3) 偏心距離 $e$
偏心距離は、重心及び剛心の座標から次式のように計算されます。
$$e_x = |l_x-g_x| , e_y = |l_y-g_y|$$(4) ねじり剛性
剛心周りのねじり剛性を各階毎に1つ求めます。剛心周りに計算を行うので、座標の平行移動により剛心を座標原点とします。新しい座標系を $\overline{X_i}-\overline{Y_i}$ とすれば、各柱の座標は、
$$\overline{X_i} = X_i-l_x , \overline{Y_i} = Y_i-l_y$$となります。各柱の剛性は、座標変換による変更はしません。剛心周りのねじり剛性KRは、
$$K_R= \Sigma (K_{X_i} \cdot \overline{Y_i}^2)+ \Sigma (K_{Y_i} \cdot \overline{X_i}^2)$$により求めます。Σは、X方向及びY方向それぞれについての耐震要素の和をとります。
(5) 弾力半径 $r_e$
$r_e$は弾力半径です。X,Y方向検討時のものをそれぞれ $r_{e_x}$, $r_{e_y}$とすると、
$$r_{e_x} =\frac{ \sqrt{K_R}} {\sum K_{X_i}},r_{e_y} =\frac{ \sqrt{K_R}}{ \sum K_{Y_i} }$$となります。
(6) Reの計算
X,Y各方向に対する偏心率をそれぞれ $R_{e_x}$、 $R_{e_y}$とすると、
$$R_{e_x} = \frac{e_y}{r_{e_x}}, R_{e_y} = \frac{e_x}{r_{e_y}}$$となります。
(7) 雑壁の剛性評価
剛性率・偏心率を求める際、雑壁の剛性 $K_w$は、n倍法にて計算されます。 次式により雑壁の剛性を $K_w$’求めます。
$$K_w' = n \cdot A_w' \cdot \frac{\Sigma K_c}{\Sigma A_c}$$ここで $A_w'$:雑壁の断面積
$\Sigma A_C$:当該階の柱の断面積の和
$\Sigma K_C$:当該階の柱の剛性の和
$n$ :雑壁の剛性を柱の剛性から求める場合の係数で、入力した値
ただし、 $\Sigma A_C$が0の場合は、 $\Sigma K_w'$を0とします。
偏心率の計算は常に弾性解析結果から計算されます。応力解析条件で「許容応力度計算時の応力解析方法」を「弾塑性解析結果」とした場合にも弾性解析の結果を採用します。
主軸の計算
主軸の計算
指定された荷重条件で弾性応力解析を行う。
$P$:各節点へ作用する水平力のベクトル
$u_x(u_y)$:X(Y)方向加力時のX方向節点移動量のベクトル
$v_x(v_y)$:X(Y)方向加力時のY方向節点移動量のベクトル
と定義すると、水平力がX軸と角度Θで系に作用する場合、水平力がなす仕事Wは次式で表わされる。
$W$ = $\frac{1}{2}P^t(u_xcos^2Θ+(u_y+v_x)sinΘcosΘ+v_ysin^2Θ)$
$W$が極値を取る場合のΘを求める。
$W$ = $\frac{1}{2}P^t(u_x \frac{1+cos2Θ}{2}+(u_x+v_y) \frac{1}{2}sinΘ+v_y \frac{1-cos2Θ}{2}$
$ \frac{dW}{dΘ}$ = $\frac{1}{2}P^t((v_y-u_x)sin2Θ+(u_y+v_x)cos2Θ)$
$ \frac{dW}{dΘ}$ = 0 より
$tan2Θ$ = $- \frac{P^t(u_y+v_x)}{P^t(v_y-u_x)}$
施工時解析
施工時解析
指定により、長期応力解析を施工段階解析とすることが可能です。 施工時解析は以下のような解析を行います。
- 下層から順に1層ずつ部材を生成します。
- 1層部材を生成するごとに、上層の固定荷重を載荷します。
- 部材生成時には、これから生成される層の節点は初期座標に存在するものとして部材生成します。したがって、部材生成時には節点変位が0の状態から解析が開始し、下階の鉛直変位は累積されない変位となります。
- すべての部材生成および固定荷重を載荷した後、積載荷重を載荷します。
段階的耐力喪失解析
段階的耐力喪失解析
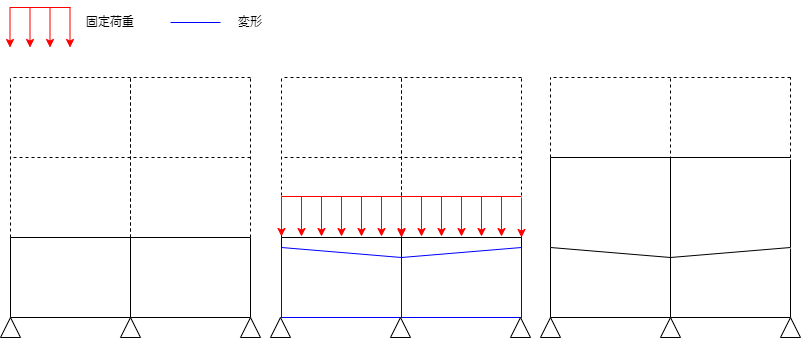
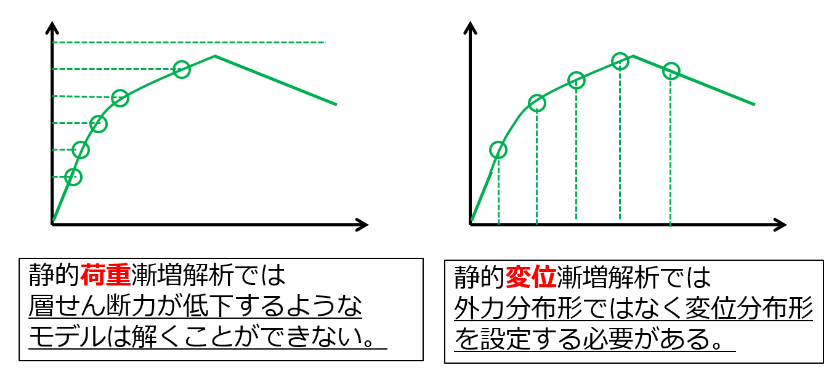
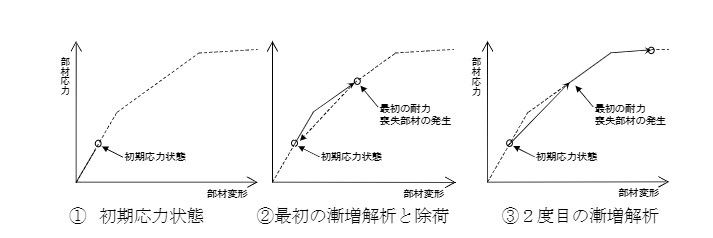
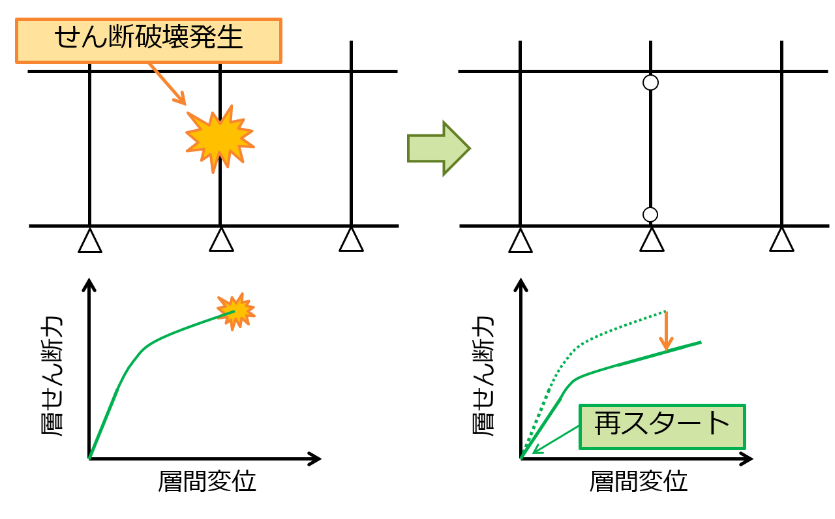
荷重漸増解析において、擬似的に耐力劣化を考慮する解析です。 通常の荷重漸増解析では、荷重が減少するような層として耐力劣化を生じる計算を行うことはできません。
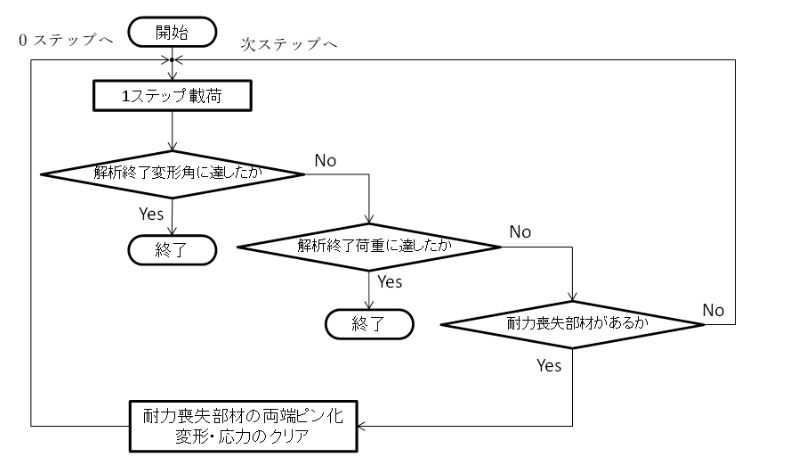
段階的耐力喪失解析では、以下のように擬似的に耐力劣化を考慮します。
- 耐力喪失変形角を設定します。
- せん断降伏後耐力喪失変形角に達する部材が発生するまで荷重漸増を行います。
- 耐力喪失変形角に達した部材が発生した場合、当該部材を両端ピンとしてせん断力を負担しない部材に変更したのち荷重を0から再載荷します。
- これを繰り返し、得られた荷重変形関係を包絡することで耐力劣化を考慮した曲線を得ます。
耐力喪失変形角直接指定の場合
耐力喪失開始変形角と終了変形角を指定します。
せん断降伏後、終了変形角を超えた部材が発生した際に、開始変形角を超える部材はまとめて両端ピンとして再載荷を行います。
FEMAによる非線形特性設定の場合
大梁
FEMAを用いた段階的耐力喪失解析を行う場合、以下のように計算されます。
各範囲内における塑性回転角は線形補間により算出します。
$b$: 梁幅
$D$: 梁せい
$\rho$ : 引張側鉄筋比
$\rho'$ : 圧縮側鉄筋比
$\rho_{bal}'$ : 釣り合い鉄筋比
$s$: せん断補強筋間隔
$V_s$: せん断耐力
$V$: 両端降伏時せん断力
$f_c'$: コンクリート強度(N/mm2)
“C”, “NC” は以下のように判定します。 “C” : $s <= D / 3 $ かつ $ Vs >= 0.75 * V $
塑性回転角は以下のように算出されます。 塑性回転角に達した梁は耐力喪失部材として除去されます。
| $\frac{\rho-\rho'}{\rho_{bal}} $ | $C/NC$ | $\frac{V}{bd\sqrt{f_c'}}$ | 塑性変形角 $a(rad)$ |
|---|---|---|---|
| ≦0.0 | C | ≦0.25 | 0.025 |
| ≦0.0 | C | ≧0.5 | 0.02 |
| ≧0.5 | C | ≦0.25 | 0.02 |
| ≧0.5 | C | ≧0.5 | 0.015 |
| ≦0.0 | NC | ≦0.25 | 0.02 |
| ≦0.0 | NC | ≧0.5 | 0.01 |
| ≧0.5 | NC | ≦0.25 | 0.01 |
| ≧0.5 | NC | ≧0.5 | 0.005 |
柱
柱については現状未対応となります。
04. 断面検定(許容応力度検定)
- 準拠する基準など
- 荷重の組合せ
- 採用応力
- 材料強度・許容応力度
- 鉄筋コンクリート造梁の断面検定
- 鉄筋コンクリート造柱の断面検定
- 鉄筋コンクリート造耐震壁の断面検定
- 鉄筋コンクリート造柱梁接合部の断面検定
- 鉄筋コンクリート造梁付着の断面検定
- 鉄筋コンクリート造水平接合面の検討
- 鉄骨造梁の断面検定
- 鉄骨造柱の断面検定
- 鉄骨造パネルゾーンの断面検定
- 冷間成形角型鋼管の断面検定
- CFT柱の断面検定
- 鉄骨鉄筋コンクリート造梁の断面検定
- 鉄骨鉄筋コンクリート造柱の断面検定
- 鉄骨鉄筋コンクリート造 耐震壁の断面検定
- 鉄骨鉄筋コンクリート造パネルゾーンの断面検定
- JFEシビル二重鋼管座屈補剛ブレースの断面検定
- 日鉄エンジニアリングアンボンドブレースの断面検定
- 鉄骨の断面検定における断面性能
- 鉄骨ブレースの断面検定
04. 断面検定(許容応力度検定)のサブセクション
準拠する基準など
準拠する基準等は以下の通りです。
- 建築基準法・同施行令・告示等
- 建築物の構造規定(日本建築センター編)(1997年版)
- 鉄筋コンクリート構造計算規準・同解説(1999年,2010年版)
- 鉄骨鉄筋コンクリート構造計算規準・同解説(1987年版)
- 鋼構造設計規準(1973年版)
- 建築耐震設計における保有耐力と変形性能(1990年版)
- 鋼構造塑性設計指針(1975年版)
荷重の組合せ
断面検討は、2007年版建築物の構造関係技術基準解説書(以下、構造規定と記します)により、以下の荷重組合せについて行います。
| 力の種類 | 想定する荷重状態 | 一般の場合 | 多雪区域 |
|---|---|---|---|
| 長期 | 常時 | G+P | G+P |
| 積雪時 | G+P+δ1・S | ||
| 短期 | 積雪時 | G+P+S | G+P+S |
| 暴風時 | G+P+W | G+P+W | |
| G+P+δ2・S+W | |||
| 地震時 | G+P+E | G+P+δ3・S+E |
$G$ :固定荷重によって生じる応力
$P$ :積載荷重によって生じる応力
$S$ :雪荷重によって生じる応力
$W$:風圧力によって生じる応力
$E$:地震力によって生じる応力
$δ1$:多雪区域における長期積雪荷重の低減係数で、直接入力することも可能です注1)。デフォルトは0.7とします。
$δ2,δ3$:多雪区域における暴風時および地震時の短期積雪荷重の低減係数で、直接入力できます注1)。デフォルトは0.35とします。
注1) メインメニュー「荷重・材料」→「積雪荷重」参照。
採用応力
■モーメント分布
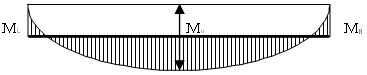
曲げモーメントの分布は2次曲線と仮定して以下の式で計算します。
$M = M_1+ \frac{(-M_1-M_2+4M_0) \cdot x}{L}- \frac{4M_0x^2}{L^2}$$M_{1},M_{2}$ :端部モーメント
$M_{0}$ :単純梁の中央モーメント
$x$ :応力採用位置
$L$ :材長
■一本部材指定時の採用応力
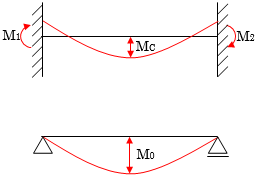
大梁において一本部材指定を行った場合のM0は、端部のせん断力と釣り合う荷重が等分布として単純梁に作用したものと仮定した場合のA式もしくは,一本部材とした場合の中央位置におけるモーメントを中央に位置する分割部材の端部モーメントおよびM0から算出した場合のB式のうち、大きい数値を採用します。
A. $ M_0 = \frac{(Q_1+Q_2) \cdot L}{8} $
$Q_1,Q_2$ :端部せん断力
$L$ :材長
B. $ M_c = M_{c1}+\frac{(-M_{c1}-M_{c2}+4M_{c0}) \cdot x}{L} -\frac{4M_{c0} \cdot x^2}{L^2}$
$M_1,M_2$ :一本部材の端部モーメント
$M_0$ :一本部材の単純梁中央モーメント
$M_{c1},M_{c2}$ :中央部分割部材の端部モーメント
$M_{c0}$ :中央部分割部材の単純梁中央モーメント
$x$ :中央部分割部材の応力採用位置
$L$ :中央部分割部材の材長
$M_c$ :一本部材の中央モーメント
■大梁直交方向加力時採用応力
大梁の採用応力は、各水平荷重加力ケースにおいて最大せん断力が発生するケースを採用応力とします。したがって、加力方向を0°方向・90°方向としていない場合もしくは大梁がX軸、Y軸に平行でない場合には、大梁の方向と異なる加力ケースの応力が採用される場合があります。その場合、計算書出力の断面検定表においてその旨が出力されます。
材料強度・許容応力度
コンクリート
コンクリートの使用材料は、各階で柱・壁、梁・床ごとに指定できます。コンクリートの材料定数および許容応力度は2010年版RC規準によります。
| 種類 | 長期 | 短期 | ||||
|---|---|---|---|---|---|---|
| 圧縮 | 引張 | せん断 | 圧縮 | 引張 | せん断 | |
| 普通コンクリート | 1/3・Fc | - | 1/30・Fcかつ (0.49+1/100・Fc)以下 | 長期に対する 値の2倍 | - | 長期に対する値の1.5倍 |
| 軽量コンクリート 1種・2種 | 普通コンクリートに 対する値の0.9倍 | |||||
コンクリートの付着許容応力度 (N/mm2)
| 種類 | 長期 | 短期 | |
|---|---|---|---|
| 上端筋 | その他の鉄筋 | - | |
| 異形鉄筋 | 1/15・Fcかつ (0.9+2/75・Fc)以下 | 1/10・Fcかつ (1.35+1/25・Fc)以下 | 長期に対する値の1.5倍 |
| 丸鋼 | 4/100・Fcかつ 0.9以下 | 6/100・Fcかつ 1.35以下 | |
RC規準1999付着検討時のコンクリートの付着許容応力度 (N/mm2)
| 種類 | 長期 | 短期 | |
|---|---|---|---|
| 上端筋 | その他の鉄筋 | - | |
| 異形鉄筋 | 0.8×(1/60・Fc+0.6) | 1/60・Fc+0.6 | 長期に対する値の1.5倍 |
| 丸鋼 | |||
・コンクリートの引張応力は無視します。
・コンクリートのヤング係数(Ec)、せん断弾性係数(G)は下式によります。
$$E_c = 3.35 \cdot10^4 \cdot \left( \frac{\gamma}{24} \right) ^2 \cdot \left( \frac{F_c}{60} \right) ^\frac{1}{3}$$ $$G = \frac{E_c}{2(1+v)}$$$E_c$:コンクリートの設計基準強度(N/mm2)
$G$:コンクリートのせん断弾性係数(N/mm2)
$γ$:コンクリートの気乾単位体積重量で、鉄筋コンクリートの単位体積重量の数値から1.0を減じた値とする(kN/m3)
$ν$:ポアソン比(=0.2)
・断面算定においてコンクリートに対する鉄筋のヤング係数比(n)は下表の値とします。なお、非線形解析に用いるnについては各材料の実際のヤング係数から計算されます。
| Fc(N/mm2) | ヤング係数比n |
|---|---|
| Fc≦27 | 15 |
| 27<Fc≦36 | 13 |
| 36<Fc≦48 | 11 |
| 48<Fc≦60 | 9 |
| 60<Fc≦120 | 7 |
鉄筋
鉄筋の使用材料は階と部位による指定、または鉄筋径ごとの指定が可能です。各指定の優先順位は、鉄筋径ごとの指定が優先となります。したがって、鉄筋径の範囲に定義されていない径についてのみ階と部位による指定が適用されます。
鉄筋の許容応力度は構造規定によります。高強度せん断補強筋の許容応力度については、メーカーの公称値とします。
鉄筋の許容応力度 (N/mm2)
| 長期 | 短期 | |||
|---|---|---|---|---|
| 引張・圧縮 | せん断 | 引張・圧縮 | せん断 | |
| SR235 | 155 | 155 | 235 | 235 |
| SR295 | 155 | 195 | 295 | 295 |
| SD295A,B | 195 | 195 | 295 | 295 |
| SD345 | 215(195*1) | 195 | 345 | 345 |
| SD390 | 215(195*1) | 195 | 390 | 390 |
| SD490 | 215(195*1) | 195 | 490 | 390(キョウエイリングは適用範囲内であれば490) |
| USD685 | 215 | 195 | 685 | 590 |
*1:D29以上の太さの鉄筋に対しては( )内の数値とします。
高強度せん断補強筋の許容せん断応力度 (N/mm2)
| 製品 | 長期 | 短期 | 終局 |
|---|---|---|---|
| ウルボン1275【SBPD1275/1420】 | 195 | 585 | 1275(785*1) |
| ウルボン785【UB785】 | 195 | 590 | 785 |
| リバーボン785【KW785】 | 195 | 590 | 785 |
| スミフープ,ストロングフープ,デーフープ【KSS785】 | 195 | 590 | 785 |
| UHYフープ【SHD685】 | 195 | 590 | 685 |
| エヌエスハイデック685H【HDC685】 | 195 | 590 | 685 |
| スーパーフープ【KH785】 | 195 | 590 | 785 |
*1:()内は柱のせん断補強筋として単独で外周フープに135°フック閉鎖形を使用する場合の数値です。
高強度せん断補強筋の呼び名の公称直径、最外径、公称断面積、公称周長の対応一覧
| 製品名 | 呼び名 | 公称直径(mm) | 最外径(mm) | 公称断面積(cm2) | 公称周長(cm) |
|---|---|---|---|---|---|
| スミフープ、ストロングフープ、デーフープ【KSS785】 エヌエスハイデック685H【HDC685】 UHYフープ【SHD685】 | 6 | 6 | 6 | 0.3167 | 2.000 |
| 8 | 8 | 8 | 0.4951 | 2.500 | |
| 10 | 9.53 | 9.53 | 0.7133 | 3.000 | |
| 13 | 12.7 | 12.7 | 1.267 | 4.000 | |
| 16 | 15.9 | 15.9 | 1.986 | 5.000 | |
| ウルボン1275【SBPD】 ウルボン785【UB785】 | 7 | 7.1 | 7.3 | 0.4 | - |
| 9 | 9.0 | 9.15 | 0.64 | - | |
| 10 | 10.7 | 11.10 | 0.90 | - | |
| 11 | 10.7 | 11.10 | 0.90 | - | |
| 12 | 12.6 | 13.10 | 1.25 | - | |
| 13 | 12.6 | 13.10 | 1.25 | - | |
| 15 | 14.7 | 14.7 | 1.697 | - | |
| 16 | 16.5 | 16.5 | 1.697 | - | |
| 17 | 16.5 | 16.5 | 2.138 | - | |
| リバーボン1275【SBPDN】 リバーボン785【KW785】 | 7 | 7.1 | 7.1 | 0.40 | 2.28 |
| 9 | 9.0 | 9.0 | 0.64 | 2.87 | |
| 10 | 10.7 | 10.7 | 0.90 | 3.49 | |
| 12 | 12.6 | 12.6 | 1.25 | 4.12 | |
| 13 | 12.6 | 12.6 | 1.25 | 4.12 | |
| 16 | 15.9 | 15.9 | 1.986 | 5.0 | |
| スーパーフープ【KH785】 | 10 | 9.53 | 9.53 | 0.7133 | 3.000 |
| 13 | 12.7 | 12.7 | 1.267 | 4.000 | |
| 16 | 15.9 | 15.9 | 1.986 | 5.000 | |
| パワーリング785【SPR785】 | 10 | 9.53 | 9.53 | 0.7133 | 3.000 |
| 13 | 12.7 | 12.7 | 1.267 | 4.000 | |
| 16 | 15.9 | 15.9 | 1.986 | 5.000 |
鉄骨
鉄骨の使用材料は、階と部位により設定します。柱・梁については、フランジ・ウェブごとの指定が可能です。また、梁については左端・中央・右端、柱については柱頭・柱脚に分けて設定できます。なお、鋼材の許容応力度は構造規定に基づきます。
鋼材の許容応力度 (N/mm2)
| 種別 | 長期 | 短期 | ||||||
|---|---|---|---|---|---|---|---|---|
| 圧縮 | 引張 | 曲げ | せん断 | 圧縮 | 引張 | 曲げ | せん断 | |
| 一般構造用圧延鋼材 | $ \frac{F}{1.5} $ | $ \frac{F}{1.5 \sqrt 3} $ | 長期に対する値の1.5倍 | |||||
| 溶接構造用圧延鋼材 | ||||||||
| 建築構造用圧延鋼材 | ||||||||
鋼材の基準強度 (N/mm2)
| 一般構造用 | 溶接構造用 | |||||
|---|---|---|---|---|---|---|
| SS400 | SS490 | SM400 | SM490 | SM520 | ||
| F | 厚さ40mm以下 | 235 | 275 | 235 | 325 | 355 |
| 厚さ40mmを超え100mm以下 | 215 | 255 | 215 | 295 | 335*1 | |
| 厚さ75mmを超え100mm以下 | ― | ― | ― | ― | 325 | |
*1:SM520については、厚さ40mmを超え75mm以下のF値を示します。
| 建築構造用 | 建築構造用高性能590[N/mm2] | |||
|---|---|---|---|---|
| SN400 | SN490 | SA440 | ||
| F | 厚さ40mm以下 | 235 | 325 | 440 |
| 厚さ40mmを超え100mm以下 | 215 | 295 | - | |
| 一般構造用角形鋼 | 冷間成形角形鋼管 | |||||
|---|---|---|---|---|---|---|
| STKR400 | STKR490 | BCR295 | BCP235 | BCP325 | ||
| F | 厚さ40mm以下 | 235 | 325 | 295 | 235 | 325 |
| 厚さ40mmを超え100mm以下 | 215 | 295 | - | - | - | |
注)冷間成形角形鋼管を使用する場合、「冷間成形角形鋼管設計・施工マニュアル」(財団法人日本建築センター)に基づく計算は行っておりませんので予めご了承ください。
圧縮材の座屈の許容応力度
圧縮材の座屈の長期許容応力度(fcL)は次式で算定します。なお、圧縮材の座屈の短期許容応力度(fcS)は長期許容応力度(fcL)の1.5倍とします。
$$ f_{cL} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \frac{F}{v} \left( 1-0.4 \cdot \left( \frac{\lambda}{\Lambda} \right) ^2 \right) & \displaystyle \left( \lambda \leq \Lambda \right) \\ \displaystyle \frac{ \frac{18}{65} \cdot F}{ \left( \frac{\lambda}{\Lambda} \right) ^2 }& \displaystyle \left( \Lambda < \lambda \right) \end{array} \right. \end{align} $$$f_{cL}$:圧縮材の座屈の長期許容応力度
$F$:鋼材の規準強度(N/mm2)
$λ$:有効細長比(= $l_k$/i)
$i$:座屈軸についての断面2次半径(mm)
$l_k$:有効座屈長さ(mm)
$Λ$:限界細長比
$ν$:安全率
${\Lambda} = \frac{1500}{ \sqrt{ \frac{F}{1.5}} }$ $v = \frac{3}{2}+\frac{2}{3} \left( \frac{\lambda}{\Lambda} \right) ^2 $曲げ材の座屈の許容応力度
曲げ材の座屈の長期許容応力度( $f_{bL}$)は下式で求めます。なお、曲げ材の座屈の短期許容応力度( $f_{bS}$)は長期許容応力度( $f_{bL}$)の1.5倍とします。
$$f_{bL} = \max (f_{b1}, \quad f_{b2})$$ $$ \begin{eqnarray} f_{b1} &=& F \cdot \left( \frac{2}{3}- \frac{4}{15} \cdot \frac{\left( \frac{l_b}{i} \right) ^2}{C \cdot \Lambda^2} \right) \\ f_{b2} &=& \frac{89000}{ \left( \frac{l_b \cdot h}{A_f} \right)} \end{eqnarray} $$$f_{bL}$:曲げ材の座屈の長期許容応力度
$l_b$:圧縮フランジの支点間距離(mm)
$i$:圧縮フランジと曲げ材のせいの6分の1とからなるT形断面のウェブ軸周りの断面2次半径(mm)
$h$:曲げ材のせい(mm)
$Λ$:限界細長比
$A_{f}$:圧縮フランジの断面積(mm2)
$C $:修正係数
$C = 1.75+1.05 \cdot \left( \frac{M_2}{M_1} \right)+0.3 \cdot \left( \frac{M_2}{M_1} \right)^2$$M_{1}$、 $M_{2}$については、座屈区間端部における強軸まわりの曲げモーメントの大きい方を $M_1$、小さいほうを $M_2$とします。 $M_2$/ $M_1$においては、当該曲げモーメントが複曲率となる場合は正、単曲率となる場合は負とします。また、座屈区間端部より中央部の曲げモーメントが大きい場合はC=1.0とします。
鉄筋コンクリート造梁の断面検定
記号説明
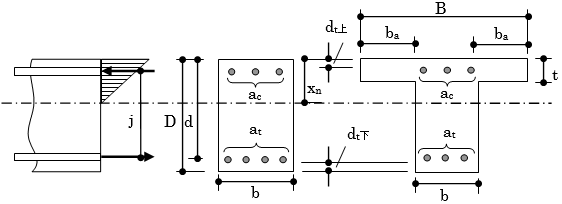
$B$ :T形断面部材の有効幅(mm)
$b$ :長方形梁の幅(mm)
$D$ :梁せい(mm)
$d_t$ :引張縁から引張鉄筋重心までの距離(mm)
$d$ :圧縮縁から引張鉄筋重心までの距離(有効せい)(=D-dt)(mm)
$j$ :梁の応力中心間距離(=7/8・d)(mm)
$a_t$ :引張鉄筋の断面積(mm2)
$a_c$ :圧縮鉄筋の断面積(mm2)
$p_w$ :せん断補強筋比(%)
$α_L$ :長期のせん断スパン比M/(Qd)による割増係数
$α_{S1}$ :短期正加力時のせん断スパン比M/( $Q_d$)による割増係数
$α_{S2}$ :短期負加力時のせん断スパン比M/( $Q_d$)による割増係数
$l$ :梁の内法スパン長さ(mm)
$t$ :スラブ厚(mm)
[梁の曲げに対する断面算定]
$M_L$ :長期曲げモーメント
$M_{sn}$ :積雪荷重曲げモーメント
$M_{E1}$ :正加力時の地震荷重による曲げモーメント
$M_{E2}$ :負加力時の地震荷重による曲げモーメント
$M_{w1}$ :正加力時の風圧力による曲げモーメント
$M_{w2}$ :負加力時の風圧力による曲げモーメント
$M_S$ :短期設計用曲げモーメント注1)
$M_{AL}$ :長期許容曲げモーメント
$M_{AS}$ :短期許容曲げモーメント
$M_y$ :終局曲げ強度
$M_L/M_{AL}$ :長期曲げモーメントに対する検定値
$M_S/M_{AS}$ :短期曲げモーメントに対する検定値
[梁のせん断に対する断面算定]
$Q_L$ :長期せん断力
$Q_{sn}$ :積雪荷重によるせん断力
$Q_E$ :地震荷重によるせん断力
$Q_w$ :風圧力によるせん断力
$Q_D$ :短期設計用せん断力
$Q_{AL}$ :長期許容せん断力
$Q_{AS}$ :短期許容せん断力
$Q_L/Q_{AL}$ :長期せん断力に対する検定値
$Q_D/Q_{AS}$ :短期せん断力に対する検定値
曲げモーメントに対する検討
梁の長期および短期の許容曲げモーメントが設計用曲げモーメント以上であることを以下の検定式により確認します。
$ M_L/M_{AL} \verb|≦|1.0 $ 長期曲げモーメントに対する検定
$ M_S/M_{AS} \verb|≦|1.0 $ 短期曲げモーメントに対する検定
スラブ付き梁であるT形梁の有効幅(B)は、長方形梁の幅(b)に両側または片側の協力幅( $b_a$)を加えたものとします。協力幅(ba)の算定については、“断面性能の計算式"を参照してください
a) 梁の許容曲げモーメント( $M_A$)
長方形梁の許容曲げモーメント( $M_A$)は、RC規準13条により次式で算定します。また、T形梁で上端引張になる場合においても、スラブを無視した長方形梁として次式で算定します。
$$M_A = C \cdot b \cdot d^2$$$M_A$:許容曲げモーメント
Cは以下に求める $C_1,C_2$のうち小さいほうの数値とします。
$C_1 = \frac{p_t \cdot f_c}{3 \cdot x_n} (n \cdot (1-x_{n1})(3-x_{n1})-\gamma \cdot (n-1)(x_{n1}-d_{c1})(3 \cdot d_{c1}-x_{n1}) )$ $C_2 = \frac{p_t \cdot f_c}{3 \cdot n \cdot (1-x_{n1}} (n \cdot (1-x_{n1})(3-x_{n1})-\gamma \cdot (n-1)(x_{n1}-d_{c1})(3 \cdot d_{c1}-x_{n1}) )$$d_c$:圧縮縁から圧縮鉄筋重心までの距離(=dt)(mm)
$d_{c1}$=dc/d
$f_c$:コンクリートの設計基準強度(N/mm2)
$n$:ヤング係数比
$γ$:複筋比(=ac/at)
$p_t$:引張鉄筋比(=at/(b・d))
$x_n$:圧縮縁より中立軸までの距離(mm)
$x_{n1} = p_t \cdot \left[ \sqrt({ n \cdot (1+\gamma)-\gamma )^2+ \frac{2}{p_t} ( n \cdot (1+\gamma \cdot d_{c1})-\gamma \cdot d_{c1} ) } - ( n \cdot (1+\gamma)-\gamma ) \right]$$p_{tb}$:釣合鉄筋比
$P_{tb} = \frac{1}{ 2 \cdot \left( 1+ \frac{f_t}{n \cdot f_c} \right) \cdot \left[ \frac{f_t}{n \cdot f_c} ( n+(n-1) \cdot \gamma \cdot d_{c1}-(n-1) \cdot \gamma \cdot(1-d_{c1}) \right]}$引張鉄筋比( $p_t$)が釣合鉄筋比( $p_{tb}$)以下の場合は、許容曲げモーメント( $M_A$)を次式により算定します。T形梁で下端引張になる場合においても、一般に有効幅(B)が大きいためにほとんどが釣合鉄筋比以下となることから、次式により算定します。また、釣合鉄筋比が負の場合においても次式により算定します。
$$M_A = \alpha_t \cdot f_t \cdot j$$$f_t$:引張鉄筋の許容引張応力度(N/mm2)
b) 梁主筋の2段筋重心位置
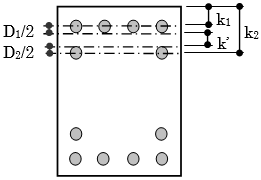
梁主筋の2段筋重心位置は、ユーザーによる入力がない場合、鉄筋コンクリート造配筋指針・同解説(以下、RC配筋指針と記します)により次式で算定します。
$$k_2 = k_1+ \frac{D_1}{2}+k'+ \frac{D_2}{2}$$$k_1$:1段筋重心位置(mm)
$k_2$:2段筋重心位置(mm)
$D_1$:1段筋最外径(mm)
$D_2$:2段筋最外径(mm)
$k'$:鉄筋のあき(mm)
$k' = \max (25, \quad 1.5 \cdot d')$ $d' = (d_1+d_2)/2$$d_1$:1段筋径(呼び名の数値)
$d_2$:2段筋径(呼び名の数値)
■ 重心位置の入力について
1段筋重心位置( $k_1$)は、①と②の2通りの入力方法があります。両方を入力した場合は、②による入力値が優先されます。
2段筋重心位置( $k_2$)は②による個別入力のみに対応しています。未入力の場合は内部計算値を採用します。
①メインメニュー「使用材料」→「鉄筋」→「鉄筋重心位置」で、方向および階ごとに一括で入力できます。デフォルト値は75mmです。
②メインメニュー「RC大梁リスト」→「詳細」で、符号ごとに個別に入力できます。
c) 異種強度梁の場合
異種強度梁の曲げに対する許容応力度検定は、圧縮側のコンクリート強度(上端引張の場合
$F_{cd}$, 下端引張の場合
$F_{cu}$)を用いて既存の方法で行います。
なお、T形梁による耐力計算を選択した場合、長方形梁とT形梁で耐力が大きくなる方を採用します。
せん断力に対する検討
梁の長期および短期の許容せん断力が設計用せん断力以上であることを、以下の検定式により確認します。
$ Q_L/Q_{AL} \verb|≦| 1.0 $ 長期せん断力に対する検定
$ Q_D/Q_{AS} \verb|≦| 1.0 $ 短期せん断力に対する検定
a) 梁の許容せん断力( $Q_A$)
■ 長期許容せん断力( $Q_{AL}$)
梁の長期許容せん断力( $Q_{AL}$)は、長期荷重によるせん断ひび割れの発生を前提とした下式により算定します。
$$Q_{AL} = b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_s(p_w-0.002) )$$ $α = \frac{4}{\frac{M}{Q \cdot d}+1}$かつ
$1.0 \verb|≦| \alpha \verb|≦| 2.0$とする。
$Q_{AL}$:長期許容せん断力
$f_s$:コンクリートの長期許容せん断応力度(N/mm2)
$_{w}f _{t}$:せん断補強筋の長期許容引張応力度(N/mm2)
$p_w$:せん断補強筋比(= $a_w/(b・x)$)
$p_w$の値が0.6%を超える場合は0.6%とする。
$a_w$:1組のせん断補強筋の断面積(mm2)
x:せん断補強筋の間隔(mm)
■ 短期許容せん断力( $Q_{AS}$)
梁の短期許容せん断力( $Q_{AS}$)は下式により算定します。
$$ Q_{AS} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle b \cdot j (\frac{2}{3} \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_s(p_w-0.002) ) & \displaystyle \left( \text{損傷制御のための検討} \right) \\ \displaystyle b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_s(p_w-0.002) ) & \displaystyle \left( \text{安全確保のための検討} \right) \end{array} \right. \end{align} $$ $\alpha = \frac{4}{\frac{M}{Q \cdot d}+1}$かつ
$1.0 \verb|≦| \alpha \verb|≦| 2.0$とする。
$Q_{AS}$:短期許容せん断力
$f_s$:コンクリートの短期許容せん断応力度(N/mm2)
$_wf _s $:せん断補強筋の短期許容引張応力度(N/mm2)
$p_w$:せん断補強筋比(= $a_w/(b・x)$)
1.2%を超える場合は1.2%とする。
・ $α$の算定に用いるせん断スパン比( $M/Q_d$)は、各検定位置のうちモーメントが最大となる位置の値を採用します。このとき、せん断力( $Q$)に水平荷重時割増係数( $n$)は考慮しません。
b) 梁の設計用せん断力( $Q_D$)
梁の短期設計用せん断力( $Q_D$)は、ユーザー選択注2)により $Q_{D1}$と$Q_{D2}$のいずれか、または小さいほうとします。
$$Q_D = \min (Q_{D1}, Q_{D2})$$ $$ Q_{D1} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle Q_0+ \frac{\sum {_B}M_y}{l} & \displaystyle \left( \text{MK785の場合} \right) \\ \displaystyle Q_L+ \frac{\sum {_B}M_y}{l} & \displaystyle \left( \text{上記以外の鉄筋の場合} \right) \end{array} \right. \end{align} $$ $$Q_{D2} = Q_L+ n \cdot Q_E$$$Q_D$:短期設計用せん断力
$Q_L$:長期設計用せん断力
$Q_0$:単純梁の長期せん断力
$Q_E$:地震荷重によるせん断力
$n$:水平荷重時せん断力の割増係数
$Σ_BM _y $:梁両端の降伏曲げモーメントの絶対値の和(= $ΣM_u $)
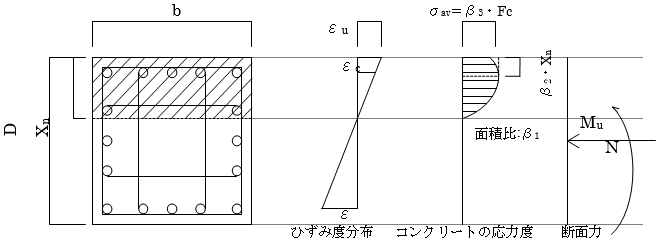
梁の曲げ終局強度( $M_u$)は5.1.1(2)を参照してください。このとき、 $M_u$にスラブ筋は考慮しません。
※積雪時、暴風時の短期設計用せん断力は以下とします。
・積雪時: $Q_D=Q_L+Q_{sn}$
・暴風時: $Q_D=Q_L+Q_w$
c) 高強度せん断補強筋を使用する場合について
■せん断補強筋比( $p_w$)
高強度せん断補強筋を使用する場合は、許容せん断力( $Q_A$)算定時に用いるせん断補強筋比( $p_w$)の制限値を以下とします。
| 製品名 | 長期pw | 短期pw |
|---|---|---|
| ウルボン1275【SBPD1275】BCJ評定-RC0220-05 MSRB-9009 | 0.6% | 1.2%(損傷制御) 1.0%(安全性確保) |
| リバーボン1275【SBPDN1275/1420】 | 0.6% | 0.8% |
| ウルボン785【UB785】 | 0.6% | 1.2%(損傷制御) 1.0%(安全性確保) |
| リバーボン785【KW785】 | 0.6% | 0.8% |
| スミフープ,ストロングフープ,デーフープ【KSS785】 | 0.6% | 0.8% |
| UHYフープ【SHD685】 | 0.6% | 1.2% |
| エヌエスハイデック685H【HDC685】 | 0.6% | 0.8% |
| スーパーフープ【KH785】 GBRC評定 第10-10号改 平成23年9月27日 MSRB-0061 | 0.6% | 1.2% もしくは 1.0%×(Fc/27)の小さい方 |
| スーパーフープ【KH685】 SABTEC評価 15-02 MSRB-0087 | 0.6% | 1.2% もしくは 1.2%×(Fc/27)の小さい方 |
| パワーリング785【SPR785】 BCJ評定-RC0395-02 MSRB-0066 | 0.6% | 1.2%(損傷制御) 1.0%(安全性確保) |
| パワーリング685【SPR685】 SABTEC評価15-03 MSRB-0094 | 0.6% | 1.2% もしくは 1.2%×(Fc/27)の小さい方 |
| エムケーフープ785【MK785】 BCJ評定-RC0419-03 MSRB-0067 | 0.6% | 1.2% |
■許容せん断力( $Q_A$)
高強度せん断補強筋を使用する場合の許容せん断力( $Q_A$)は下式で算定します。
【ウルボン1275の場合】
$$Q_{AS} = \phi \cdot b \cdot D \cdot \left( 850 \cdot \sqrt{\frac{W_0}{D} \cdot \frac{p_W}{_L\sigma_0+3} }\cdot \frac{M}{Q \cdot D}+1 \right) \cdot _L\tau_{SC}$$ $W_0 = \frac{W_a}{3 \cdot Q_L/(Q_L+Q_E)+1}$$_L\tau_{SC}$ = $\sqrt{\sigma_T{^2}+\sigma_T \cdot {_L\sigma}_0}/\kappa$
(損傷制御のための検討)
・ $M/(Q・D)$が2.0を超える場合は2.0とします。
・ $_Lσ_0$が0以下の場合、 $_Lτ _{SC} $の算定では負として扱い、 $ Q _{AS} $算定では0として扱います。
・ $_Lσ_0$が18N/mm2を超える場合、 $_Lσ_0$が18N/mm2とします。
また、損傷制御のための検討を選択していた場合でも、基礎梁および軽量コンクリートは対象外のため、安全性確保として検討します。
(安全性確保のための検討)
$Q_{AS} = b \cdot j( \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001))$$f_s$は軽量コンクリートの場合、0.75倍とします。
【スーパーフープKH785,KH685の場合】
$Q_{AL} = b \cdot j ( \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.002))$$Q_{AS} = b \cdot j (\beta_c \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.002))$ (損傷制御のための検討)
$Q_{AS} = b \cdot j ( \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.002))$ (安全確保のための検討)
$β_c:1-(100pw-0.2)/3$$Q_{AL}$:長期許容せん断力
$Q_{AS}$:短期許容せん断力
【パワーリング785の場合】
SPR785の損傷制御のための検討、安全性確保のための検討は下式で算定します。
$Q_{AS} = b \cdot j (2/3 \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (損傷制御のための検討)
$Q_{AS} = b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (安全確保のための検討)
また、損傷制御のための検討を選択していた場合でも、梁せいが1000mmを超える梁部材、基礎梁については安全性確保のための検討で算定します。
【パワーリング685の場合】
SPR685の損傷制御のための検討、安全性確保のための検討は下式で算定します。
$Q_{AS} = b \cdot j (\beta_c \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001))$ (損傷制御のための検討)
$ Q_{AS} = b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) ) $ (安全確保のための検討)
$β_c$は以下の式を用いるか、2/3とするか選択できます。ただし、梁内法スパン長比が3.0未満の場合、$β_c$=2/3とします。
$\beta_c = 1-(100p_w-0.2)/3$【エムケーフープの場合】
MK785の損傷制御のための検討、安全性確保のための検討は下式で算定します。
$Q_{AS} = b \cdot j (2/3 \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (損傷制御のための検討)
$Q_{AS} = b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (安全確保のための検討)
また、損傷制御のための検討を選択していた場合でも、梁せいが1000mmを超える梁部材については安全性確保のための検討で算定します。
【上記以外の高強度せん断補強筋の場合】
$Q_{AS} = b \cdot j (2/3 \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (損傷制御のための検討)
$Q_{AS} = b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (安全確保のための検討)
※上式は暫定対応による計算となっています。メーカーの設計指針と計算内容が異なる場合があります。
注2) メインメニュー「設計・計算条件」→「断面算定条件」→「RC造」参照。
d) 異種強度梁の場合
異種強度梁のせん断に対する許容応力度検定は、等価平均強度
$F_{ce}$による許容せん断応力度を用います。
等価平均強度は以下のように計算されます。
ただし、等価平均強度は梁下部のコンクリート強度を上限とします。
$A_u$ : 梁上部の断面積(スラブの協力幅含む) $A_d$ : 梁下部の断面積 $F_{cu}$ : 梁上部のFc $F_{cd}$ : 梁下部のFc
鉄筋コンクリート造柱の断面検定
記号説明
$b$ :柱幅(mm)
$D$ :柱せい(mm)
$d_t$ :引張縁から引張鉄筋重心までの距離(mm)
$d$ :圧縮縁から引張鉄筋重心までの距離(有効せい)(= $D-d_t$)(mm)
$j$ :柱の応力中心間距離(=7/8・d)(mm)
$a_t$ :引張鉄筋の断面積(mm2)
$a_c$ :圧縮鉄筋の断面積(mm2)
$p_w$ :せん断補強筋比(%)
$p_g$ :主筋全断面積のコンクリート全断面積に対する比
$α$ :せん断スパン比 $M/(Q_d)$による割増係数
[柱の軸方向と曲げに対する断面算定]
$N_L$ :長期軸力
$N_{sn}$ :積雪荷重による軸力
$N_{E1}$ :正加加力時の地震荷重による軸力
$N_{E2}$ :負加加力時の地震荷重による軸力
$N_{w1}$ :正加加力時の風圧力による軸力
$N_{w2}$ :負加加力時の風圧力による軸力
$N_{S1}$ :短期設計用軸力(柱脚モーメント負側最大時)
$N_{S2}$ :短期設計用軸力(柱脚モーメント正側最大時)
$M_L$ :長期曲げモーメント
$M_{sn}$ :積雪荷重曲げモーメント
$M_{E1}$ :正加力時の地震荷重による曲げモーメント
$M_{E2}$ :負加力時の地震荷重による曲げモーメント
$M_{w1}$ :正加力時の風圧力による曲げモーメント
$M_{w2}$ :負加力時の風圧力による曲げモーメント
$M_{S1}$ :短期設計用曲げモーメント(負側)注1)
$M_{S2}$ :短期設計用曲げモーメント(正側)注1)
$_cM_y$ :柱の終局曲げモーメント
$M_{AL}$ :長期許容曲げモーメント
$M_{AS1}$ :短期許容曲げモーメント(負側)
$M_{AS2}$ :短期許容曲げモーメント(正側)
$M_L/M_{AL}$ :長期曲げモーメントに対する検定値
$M_{S1}/M_{AS1}$ :短期曲げモーメントに対する検定値
$M_{S2}/M_{AS2}$ :短期曲げモーメントに対する検定値
[柱のせん断に対する断面算定]
$Q_L$ :長期せん断力
$Q_{sn}$ :積雪荷重によるせん断力
$Q_E$ :地震荷重によるせん断力
$Q_w$ :風圧力によるせん断力
$Q_D$ :短期設計用せん断力
$Q_{AL}$ :長期許容せん断力
$Q_{AS}$ :短期許容せん断力
注1) 長期は節点位置、水平荷重時はフェイス位置の応力を採用します。
軸方向力と曲げに対する検討
柱の長期および短期許容軸力(モーメント0を仮定した場合)は以下で計算されます。
$$N_A = min( f_c・A_e, _rf_c・A_e / n )$$$A_e$ : 等価断面積(= $A+(n-1)・A_s$)
$A $ : 柱の断面積
$E_s$ : 鉄筋のヤング係数
$E_c$ : コンクリートのヤング係数
$f_c$ : コンクリート許容応力度
$_rf_c$ : 鉄筋許容応力度
$n$ : ヤング係数比 (RC基準による)
柱の長期および短期の許容曲げモーメントが設計用曲げモーメント以上であることを以下の検定式により確認します。
$M_L/M_{AL} \verb|≦| 1.0$ 長期曲げモーメントに対する検定
$M_S/M_{AS} \verb|≦| 1.0$ 短期曲げモーメントに対する検定
指定により2軸曲げを考慮した場合以下のように計算します。
・矩形断面の場合
$M_{SX}/M_{ASX}+M_{SY}/M_{ASY} \verb|≦| 1.0$・円形断面の場合
$(M_{SX}/M_{ASX})^2+(M_{SY}/M_{ASY})^2 \verb|≦| 1.0$許容曲げモーメント( $M_A$)
RC規準14条により、軸力( $N$)と曲げモーメントを同時に受ける柱において、軸力( $N$)を受ける状態で以下の1~3に対して求めたそれぞれの曲げモーメントのうち最小値を許容曲げモーメント( $M_A$)とします。
圧縮縁がコンクリートの許容圧縮応力度( $f_c$)に達したとき
圧縮側鉄筋が鉄筋の許容圧縮応力度( $_rf_c$)に達したとき
引張側鉄筋が鉄筋の許容引張応力度( $f_t$)に達したとき
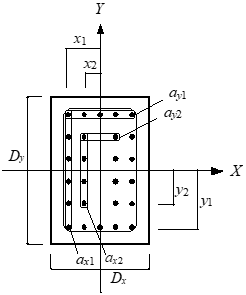
・寄筋が存在する場合、寄筋も許容曲げモーメント算定に考慮されます。寄筋の位置は、隅角部の鉄筋とのあきを25mmもしくは主筋最外径の1.5倍の大きい方の間隔として計算します。
・直交鉄筋は断面中央に集約して考慮されます。
せん断力に対する検討
柱の長期および短期の許容せん断力が設計用せん断力以上であることを、以下により確認します。
$Q_{AL} \verb|≧| Q_L$ 長期せん断力に対する検定
$Q_{AS} \verb|≧| Q_D$ 短期せん断力に対する検定
a) 柱の許容せん断力( $Q_A$)
■長期許容せん断力( $Q_{AL}$)
柱の長期許容せん断力( $Q_{AL}$)は下式により算定します。
$$Q_{AL} =b \cdot j \cdot \alpha \cdot f_s$$ $\alpha = \frac{4}{\frac{M}{Q \cdot d}+1}$かつ
$1.0 \verb|≦| \alpha \verb|≦| 1.5$とする。
$Q_{AL}$:長期許容せん断力(N)
$f_s$:コンクリートの長期許容せん断応力度(N/mm2)
■短期許容せん断力( $Q_{As}$)
柱の短期許容せん断力( $Q_{AS}$)は下式により算定します。
$$ Q_{AS} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle b \cdot j \left( \frac{2}{3} \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.002) \right) & \displaystyle \left( \text{損傷制御のための検討} \right) \\ \displaystyle b \cdot j ( f_s+0.5 \cdot {_w}f_t(p_w-0.002) ) & \displaystyle \left( \text{安全確保のための検討} \right) \end{array} \right. \end{align} $$ $\alpha = \frac{4}{\frac{M}{Q \cdot d}+1}$かつ
$1.0 \verb|≦| \alpha \verb|≦| 1.5$とする。
$Q_{AS}$:短期許容せん断力
$f_s$:コンクリートの短期許容せん断応力度(N/mm2)
$_wf_t$:せん断補強筋の短期許容引張応力度(N/mm2)
$p_w$:せん断補強筋比(= $p_w/(b・x)$)
1.2%を超える場合は1.2%とする。
$a_w$:1組のせん断補強筋の断面積(mm2)
$x$:せん断補強筋の間隔(mm)
円形柱の場合、各寸法は以下のように扱います。
$D$ : 円形柱直径
$b$ = $D/2×√π$
せん断補強筋比 $p_w = a_w / (b・x)$
引張主筋本数 $n_t = n_g / 4 + 1 n_g$ : 全主筋本数
b) 柱の短期設計用せん断力( $Q_D$)
柱の短期設計用せん断力( $Q_D$)は、ユーザー選択注2)により $Q_{D1}$および $Q_{D2}$のいずれか、または小さいほうとします。 $$Q_{D} = \min (Q_{D1},Q_{D2})$$ $$Q_{D1} = \frac{\sum {_c}M_y}{h}$$ $$Q_{D2} = Q_L+n \cdot Q_E$$
$Q_D$:短期設計用せん断力
$Q_L$:長期設計用せん断力
$Q_E$:地震荷重によるせん断力
$n$:水平荷重時せん断力の割増係数で、1.5以上とする。
Σ $_cM_y$:柱頭・柱脚の降伏曲げモーメントの絶対値の和(= Σ$M_u$)
柱の曲げ終局強度( $M_u$)は"「鉄筋コンクリート造梁の終局耐力」“を参照してください。
$h$:柱の内法高さ
※積雪時、暴風時の短期設計用せん断力は以下とします。
・積雪時: $Q_D=Q_L+Q_{sn}$
・暴風時: $Q_D=Q_L+Q_w$
c) 高強度せん断補強筋を使用する場合について
■せん断補強筋比( $p_w$)
高強度せん断補強筋を使用する場合の、柱の許容せん断力( $Q_A$)算定に用いるせん断補強筋比( $p_w$)の制限値は梁と同じとします。
■許容せん断力( $Q_A$)
高強度せん断補強筋を使用する場合の許容せん断力( $Q_A$)は下式により算定します。
$$Q_{AL} =\alpha \cdot f_s \cdot b \cdot j$$ $$Q_{AS} = b \cdot j ( \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$$
$Q_{AL}$:長期許容せん断力
$Q_{AS}$:短期許容せん断力
【ウルボン1275の場合】
$$ Q_{AS} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \phi \cdot b \cdot D \cdot \left( 850 \cdot \sqrt{\frac{W_0}{D} \cdot \frac{p_W}{_L\sigma_0+3} }\cdot \frac{M}{Q \cdot D}+1 \right) \cdot _L\tau_{SC} & \displaystyle \left( \text{損傷制御のための検討} \right) \\ \displaystyle b \cdot j ( \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001)) & \displaystyle \left( \text{安全確保のための検討} \right) \end{array} \right. \end{align} $$ $W_0 = \frac{W_a}{3 \cdot Q_L/(Q_L+Q_E)+1}$$_L\tau_{SC}$ = $\sqrt{\sigma_T^2+\sigma_T \cdot {_L\sigma}_0}/\kappa$
・大梁の場合、 $Lσ_0=0$とします。
・ $M/(Q・D)$が2.0を超える場合は2.0とします。
・ $_Lσ_0$が0以下の場合、 $_Lτ_{SC}$ の算定では負として扱い、 $Q_{AS}$算定では0として扱います。
・ $_Lσ_0$が18N/mm2を超える場合、 $_Lσ_0$が18N/mm2とします。
また、損傷制御のための検討を選択していた場合でも、軽量コンクリートは対象外のため、安全性確保のための検討とします。
$f_s$は軽量コンクリートの場合、0.75倍とします。
【スーパーフープKH785,KH685の場合】
$$Q_{AL}=b・j(a・f_s+0.5・_wf_t(p_w-0.002))$$ $$ Q_{AS} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle b・j(β_c・a・f_s+0.5・_wf_t(p_w-0.002)) & \displaystyle \left( \text{損傷制御のための検討} \right) \\ \displaystyle b・j(a・f_s+0.5・_wf_t(p_w-0.002)) & \displaystyle \left( \text{安全確保のための検討} \right) \end{array} \right. \end{align} $$ $β_c:1-(100p_w-0.2)/3$$Q_{AL}$長期許容せん断力
$Q_{AS}$:短期許容せん断力
【パワーリング785の場合】
SPR785の損傷制御のための検討、安全性確保のための検討は下式で算定します。
$$ Q_{AS} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle b \cdot j \left( \frac{2}{3} \cdot \alpha_{s1} \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) \right) & \displaystyle \left( \text{損傷制御のための検討} \right) \\ \displaystyle b \cdot j ( f_s+0.5 \cdot {_w}f_t(p_w-0.001)) & \displaystyle \left( \text{安全確保のための検討} \right) \end{array} \right. \end{align} $$また、損傷制御のための検討を選択していた場合でも、長期荷重時に引張軸力が作用する柱部材については安全性確保のための検討で算定します。
【パワーリング685の場合】
SPR685の"損傷制御のための検討”、“安全性確保のための検討"は下式で算定します。
$$ Q_{AS} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle b \cdot j ( \beta_{co} \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001)) & \displaystyle \left( \text{損傷制御のための検討} \right) \\ \displaystyle b \cdot j ( f_s+0.5 \cdot {_w}f_t(p_w-0.001)) & \displaystyle \left( \text{安全確保のための検討} \right) \end{array} \right. \end{align} $$$β_{co}$は以下の式を用いるか、2/3αとするか選択できます。ただし、柱内法高さ比が2.5未満の場合、 $β_{co}=2/3α$とします。
$\beta_{co} = 1- ( 1-(2/3)\alpha ) (100p_w-0.2)$【エムケーフープの場合】
MK785の"損傷制御のための検討”、“安全性確保のための検討"は下式で算定します。
$$ Q_{AS} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle b \cdot j \left(\frac{2}{3} \cdot \alpha_{s1} \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) \right) & \displaystyle \left( \text{損傷制御のための検討} \right) \\ \displaystyle b \cdot j ( f_s+0.5 \cdot {_w}f_t(p_w-0.001) ) & \displaystyle \left( \text{安全確保のための検討} \right) \end{array} \right. \end{align} $$また、損傷制御のための検討を選択していた場合でも、長期荷重時に引張軸力が作用する柱部材については"安全性確保のための検討"で算定します。
【上記以外の高強度せん断補強筋の場合】
$$ Q_{AS} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle b \cdot j \left( \frac{2}{3} \cdot \alpha_{s1} \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) \right) & \displaystyle \left( \text{損傷制御のための検討} \right) \\ \displaystyle b \cdot j ( f_s+0.5 \cdot {_w}f_t(p_w-0.001) ) & \displaystyle \left( \text{安全確保のための検討} \right) \end{array} \right. \end{align} $$
※上式は暫定対応による計算となっています。メーカーの設計指針と計算内容が異なる場合があります。
注2) メインメニュー「設計・計算条件」→「断面算定条件」→「RC造」参照。
鉄筋コンクリート造耐震壁の断面検定
記号説明
$t$ :壁板の厚さ
$l$ :柱を含む壁部材の全せい
$h$ :壁板周辺の梁中心間距離
$l_0$ :開口部の長さ
$h_0$ :開口部の高さ
$l'$ :壁板の内法長さ
$l_e$ :壁の有効長さ
両側に柱がある場合、
$l_e$ = l’
片側に柱がある場合、
$l_e$ = 0.9 * l’
柱がない場合、
$l_e$ = 0.8 * l'
$h'$ :壁板の内法高さ
$p_s$ :壁板の直交する各方向のせん断補強筋比のうち小さい方の値
$f_s$ :コンクリートの短期許容せん断応力度
$p_w$ :帯筋比
$_wf_t$ :壁筋のせん断補強用短期許容引張応力度
$b$:柱幅
$d$ :柱の有効せい
$j$ :柱の応力中心間距離(=7/8dとする)
[壁のせん断に対する断面算定]
$Q_w$ :無開口壁板の壁筋が負担できる許容水平せん断力
$Q_c$ :壁板周辺の柱(1本)が負担できる許容水平せん断力
$r$ :開口低減率
$Q_E$ :地震荷重によるせん断力
$Q_{DW}$ :風荷重によるせん断力
$Q_D$ :短期設計用せん断力
$Q_D/Q_a$ :短期水平せん断力に対する検定値
せん断力に対する検討
壁の許容せん断力が設計せん断力以上であることを、以下により確認します。
$$Q_D/Q_a ≦ 1.0$$a) 壁の許容せん断力
長期許容せん断力は $Q_1$、短期許容せん断力は $Q_1$ と $Q_2$ の大きい方とします。
$$Q_a=Max(Q_1,Q_2)$$ $$ \begin{align} \left\lbrace \begin{array}{ll} \displaystyle Q_1=r・t・l・f_s \\ \displaystyle Q_2=r(Q_w+ΣQ_c) \end{array} \right. \end{align} $$無開口壁板の壁筋が負担できる許容水平せん断力 $Q_W$は次式によります
$$Q_w=p_s・t・l_e・_wf_t$$壁板周辺の柱1本が負担できる許容水平せん断力 $Q_C$は次式によります。
$$Q_c=b・j・(1.5f_s+0.5_wf_t(p_w-0.002))$$開口低減率 $\gamma$は次式によります。
$$r=Min(\gamma_1,\gamma_2,\gamma_3)$$ $$ \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \gamma_1 = 1-l_0/l \\ \displaystyle \gamma_2 = 1- \sqrt{h_0 \cdot l_0/h \cdot l} \\ \displaystyle \gamma_3 = 1-h_0/h \end{array} \right. \end{align} $$b) 壁の設計用せん断力
壁の設計用せん断力は地震荷重によるせん断力と、風荷重によるせん断力の大きい方とします。
$$Q_D=Max(Q_E,Q_{DW})$$鉄筋コンクリート造柱梁接合部の断面検定
記号説明
$κ_A$ :形状係数
$f_s$ :コンクリートの短期許容せん断応力度(N/mm2)
$_cD$ :柱せい (mm)
$_gB$ :梁幅 (mm)
$b_{a1},b_{a2}$:幅方向柱フェイスから梁フェイスまでの距離 (mm)
$b_j$ :大梁幅と有効幅の和 (mm)
$Q_{Aj}$ :許容せん断力(kN)
$g_{j1}$ :左側大梁の応力中心間距離 (mm)
$g_{j2}$ :右側大梁の応力中心間距離 (mm)
$_gL$ :大梁の平均スパン間距離 (mm)
$_cH$ :柱の平均階高 (mm)
$ξ$ :架構の形状に関する係数
$Q_{dj1}$ :大梁の降伏モーメントから算出されるせん断力(kN)
$Q_{dj2}$ :柱の設計用せん断力から算出されるせん断力(kN)
$Q_{dj} :min(Q_{dj1}, Q_{dj2})$ (kN)
せん断力に対する検討
柱梁接合部の許容せん断力は以下の式により計算します。
$Q_{Aj} = κ_A・(f_s - 0.5)・b_j・D$$κ_A$は柱梁接合部の形状による係数で以下とします。
$κ_A$ = $10$ (十字形接合部)
$κ_A$ = $7$(T字形接合部)
$κ_A$ = $5$ (ト字形接合部)
$κ_A$ = $3$ (L字形接合部)
$b_j$は柱梁接合部の有効幅で次式によります。
$b_j = b_b + b_{a1} + b_{a2}$$b_b$ :梁幅
$b_{ai}$ : $b_i / 2$ または $D / 4$の大きい方
$b_i$ :梁両側面から平行する柱側面までの長さ
$D$ :柱せい
設計用せん断力は下記のうち小さい方を採用します。
$Q_{dj1} = ΣM_y/j・(1 - ξ)$ $Q_{dj2} = Q_D・(1 - ξ) /ξ$ξは架構の形状に関する係数で下記によります。
$ξ= j / ( c_H・(1 - D / L_b) )$鉄筋コンクリート造梁付着の断面検定
記号説明
<鉄筋コンクリート構造計算規準・解説 1991>
$b$ :長方形梁の幅(mm)
$D$ :梁せい(mm)
$d_t$上 :鉄筋重心位置(上端引張)(mm)
$d_t$下 :鉄筋重心位置(下端引張)(mm)
$j$上 :応力中心間距離(上端引張)(mm)
$j$下 :応力中心間距離(下端引張)(mm)
$f_aL$ :長期許容付着応力度(N/mm2)
$f_aS$ :長期許容付着応力度(N/mm2)
$τ_a$ :設計用せん断応力度(N/mm2)
$σ_t$ :引張鉄筋継手部分の応力度(フックを設ける場合には2/3倍した値、N/mm2)
$l_d$ :付着検定断面からの付着長さ(mm)
必要長 :必要延長長さ
<鉄筋コンクリート構造計算規準・解説 1999>
$b$ :長方形梁の幅(mm)
$D$ :梁せい(mm)
d上 :有効せい(上端引張)(mm)
d下 :有効せい(下端引張)(mm)
$σ_t$ :引張鉄筋継手部分の応力度(フックを設ける場合には2/3倍した値、N/mm2)
$l_d$ :付着検定断面からの付着長さ(mm)
$l_{db}$ :必要付着長さ
検討方法(鉄筋コンクリート構造計算規準・解説 1991)
・検定断面位置は左端、左端カットオフ位置、右端カットオフ位置、右端とします。
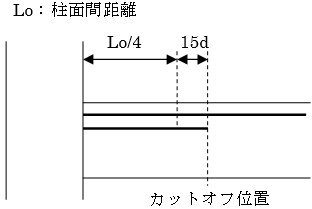
・カットオフ位置は柱面間距離の1/4から15d(指定により変更可能)中央側の位置とします。
・付着応力度の検定は以下の式により行います。
$τ_a=Q/φ_j≦f_a$
$Q$ :長期、短期荷重時の設計用せん断力
$j$ :曲げ材の応力中心間距離
$d$ :梁の有効せい
$φ$ :引張鉄筋の周長の総和
$f_a$ :許容付着応力度
・スパン途中の鉄筋端までの距離の検定は以下の式により行います。
$l_d≧σ_t・a/(0.8f_a・φ)+j$$l_d$ :算定位置から鉄筋端までの長さ(通し筋では反対側の柱面までの長さ)
$a$ :鉄筋断面積
$φ$ :鉄筋周長
$f_a$ :許容付着応力度
$j$ :曲げ材の応力中心間距離
検討方法(鉄筋コンクリート構造計算規準・解説 1999)
・検定断面位置は左端、左端カットオフ位置、中央、右端カットオフ位置、右端とします。
・カットオフ位置は以下のように設定します。
1.端部鉄筋が中央鉄筋より多い場合、柱面間距離の1/4から15d中央側の位置とします。
2.中央鉄筋が端部鉄筋より多い場合、柱面間距離の1/4から20d端部側の位置とします。
・付着長さldは以下のように設定します。
| 左端 | 1/4位置 | 中央 | 3/4位置 | 右端 | |
|---|---|---|---|---|---|
| カットオフ無し | (通し筋長さ+d)/2 | 算定しない | 通し筋長さ/2 | 算定しない | (通し筋長さ+d)/2 |
| カットオフ有り (端部が多い場合) | CL | 残りが通し筋: (Lo-CL+d)/2 それ以外:Lo-CL-CR+d | 算定しない | 残りが通し筋:(Lo-CR+d)/2 それ以外:Lo-CL-CR+d | CR |
| カットオフ有り (中央が多い場合) | 算定しない | CL+d (Cは中央断面からの距離) | (Lo/2-CL),(Lo/2-CR) の小さい方 | CR+d (Cは中央断面からの距離) | 算定しない |
$L_o$ :柱面間距離
$C$ :カットオフ位置(添え字L,Rはそれぞれ左端・右端)
$d$ :有効せい
・必要付着長さldbは以下のように計算します。
$l_{db}=σ_t・A_s/(K・f_b・φ)$
$σ_t$ :付着検定断面位置における鉄筋引張応力度
フックを設ける場合には2/3倍とする
$A_s$ :当該鉄筋の断面積
$φ$ :当該鉄筋の周長
$f_b$ :許容付着応力度(1段筋以外は0.6を乗じる)
$K$ :鉄筋配置と横補強筋による以下の修正係数
(長期荷重時) $0.3・C/d_b+0.4$
(短期荷重時) $0.3・(C+W)/d_b+0.4$
$d_b$ :曲げ補強鉄筋径
ただし、2.5を超える場合2.5とする
$C$ :鉄筋間のあき、最小かぶり厚さの3倍、鉄筋径の5倍のいずれか小さい値
$W$ :付着割裂面を横切る横補強筋効果を表す換算長さ
鉄筋径の2.5倍を超える場合は鉄筋径の2.5倍
$A_{st}$ :当該鉄筋列の想定される付着割裂面を横切る1組の横補強筋全断面積
$N$ :当該鉄筋列の想定される付着割裂面における鉄筋本数
$s$ :1組の横補強筋( $A_{st}$)の間隔
鉄筋コンクリート造水平接合面の検討
計算条件>断面算定計算条件>RC造条件2>水平接合面の検討にて「検討する」を選択した場合、「PCa」を選択した部材のみ水平接合面の検討を行います。
材軸平行接合部のせん断強度が、設計用せん断応力度を上回ることを確認します。
水平接合面で検定対象とする位置は、鉛直荷重時:両端上端、地震荷重時:上端引張となる端部のみとします(通常の応力状態では上端引張で決まるため)。
T形梁のスラブは、以下の条件とします。
- 鉛直荷重時使用限界状態検討における $S_y$算定時のスラブ幅は、異種強度梁の協力幅指定に従います(1-1.および1-2.参照)。
- スラブ厚は、計算条件>剛性計算条件>剛性条件1>各層スラブ厚の設定の値に従います。ただし、構造スラブがある場合は、構造スラブの厚さが優先されます。
- スラブ鉄筋は、計算条件>部材復元力特性計算条件>終局耐力条件2の「略算式スラブの設定」または「平面保持スラブの設定」にあるスラブ筋断面積を、T形梁の片側スラブ有効幅内にあるスラブ鉄筋とします。
使用限界状態における設計用せん断応力度
下式により求めます。
$\tau_{xy} = \frac{Q \cdot S_y}{b \cdot I}$ここで、
・
$Q$:部材断面に作用するせん断力
・
$S_y$:水平接合面より外側(断面縁側)のコンクリートの、図心位置からの断面一次モーメント
・
$b$:接合面の幅(梁幅)
・
$I$:T型梁の図心まわりの断面二次モーメント(応力計算で用いる値と同じものとします。ファイル>データ変換出力>csv出力>断面性能出力>大梁断面性能で確認できます。)
終局限界状態における設計用せん断応力度
下式により求めます。
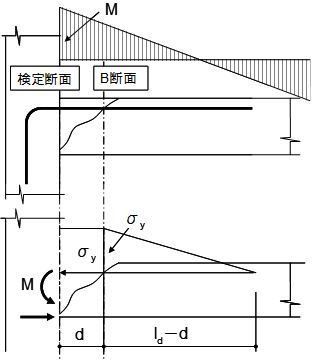
$\tau_{xy} = \frac{\Delta T}{b \cdot \Delta l}$ここで、
・
$\Delta T$:区間長さにおいて、水平接合面より外側(断面縁側)に含まれる引張鉄筋(T形梁ではスラブ鉄筋も含む)の応力変化量
・
$\Delta l$:区間長さ
区間長さ
$\Delta l$(現場打ち同等型プレキャスト鉄筋コンクリート構造設計指針(案)・同解説(2002)より)
$\Delta T$について、鉛直荷重に対する検討、地震時荷重に対する検討それぞれの算定方法を以下に示します。
- 鉛直荷重に対する検討:終局限界状態の設計用曲げモーメントを $M_d$, 梁の有効せいを $d$とすると、略算式より $\Delta T=M_d/(0.9d)$として求めます。
- 地震時荷重に対する検討:引張鉄筋の降伏耐力とします。ただし、上端引張の場合はスラブ鉄筋を含め、強度倍率(荷重・材料>材料強度>鉄筋の強度倍率と、計算条件>終局検定計算条件>終局検定条件3の標準上限強度倍率の重ね掛け)を考慮します。
ここで、
・
$M_d = \alpha \cdot M_{DL} + \beta \cdot M_{LL}$
・
$M_{DL}$:固定荷重に対する曲げモーメント
・
$M_{LL}$:積載荷重に対する曲げモーメント
・
$\alpha$,
$\beta$:それぞれ
$M_{DL}$,
$M_{LL}$に対する荷重倍率
$\Delta l$の算定方法は、端部から下式の2次曲線の $M=0$となる位置(近い方)までの距離とします。
$M = M_1 + \frac{-M_1 - M_2+4 \cdot M_0}{L} \cdot x - \cfrac{4 \cdot M_0}{L^2} \cdot x^2$ここで、
・
$M_1$,
$M_2$:端部モーメント,
$M_1$は下側引張を正,
$M_2$は上側引張を正とします(鉛直荷重時は、荷重倍率
$\alpha$,
$\beta=1.0$とした設計用モーメントとします。地震荷重時は、両端のヒンジ発生モーメントとします。)
・
$M_0$:単純梁の中央モーメント, 下側引張を正とします
・
$x$:採用応力位置
・
$L$:部材長
使用限界状態におけるせん断強度
下式により求めます。
$\tau_u = 0.5 \cdot \mu \cdot ( p_w \cdot \sigma_y + _{r}p_w \cdot _{r}\sigma_y ) = 0.5 \cdot \mu \cdot p_w' \cdot \sigma_y$ここで、
・
$\mu$:水平接合面の摩擦係数
・
$ p_w$:あばら筋の体積比
・
$ _{r}p_w $:補強筋の体積比
・
$\sigma_y$:あばら筋の降伏強度
・
$ _{r}\sigma_y$:補強筋の降伏強度
終局限界状態におけるせん断強度
下式により求めます。
$\tau_u = \mu \cdot ( p_w \cdot \sigma_y + _{r}p_w \cdot _{r}\sigma_y ) = \mu \cdot p_w' \cdot \sigma_y$鉄骨造梁の断面検定
記号説明
$A$ :全断面積
$A_w$ :ウェブ有効断面積
$Z$ :断面係数
$f_t$ :許容引張応力度
$f_b$ :許容曲げ応力度
$f_s$ :許容せん断応力度
$f_c$ :許容圧縮応力度
$σ_b$ :曲げ応力度
$σ_c$ :圧縮応力度
$τ$ :せん断応力度
$N$ :設計用軸力
$M$ :設計用曲げモーメント
$Q$ :設計用せん断力
曲げモーメント、せん断に対する検討
a) H形鋼全断面
端部
$σ_b=M/Z$ $τ=Q/(t_1・H)$$σ_b/f_b≦1.0$ :曲げ応力度比
$\frac{\sqrt{\sigma_b'^2+3\tau^2}}{f_t} \leq 1$ :せん断検定比(1) ここで、 $σ_{b'}=σ_{b×}(H - 2・t_2) / H$
$\frac{\tau}{f_s} \leq 1$ :せん断検定比(2)
max((1)式、(2)式) :せん断検定比
※指定により(2)のみとすることが可能です。
※許容曲げモーメント算定時にウェブを考慮しない場合には(2)で検定します。
中央
$σ_b=M/Z$$σ_b/f_b≦1.0$ (長期)
$\frac{\sqrt{\sigma_b'^2+3\tau^2}}{f_t} \leq 1$ :せん断検定比(1) ここで、 $σ_{b'}=σ_{b×}(H - 2・t_2) / H$
$\frac{\tau}{f_s} \leq 1$ :せん断検定比(2)
max((1)式、(2)式) :せん断検定比
※指定により(2)のみとすることが可能です。
※許容曲げモーメント算定時にウェブを考慮しない場合には(2)で検定します。
b) H形鋼(ウェブ非考慮)
曲げモーメント ・・・フランジ負担
せん断 ・・・ウェブ負担
端部
$σ_b=M/(h・B・t_2)$ $τ=Q/(t_1・H')$ $σ_b/f_b≦1.0$$\frac{\tau}{f_s} \leq 1$ :せん断検定比
中央
端部に同じ
c) 大梁必要横補剛数の算定
$n=(170-λ_y)/20$ (SS400級)
$n=(130-λ_y)/20$ (SM490級)
ただし、 $λ_y=L/i_y$ (梁の弱軸に関する細長比)
$i_y=√(l_y/A)$ (梁の弱軸に関する回転半径)
d) たわみ量の検定
梁中央部のたわみを次の仮定にしたがって計算します。
中央断面が部材全長にあると仮定します。
応力状態は元の荷重パターンに拘わらず等分布荷重を想定し、下図のようであると仮定します。中央のたわみSは下式により求めます。
e) 横座屈長さLbの計算方法
フランジの拘束条件を「横補剛材による拘束」としている場合、以下のように横座屈長さを計算します。
(1) 横座屈長さを直接入力した場合
- 始端:「始端横座屈長(mm)」の値
- 始端側ジョイント位置:「中央座屈長(mm)」の値
- 中央:「中央座屈長(mm)」の値
- 終端側ジョイント位置:「中央座屈長(mm)」の値
- 終端:「終端横座屈長(mm)」の値
(2) 横座屈長さ自動計算の場合(直接入力していない場合)
- 始端:始端からL/4位置までの横補剛間隔の内、最大のもの
- 始端側ジョイント位置:始端からL/4位置の横補剛間隔
- 中央:部材中心から両端にL/4位置までの補剛間隔の内、最大のもの
- 終端側ジョイント位置:始端から3L/4位置の横補剛間隔
- 終端:3L/4位置から終端までの横補剛間隔の内、最大のもの
始端の横座屈長さ計算の例
中央の横座屈長さ計算の例
終端の横座屈長さ計算の例
鉄骨造柱の断面検定
記号説明
$A$ :全断面積
$A_w$ :ウェブ有効断面積
$Z$ :断面係数
$f_t$ :許容引張応力度
$f_b$ :許容曲げ応力度
$f_s$ :許容せん断応力度
$f_c$ :許容圧縮応力度
$σ_b$ :曲げ応力度
$σ_c$ :圧縮応力度
$τ$ :せん断応力度
$N$ :設計用軸力
$M$ :設計用曲げモーメント
$Q$ :設計用せん断力
軸力と曲げモーメントに対する検討
a) H形鋼
$σ_c=N/A$ :圧縮応力度
$σ_{bX}=M_X/Z_y$ :曲げ応力度
$σ_{bY}=M_Y/Z_x$$τ=Q/(t_1・H)≦f_s$ :せん断応力度
$σ_c/f _c+σ _{bX}/f _b+σ _{bY}/f _b≦1.0$強軸まわりは、必ず横座屈( $l_b$)を考慮したfb、弱軸まわりは $f_b=f_t$
$l_b$は階高とします
b) 角形鋼管
$σ_c=N/A$ $σ_{bX}=M_X/Z_y$ $σ_{bY}=M_Y/Z_x$ $τ=2Q/A$ $σ_c/f_c+σ_{bX}/f_b+σ_{bY}/f_b≦1.0$$f_b=f_t$とします。
c) 鋼管
$σ_c=N/A$ $cσ_b = (M_{X}^2 + M_{Y}^2)^{1/2} /Z_c$$tσ_b $ = $(M_{X}^2 + M_{Y}^2)^{1/2} /Z_t$
$τ=2(Q_{X^2}+Q_{Y^2})^{1/2}/A$ $σ_c/f_c+σ_b/f_b≦1.0$せん断に対する検討
$\frac{\sqrt{\sigma^2+3\tau^2}}{f_t} \leq 1$ …(1)
$\frac{\tau}{f_s} \leq 1$ …(2)
a) H形断面の場合
・曲げ許容応力度にウェブを考慮する場合
検定値は(1)または(2)の大きい方とします。
その際、 $σ=σ_c+σ_{b'}、σ_{b'}=σ_{b×}(H -- 2・t2) / H$とします。
・曲げ許容応力度にウェブを考慮しない場合
検定値は(2)とします。
b) それ以外の断面の場合
検定値は(1)または(2)の大きい方とします。
その際、 $σ=σ_c+σ_{bx}+σ_{by}$とします。
柱の座屈長さ係数は、「鋼構造塑性設計指針」(6.65)~(6.67)式により、水平移動が拘束されない場合の座屈長さ係数Kを求めます。
座屈長さ係数は、以下の式より求めます。
$\frac{G_AG_B(\pi /K)^2-36}{6(G_A+G_B)} = \frac{\pi /K}{\tan (\pi /K)}$G:節点に集まる柱と梁の剛度の比
$G = \frac{\sum (l_c/l_c)}{\sum (l_g/l_g)}$添え字のA,Bは、柱の両端の節点を示します。
柱端がピン接合の場合は、G=10とします。
節点に接する梁が無い場合は、G=10とします。
混合構造の場合、節点に接する部材の構造種別がRC造またはSRC造のときは、その部材の剛性をヤング係数比により補正して計算します。
節点に接する部材の角度は考慮していません。
一本部材の指定は考慮していません。
梁の結合状態および支点の状態は考慮していません。
$I$:断面2次モーメント 添え字cは柱、gは梁
$l$:部材の長さ 添え字cは柱、gは梁
特殊形状による材長を考慮します。
$∑$:節点に集まる部材についての和
幅厚比の検討
a) 部材ランクの検討 ※部材ランク検討機能は現状では一部対応となります。
構造規定の幅厚比により、部材ランクを検討します。
| 部材 | 断面 | 部位 | 鋼種 | FA | FB | FC | FD |
|---|---|---|---|---|---|---|---|
| 柱 | H型鋼 | フランジ | 400N/mm2級 490N/mm2級 | 9.5 8 | 12 10 | 15.5 13.2 | 左記以外 |
| ウェブ | 400N/mm2級 490N/mm2級 | 43 37 | 45 39 | 48 41 | |||
| 円形鋼管 | - | 400N/mm2級 490N/mm2級 | 50 36 | 70 50 | 100 73 | ||
| 角形鋼管 | - | STKR400 | 33 | 37 | 48 | ||
| - | STKE490 | 27 | 32 | 41 | |||
| - | BCR295 | 30 | 34 | 43 | |||
| - | BCP235 | 33 | 37 | 48 | |||
| - | BCP325 | 27 | 32 | 41 | |||
| 梁 | H型鋼 | フランジ | 400N/mm2級 490N/mm2級 | 9 7.5 | 11 9.5 | 15.5 13.2 | |
| ウェブ | 400N/mm2級 490N/mm2級 | 60 51 | 65 55 | 71 61 |
幅厚比の検討式、およびb、dの取り方を以下に示します。
| 断面 | 部位 | 検討式 | |
|---|---|---|---|
| H形鋼 | フランジ | $\frac{b}{t_2}$ | $b=\frac{B}{2}$ |
| ウェブ | $\frac{d}{t_1}$ | $d=H-2t_2$ | |
| 角形鋼管 | - | $\frac{d}{t}$ | $d=H$ |
| 鋼管 | - | $\frac{d}{t}$ | $d=D$ |
鉄骨造パネルゾーンの断面検定
鉄骨造の柱梁接合部は「鋼構造接合部設計指針」を参考に接合部パネルの検討を行います。
※ 検討結果はCSV出力のみ対応しています。メニュー「ファイル」→「データ変換出力」→「CSV出力」→「断面検定情報/断面検定表/柱梁接合部/S」から出力できます。
設計用パネルモーメント
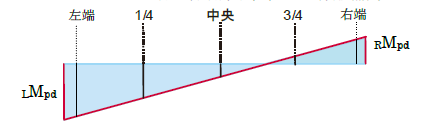
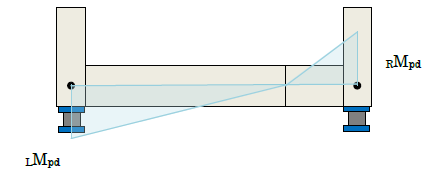
接合部パネルモーメントは接合部に取り付く梁せいの差によって以下のように計算方法を切り替えます。
・梁せい差が150mm未満のときは標準形式として計算
・梁せい差が150mm以上のときは梁段違い形式として計算
[標準形式]
$_pM$ = ${_b}M_L+{_b}M_R-({_c}Q_U+{_c}Q_L) \cdot \frac{d_b}{2}$
$_bM_L$ : 接合部パネルの左側大梁のフェイスモーメント
$_bM_R$ : 接合部パネルの右側大梁のフェイスモーメント
$_cQ_U$ : 接合部パネルの上側柱のせん断力
$_cQ_L$ : 接合部パネルの下側柱のせん断力
$d_b$ : 梁フランジの板厚中心間距離
[梁段違い形式]
$ _pM $ = $ _ bM_H \cdot \left( \frac{d_{bL}}{d_{bH}} \right) +{_b}M_L-({_c}Q_U+{_c}Q_L) \cdot \frac{d_{bL}}{2} $
$_bM_H$ : 接合部パネルの梁せいが低い側の大梁のフェイスモーメント
$_bM_L$ : 接合部パネルの梁せいが高い側のフェイスモーメント
$_cQ_U$ : 接合部パネルの上側柱のせん断力
$_cQ_L$ : 接合部パネルの下側柱のせん断力
$d_{bH}$ : 梁せいが高い側の梁フランジの板厚中心間距離
$d_{bL}$ : 梁せいが低い側の梁フランジの板厚中心間距離
接合部パネル降伏モーメント
$_pM_y = \frac{V_e}{\kappa} \sqrt{(1-n^2)}\frac{Fy}{\sqrt{3}}$$F_y$ : 接合部パネルの降伏強さ
上下に柱が存在する場合は下側柱、存在しない場合は存在する柱の降伏強さを採用します。
$n$ : 軸力比 $n = N / (F_y・A)$
$N$ : 上下階の柱軸力の平均値+ブレース軸力の鉛直方向成分
$V_e$ : 接合部パネルの有効体積
$κ$ : 形状係数
$A$ : 接合部パネルの断面積
ここで、 $V_{e,κ}$は以下の数式により算出します。
| Ve | κ | |
|---|---|---|
| H | $V_e=d_c \cdot d_b \cdot t_p$ | $\kappa =\frac{1}{\frac{2}{3}+\frac{4b_c \cdot t_f}{d_c \cdot t_p}}+\frac{1}{1+\frac{d_c \cdot t_p}{6b_c \cdot t_f}}$ |
| 角型鋼管 | $V_e=2d_c \cdot d_b \cdot t_p$ | $\kappa =\frac{1}{\frac{2}{3}+\frac{2b_c}{d_c}}+\frac{1}{1+\frac{d_c}{3b_c}}$ |
| 円形鋼管 | $V_e=2d_c \cdot d_b \cdot t_p$ | $\kappa =\frac{4}{\pi}$ |
冷間成形角型鋼管の断面検定
冷間成形角型鋼管を用いた場合、「2008年版冷間成形角型鋼管設計・施工マニュアル」に基づき、柱梁耐力比および柱パネル耐力比のチェックを行います。チェックでNGとなった場合でも耐力の低減は行いません。なお、2次設計時の軸力比の計算における存在軸力は,地震時軸力 $N_E$に $D_s/C_o=1.5$ を乗じて長期軸力 $N_L$ に加算した値とします。
■耐力比のチェック
$\sum M_{pc} \verb|≧| \sum \min ( 1.5M_{pb},1.3M_{pp} )$ $\sum M_{pc} = M_{pcu}+M_{pcl} $ $\sum M_{pb} = M_{pbl}+M_{pbr}$ $\sum M_{pcu} = \nu_u \cdot F_{yu}+Z_{pcu} $ $\sum M_{pcl} = \nu_l \cdot F_{yl}+Z_{pcl} $ $\nu_u,\nu_l = (1-4n^2/3) \quad (n \leq 0.5)$ $\nu_u,\nu_l = 4(1-n)/3 \quad (n 0.5)$$n$ :軸力比
$F_{yu},F_{yl}$ :上側、下側柱の材料基準強度
$Z_{yu},Z_{yl}$ :上側、下側柱の塑性断面係数
■大梁耐力
$\sum M_{pbl} = F_{ybl} \cdot Z_{pbl}$ $\sum M_{pbu} = F_{ybu} \cdot Z_{pbu} $$F_{ybu}, F_{ybl}$ :左側、右側大梁の材料基準強度
$Z_{pbu}, Z_{pbl}$ :左側、右側大梁の塑性断面係数
■パネル耐力
$M_{pp} = V_e \frac{F}{\sqrt{3}} \quad (n \leq 0.5)$ $M_{pp} = V_e \frac{F}{\sqrt{3}} 2 \sqrt{n(1-n)} \quad (n0.5)$ $Ve = 2 \cdot d_c \cdot d_b \cdot t_p$$F$:パネル材の材料基準強度
$d_c$:パネル部フランジ板厚中心間距離
$d_b$:梁フランジ板厚中心間距離
$t_p$:パネル板厚
$n$:パネル軸力比(上柱、下柱軸力の平均から計算する)
CFT柱の断面検定
(1) 記号説明
$L_k$ :柱の座屈長さ(mm)
$K$ :柱の座屈長さ係数
$λ$ :鉄骨の細長比(=i/Lk) $i$:断面二次半径
$_sZ$ :鉄骨の断面係数(cm3)
$_SA$ :鉄骨部分の断面積(cm2)
$_SA_W$ :鉄骨部分のせん断有効断面積(cm2)
$_CA$ :コンクリート部分の断面積(cm2)
$x_{n1}, x_{n2}$ :曲げ材の圧縮縁から中立軸までの距離(mm)
$_CA$ :コンクリート部分の断面積(cm2)
$F_C(_CF_C)$:コンクリートの設計基準強度(N/mm2)
相互拘束効果を考慮する場合は、拘束効果を考慮したコンクリートの設計基準強度( $_CF_C$)を示します。
$_Sf_C$ :鉄骨の短期許容圧縮応力度(N/mm2)
$_Sf_C'$ :軸力制限検討時の鉄骨の短期許容圧縮応力度(N/mm2)
柱頭と柱脚の $_Sf_C$のうちで小さい方を採用します。
内法/ $D$ :内法長さに対する柱せい( $D$)の比
$L_k/D$ :柱の座屈長さ( $L_k$)に対する柱せい(D)の比
[曲げに対する断面算定]
$_CN$ :コンクリート部分の短期許容圧縮力(kN)
$_SN$ :鉄骨部分の短期許容圧縮力(kN)
$_CM_1,_CM_2$:コンクリート部分の短期許容曲げモーメント(kN・m)
$_SM$ :鉄骨部分の短期許容曲げモーメント(kN・m)
$M_{aL}$ :全体の長期許容曲げモーメント(kN・m)
$M_{aS1},M_{aS2}$ :全体の短期許容曲げモーメント(kN・m)
$_SM/M$ :鉄骨部分の曲げ負担率(=SM/max(MaS1,MaS2) )
$M_L/M_{aL}$ :長期曲げ検定値*1
$M_{s1}/M_{aS1}, M_{S2}/M_{aS2}$ :短期曲げ検定値*1
[せん断力に対する断面算定]
$Q_D$ :設計用せん断力(kN)
$_SQ _{aL}$ :鉄骨部分の長期許容せん断力(kN)
$_SQ _{aS}$ :鉄骨部分の短期許容せん断力(kN)
$Q_L/_SQ _{aL}$ :長期せん断検定値*1
$Q_D/_SQ _{aS}$ :短期曲げ検定値*1
*1:検定値は許容応力に対する設計用応力の比とします。
(2) CFT柱の断面検討
CFT柱の $f_c$低減は行いません(相互拘束効果を考慮しません)。
曲げモーメント $M_a$は単純累加強度式とします。
a) 軸力および曲げモーメントに対する検討
設計用軸力、曲げモーメントが許容耐力を下回ることを確認します。許容耐力は、SRC規準に基づいてコンクリート部分と鉄骨部分の累加(累加強度式)により算定します1)。
検定値は、二軸曲げを考慮して以下のように計算します。
$|_xM / _xM_a| + |_yM / _yM_a| ≦ 1.0$$_xM$ : X方向曲げモーメント
$_yM$ : Y方向曲げモーメント
$_xM_a$ : X方向曲げ許容モーメント
$_yM_a$ : Y方向曲げ許容モーメント
■ $0≦N≦_CN_C$または $M≧_SM_0$のとき
$N=_CN$
$M≦_SM+_CM$
■ $N>_CN$または $M<_SM_0$のとき
$N=_CN+_SN$
$M=_SM$
■N<0のとき
$N≧_sN$
$M=_SM$
ここで、
$N$:設計用圧縮力
$_CN_C$:コンクリート部分が圧縮力のみを受けたときの許容圧縮力
$_CN_C=_CA×f_c'$
$f_c'$:コンクリートの許容圧縮応力度(相互拘束効果は考慮しません。)
$_CN$:コンクリート部分の許容圧縮力
$_SN$:鉄骨部分の許容圧縮力
$M$:設計用曲げモーメント
$_sM_0$:鉄骨部分が曲げモーメントのみ受けたときの許容曲げモーメント
$_SM_0=_SZ×_Sf_t$
$_Sf_t$:鉄骨の短期許容引張応力度
$_CM$:コンクリート部分の許容曲げモーメント
$_SN$:鉄骨部分の許容曲げモーメント
■充填コンクリートの許容曲げモーメント
① 円形断面の場合
・中立軸が断面内の場合
$ \frac{_cN}{_cD^2 \times f_c} = \frac{1}{8X_n} \left(\frac{1}{3} \sin \theta(2+ \cos ^2\theta)-\theta \cos \theta \right)$ $ \frac{_cM}{_cD^3 \times f_c} = \frac{1}{64X_n} \left(\theta+ \frac{1}{3} \sin 2\theta \left( \cos ^2\theta-\frac{5}{2} \right) \right)$ $ \theta = \cos ^{-1}(1-2X_n)$・中立軸が断面外の場合( $e=_CM/_CN,e≦D/8$の場合)
$ \frac{_cN}{_cD^2 \times f_c} = \frac{\pi}{4} \left(1-\frac{1}{2X_n} \right)$ $ \frac{_cM}{_cD^3 \times f_c} = \frac{\pi}{64} \times \frac{1}{X_n} $② 矩形断面の場合
・中立軸が断面内の場合
$ \frac{_cN}{_cB \times _cD \times f_c} = \frac{1}{2}X_n$ $ \frac{_cM}{_cB \times _cD^2 \times f_c} = \frac{X_n}{12}(3-2X_n)$・中立軸が断面外の場合(e=CM/CN,e≦D/6の場合)
$ \frac{_cN}{_cB \times _cD \times f_c} = 1- \frac{1}{2X_n}$ $ \frac{_cM}{_cB \times _cD^2 \times f_c} = 1- \frac{1}{12X_n}$ここで、
$_CB$:コンクリート部分の柱幅
$_CD$:コンクリート部分の柱せい
$X_n$:柱のコンクリート部分の中立軸比(=xn/CD)
$x_n$:曲げ材の圧縮縁から中立軸までの距離
$f_c$:コンクリートの許容圧縮応力度(相互拘束効果を考慮しない値)
■鋼管部分の許容曲げモーメント
① $_SN$が圧縮力の場合
$ \frac{_sN}{_sA}+ \frac{_sM}{_sZ} = {_s}f_c $② $_SN$が引張力の場合
$ \frac{_sN}{_sA}- \frac{_sM}{_sZ} = {_s}f_t $ここで、
$_Sf_C$:鉄骨の許容圧縮応力度
$_Sf_t$:鉄骨の許容引張応力度
b) せん断力に対する検討
設計用せん断力が許容耐力を下回ることを確認します。
■許容せん断力
$_sQ_a = {_s}A_w \times _sF_s$$_SA_W$:せん断有効断面積
$_Sf_S$:鉄骨の許容せん断応力度
鉄骨鉄筋コンクリート造梁の断面検定
記号説明
$b$ :コンクリート梁幅(mm)
$D$ :コンクリート梁せい(mm)
$d_t$ :引張縁から引張鉄筋重心までの距離(mm)
$l$ :部材長、内法(mm)
$M_L$ :長期設計用曲げモーメント(kN・m)
$M_{sn}$ :積雪荷重による曲げモーメント(kN・m)
$M_{E1}$ :正加力時の地震荷重による曲げモーメント(kN・m)
$M_{E2}$ :負加力時の地震荷重による曲げモーメント(kN・m)
$M_s$ :短期設計用曲げモーメント(kN・m)
$_sZ$ :鉄骨の断面係数(mm3)
$M_{E1}$:正加力時の地震荷重による曲げモーメント(kN・m)
$M_{E2}$ :負加力時の地震荷重による曲げモーメント(kN・m)
$_sM_A$ $_L$ :鉄骨部分の長期許容曲げモーメント(kN・m)
$sM_A$ $_S$ :鉄骨部分の短期許容曲げモーメント(kN・m)
$_ra_t$ :引張鉄筋の断面積(mm2)
$rM_A$ $_L$ :鉄筋コンクリート部分の長期許容曲げモーメント(kN・m)
$rM_A$ $_S$ :鉄筋コンクリート部分の短期許容曲げモーメント(kN・m)
$M_A$ $_L$ :長期許容曲げモーメント(=sMAL+rMAL)(kN・m)
$M_A$ $_S$ :短期許容曲げモーメント(=sMAS+rMAS)(kN・m)
$M_L/M_A$ $_L$ :長期曲げモーメントの検定値
$M_S/M_A$ $_S$ :短期曲げモーメントの検定値
$Q_L$ :長期荷重によるせん断力(kN)
$Q_{sn}$ :積雪荷重によるせん断力(kN)
$Q_E$ :地震荷重によるせん断力(kN)
$Q_W$ :風荷重によるせん断力(kN)
$p_w$ :せん断補強筋比(%)
$α_L$ :長期のせん断スパン比による割り増し係数
$α_{S1}$ :短期正加力時のせん断スパン比による割り増し係数
$α_{S2}$ :短期正加力時のせん断スパン比による割り増し係数
$_rM_u$ :鉄筋コンクリート部分の終局曲げ強度(kN・m)
$_sZ_p$ :鉄骨の塑性断面係数(mm3)
$_sM/M$ :鉄骨部分の曲げ負担率
$_sM$:鉄骨部分の許容曲げモーメント
(= $_sM _{AL}$ または $_sM _{AS}$)(kN・m)
$M$:設計用曲げモーメント(kN・m)
$_sQ_L$ :鉄骨部分の長期設計用せん断力(kN)
$_sQ_D$ :鉄骨部分の短期設計用せん断力(kN)
$_rQ_L$ :鉄筋コンクリート部分の長期設計用せん断力(kN)
$_rQ_D$ :鉄筋コンクリート部分の短期設計用せん断力(kN)
$_sQ _{AL}$ :鉄骨部分の長期許容せん断力(kN)
$_sQ _{AD}$ :鉄骨部分の短期許容せん断力(kN)
$_rQ _{AL}$ :鉄筋コンクリート部分の長期許容せん断力(kN)
$_rQ _{AD}$ :鉄筋コンクリート部分の短期許容せん断力(kN)
曲げモーメントに対する検討
設計用曲げモーメントが許容曲げモーメントを下回ることを、以下の検定式による確認します。
$ M_L/M_{AL} \verb|≦| 1.0 $ (長期曲げモーメントの検定)
$ M_S/M_{AS} \verb|≦| 1.0 $ (短期曲げモーメントの検定)
a) 許容曲げモーメント(単純累加式)
許容曲げモーメントは、鉄筋コンクリート部分と鉄骨部分の累加(単純累加式)により算定します。
$M_A = {_s}M_o+{_r}M_A$$M_A$:許容曲げモーメント(N・mm)
$_sM_0$:鉄骨部分の許容曲げモーメント(N・mm)
${_s}M_o = {_s}Z \cdot {_s}f_t$
$_sf_t$:鉄骨の許容引張応力度(N/mm2)
$_rM_A$:鉄筋コンクリート部分の許容曲げモーメント(N・mm)
${_r}M_A = a_t \cdot f_t \cdot j$
$f_t$:主筋の許容引張応力度(N/mm2)
j:応力中心間距離(=7/8・d)(mm)
d:有効せい(= $D-d_t$)(mm)
せん断力に対する検討
設計用せん断力が許容せん断力を下回ることを、次式により確認します。
$_sQ_L$ $\verb|≦|$ $_sQ _{AL} $ および $_rQ_L \verb|≦| _rQ _{AL} $ (長期せん断力の検定)
$_sQ_D$ $\verb|≦|$ $_sQ _{AD} $ および $_rQ_D$ $\verb|≦|$ $_rQ _{AD} $ (短期せん断力の検定)
a) 許容せん断力【SRC規準】
鉄骨および鉄筋コンクリート部分の許容せん断力はSRC規準により算定します1)。
鉄骨部分の許容せん断力( $_sQ_A$)は下式により求めます。
${_s}Q_A = t_w \cdot d_w \cdot {_s}f_s$$t_w$:鉄骨のウェブ厚さ(mm)
$d_w$:鉄骨ウェブのせい( $=H-2・t_f$)(mm)
$_sf_s$:鉄骨の許容せん断応力度(N/mm2)
鉄筋コンクリート部分の許容せん断力( $_rQ_A$)は下式によります。
$_rQ_A$ = $min$ ( $_rQ _{A1} $, $_rQ _{A2} $)
$_rQ _{A1} $ = $b \cdot {_r}j \cdot ({_r}a \cdot f_s+0.5 \cdot p_w \cdot {_w}f_t)$
$_{r}Q _{A2}$ = $b \cdot _rj \cdot \left( 2 \cdot \frac{b'}{b} \cdot f_s+p_w \cdot _wf_t \right)$
$_rj$:鉄筋コンクリート部分の圧縮側と引張側の応力中心間距離(=7/8・ $_rd$)(mm)
$_rd$:有効せい(圧縮縁から引張主筋重心までの距離)(mm)
$_ra$: せん断スパン比による割増係数
( $α_L$, $α_{S1}$, $α_{S2}$)
$ _ra = \frac{4}{_rM/(_rQ \cdot _rd)+1} $ かつ $ 1 \verb|≦| _ra \verb|≦| 2 $
$_rM$:鉄筋コンクリート部分の設計用曲げモーメント(N・mm)
左端、中央、右端の設計用曲げモーメントのうちの最大値とする。
$_rQ$:鉄筋コンクリート部分の設計用せん断力(N)
左端、右端の設計用せん断力のうちの大きいほうとする。
$f_s$:コンクリートの許容せん断応力度(N/mm2)
$p_w$:あばら筋比( $=a_w/(b・x)$)(小数)
$p_w$が0.6%を超える場合は0.6%として算定する。
$a_w$:1組のあばら筋の断面積(mm2)
$x$:あばら筋の間隔(mm)
$_wf_t$:あばら筋のせん断補強用許容引張応力度(N/mm2)
$b'$:鉄骨フランジ位置でのコンクリートの有効幅(mm)
$b'$=コンクリート梁幅(b)-鉄骨フランジ幅(B)
b) 設計用せん断力
【構造規定】
SRC大梁設計用せん断力決定方法を「構造規定」とした場合、鉄骨部分および鉄筋コンクリート部分の設計用せん断力は以下により算定します2)。
■長期設計用せん断力
鉄骨部分の長期設計用せん断力( $_sQ_L$)、鉄筋コンクリート部分の長期設計用せん断力( $rQ_L$)は次式により算定します。
$ _sQ_L = \frac{_sZ}{_sZ+_ra_t \cdot _r j} \cdot Q_L $ (鉄骨部分)
$ _rQ_L = \frac{_ra_t \cdot _r j}{_sZ+_ra_t \cdot _r j} \cdot Q_L $ (鉄筋コンクリート部分)
■短期設計用せん断力
鉄骨部分の短期設計用せん断力( $_sQ_D$)、鉄筋コンクリート部分の短期設計用せん断力( $rQ_D$)は次式により算定します。
$_sQ_D$ = ${_s}Q_L$ + $\frac{_sM_1+_sM_2}{l'}$ (鉄骨部分)
$_rQ_D$= $min$ ( $_rQ _{D1}$, $_rQ _{D2}$) (鉄筋コンクリート部分)
$_rQ _{D1}$ = $_rQ_L$ + $ \frac{_rM_1+_rM_2}{l'}$
$ _rQ _{D2}$ = $n \cdot (Q_L+Q_E-{_s}Q_D) $
$_sM_1$:鉄骨部分の一端の短期許容曲げモーメント(N・mm)
$_sM_2$:鉄骨部分の他端の短期許容曲げモーメント(N・mm)
$l'$:梁の内法スパン(mm)
$_rM_1$:鉄筋コンクリート部分の一端の終局曲げモーメント(N・mm)
$_rM_2$:鉄筋コンクリート部分の他端の終局曲げモーメント(N・mm)
$n$:割増係数
積雪時、暴風時においては、長期および短期設計用せん断力算定式の $Q_L$を $Q_L+QSn、Q_L+Q_W$に置き換えて求めます。
【SRC規準】
SRC大梁設計用せん断力決定方法を「SRC規準」とした場合、鉄骨部分および鉄筋コンクリート部分の設計用せん断力は以下により算定します2)。
■長期設計用せん断力
鉄骨部分の長期設計用せん断力( $_sQ_L$)、鉄筋コンクリート部分の長期設計用せん断力( $_rQ_L$)は次式により算定します。
$_sQ_L = \frac{_sM_d}{M_L} \cdot Q_L$ (鉄骨部分)
$_rQ_L = \frac{_rM_d}{M_L} \cdot Q_L$ (鉄筋コンクリート部分)
ここで、 $ _sM_d = {_s}M_o $ 、 $ _rM_d = M_L-{_s}M_d $
■短期設計用せん断力
鉄骨部分の短期設計用せん断力( $_sQ_D$)、鉄筋コンクリート部分の短期設計用せん断力( $_rQ_D$)は次式により算定します。
$ _sQ_D = \frac{_sM_d}{M_S} \cdot (Q_L+Q_E) $ (鉄骨部分)
ここで、 $ _sM_d = {_s}M_o $ 、 $ _rM_d = M_S-{_s}M_d $
1) 日本建築学会:鉄骨鉄筋コンクリート構造計算規準・同解説;P.14-16,1987.6
2) 国土交通省:2007年版建築物の構造関係技術基準解説書;P.664-665,2007.8
鉄骨鉄筋コンクリート造柱の断面検定
記号説明
$b$ :柱の幅(mm)
$D$ :柱のせい(mm)
$d_t$ :引張縁から引張鉄筋重心までの距離(mm)
$l$ :部材長、内法(mm)
位置 :断面算定位置(mm)
$_ra_t$ :引張鉄筋の断面積(mm2)
$β$ :鉄骨ウェブ材の形式と寸法による係数
$α'$ : $α、b'/b$によって決まる係数
$M_L$ :長期設計用曲げモーメント(kN・m)
$M_{sn}$ :積雪荷重による曲げモーメント(kN・m)
$M_{E1}$ :正加力時の地震荷重による曲げモーメント(kN・m)
$M_{E2}$ :負加力時の地震荷重による曲げモーメント(kN・m)
$M_{W1}$ :正加力時の風荷重による曲げモーメント(kN・m)
$M_{W2}$ :負加力時の風荷重による曲げモーメント(kN・m)
$M_{s1}$ :正加力時の短期設計用曲げモーメント(kN・m)
$M_{s2}$ :負加力時の短期設計用曲げモーメント(kN・m)
$_rM_A$ $_L$ :鉄筋コンクリート部分の長期許容曲げモーメント(kN・m)
$_sM_A$ $_L$ :鉄骨部分の長期許容曲げモーメント(kN・m)
$M_{AL}$ :長期許容曲げモーメント(= $_{s}M_{AL}$+ $_rM _{AL}$)(kN・m)
$_rM _{AS}$ :鉄筋コンクリート部分の短期許容曲げモーメント(kN・m)
$_sM _{AS}$ :鉄骨部分の短期許容曲げモーメント(kN・m)
$M_{AS}$ :短期許容曲げモーメント(= $_sM_{AS}$+ $_rM_{AS}$)(kN・m)
$_rM_u$ :鉄筋コンクリート部分の終局曲げモーメント(kN・m)
$M_L/M_{AL}$ :長期曲げモーメントの検定値
$M_S/M_{AS}$ :短期曲げモーメントの検定値
$N_L$ :長期設計用圧縮力(kN)
$N_{sn}$ :積雪荷重による圧縮力(kN)
$N_{E1}$ :正加力時の地震荷重による圧縮力(kN)
$N_{E2}$ :負加力時の地震荷重による圧縮力(kN)
$N_{w1}$ :正加力時の風荷重による圧縮力(kN)
$N_{w2}$ :負加力時の風荷重による圧縮力(kN)
$N_{s1}$ :正加力時の短期設計用圧縮力(kN)
$N_{s2}$ :負加力時の短期設計用圧縮力(kN)
$_rN_L$ :鉄筋コンクリート部分の長期許容圧縮力(kN)
$_sN_L$ :鉄骨部分の長期許容圧縮力(kN)
$_rN_s$ :鉄筋コンクリート部分の短期許容圧縮力(kN)
$_sN_s$ :鉄骨部分の短期許容圧縮力(kN)
$Q_L$ :長期荷重によるせん断力(kN)
$Q_{sn}$ :積雪荷重によるせん断力(kN)
$Q_E$ :地震荷重によるせん断力(kN)
$Q_W$ :風荷重によるせん断力(kN)
$Q_s$ :短期設計用せん断力(kN)
$_sQ_D$ :鉄骨部分の短期設計用せん断力(kN)
$_rQ_D$ :鉄筋コンクリート部分の短期設計用せん断力(kN)
$Q_{AL}$ :長期許容せん断力(kN)
$_sQ _{AD}$ :鉄骨部分の短期許容せん断力(kN)
$_rQ _{AD}$ :鉄筋コンクリート部分の短期許容せん断力(kN)
軸力および曲げモーメントに対する検討
a) 軸力および曲げモーメントに対する検討
設計用軸力および曲げモーメントが許容耐力を下回ることを、以下の検定式により確認します1)。許容耐力については、鉄筋コンクリート部分と鉄骨部分の累加(累加強度式)により算定します。
■ $_rN_t≦N≦_rN_c$または $M≧_sM_0$のとき
$N=_rN$
$M≦_sM_0+_rM$
■ $N>_rN_cまたはM<_sM_0$のとき
$N=_rN_c+_sN$
$M=_sM$
■ $N<_rN_c$または軸方向力が引張で $M<_sM_0$のとき
$N≧_rN_t+_sN$
$M≦_sM$
$N$:設計用圧縮力
$_rN_t$:鉄筋コンクリート部分が引張力のみを受ける場合の許容引張力
$_rN_c$:鉄筋コンクリート部分が圧縮力のみを受ける場合の許容圧縮力
$_rN$:鉄筋コンクリート部分の許容圧縮力
$M$:設計用曲げモーメント
$_rM$:鉄筋コンクリート部分の許容曲げモーメント
$_sM_0$:鉄骨部分が曲げモーメントのみ受ける場合の許容曲げモーメント
$_sM$:鉄骨部分の許容曲げモーメント
$_sN_c,_sN_t,_sM_0,_sN,_sM$は下式により算定します。
$_sN_c = {_s}A \cdot {_s}f_c$ $_sN_t = {_s}A_e \cdot {_s}f_t$ $_sM_o = {_s}Z \cdot {_s}f_t$■ $_sN$が圧縮力の場合
$\frac{_sN}{_sA} + \frac{_sM}{_sZ} = {_s}f_c$
■ $_sN$が引張力の場合
$\frac{_sN}{_sA} + \frac{_sM}{_sZ} = {_s}f_t$
$_sA$:鉄骨部分の断面積
$_sA_e$:ボルト穴を控除した鉄骨部分の有効断面積(現在未考慮:sAe=sA)
$_sf_c$:鉄骨の許容圧縮応力度
$_sf_t$:鉄骨の許容引張応力度
$_sZ$:鉄骨の断面係数
1) 日本建築学会:鉄骨鉄筋コンクリート構造計算基準・同解説;P.11-14,86-97 1987.6
rNc,rNtは下式により算定します。
$_rN_c$ = min ( $_rN_{c1}$, $_rN_{c2}$)
$_rN_c$ $_1$ = $A_e \cdot f_c'$
$_rN_c$ $_2$ = $\frac{A_e \cdot {_m}f_c'}{n}$
$_rN_t = - {_m}A \cdot {_m}f_t$
$A_e$:コンクリートの等価断面積
$_mA$:柱の全主筋断面積
$_mf_c$:主筋の許容圧縮応力度
$n$:ヤング係数比
$f_c$’:柱の鉄筋コンクリート部分の算定に用いるコンクリート許容圧縮応力度
$f_c' = f_c \cdot (1-15 \cdot {_s}p_c)$
$f_c$:コンクリートの許容圧縮応力度
$_sp_c$:圧縮側鉄骨比(= $_sa_c/(b・D)$)
$_sa_c$:圧縮側鉄骨フランジの断面積
ここで、 $f_{c'}$算定用の圧縮側鉄骨フランジ断面積( $_sa_c$)のとり方の例を以下に示します。圧縮側鉄骨フランジとして、下図の太線で示す部分をとります。
$f_{c'}$算定用の圧縮側鉄骨フランジ断面積( $_sa_c$)のとり方
$_rN,_rM$は以下により求めます。
■コンクリートで決まる場合
$0 < x_{n1} \verb|≦| 1$のとき
$_rn$ = $\frac{_rN}{b \cdot D \cdot f_c'}$ = $\frac{x_n1}{2} + n \cdot _mp_t \cdot \left( 2- \frac{1}{x_n1} \right)$
$_rm = \frac{_rM}{b \cdot D^2 \cdot f_c'} = \frac{x_n1}{12} \cdot (3-2 \cdot x_n1) + \frac{n \cdot {_m}p_t}{2 \cdot x_n1} \cdot (1-2 \cdot _{r}d_t1)^2$$0 < x_{n1} \verb|≦| 1$のとき
$_rn = \frac{_rN}{b \cdot D \cdot f_c'} = (1+2 \cdot n \cdot {_m}p_t) \cdot \left( 1- \frac{1}{2 \cdot x_n1} \right)$ $_rm = \frac{_rM}{b \cdot D^2 \cdot f_c'} = \frac{1}{2 \cdot x_n1} \cdot \left( \frac{1}{6} + n \cdot {_m}p_t \cdot (1-2 \cdot _{r}d_t1)^2 \right)$■圧縮鉄筋で決まる場合
$\frac{_rN}{b \cdot D \cdot _mf_t} = \frac{x_n1}{ n \cdot (x_n1 - _rd_c1)} \cdot _rn$ $\frac{_rM}{b \cdot D^2 \cdot _mf_t} = \frac{x_n1}{ n \cdot (1-_rd_t1-x_n1)} \cdot _rm$■引張鉄筋で決まる場合
$0 < x_{n1} \verb|≦| 1$のとき
$\frac{_rN}{b \cdot D \cdot _mf_t} = \frac{x_n1}{ n \cdot (1-_rd_t1-x_n1)} \cdot _rn$ $\frac{_rM}{b \cdot D^2 \cdot _mf_t} = \frac{x_n1}{ n \cdot (1-_rd_t1-x_n1)} \cdot _rm$$x_{n1} < 0$のとき
$\frac{_rN}{b \cdot D \cdot _mf_t} = \frac{_mp_t \cdot (2 \cdot x_n1-1)}{1-_rd_t1-x_n1}$ $\frac{_rM}{b \cdot D^2 \cdot _mf_t} = \frac{_mp_t \cdot (1-2 \cdot _rd_t1)^2}{1-_rd_t1-x_n1}$$x_{n1}$:柱の鉄筋コンクリート部分の中立軸比(= $x_n/D$)
$x_n$:曲げ材の圧縮縁から中立軸までの距離
$_rd_t$ $_1$:rdtの全せいに対する比(= $_rd_t/D$)
$_rd_t$:引張縁から引張主筋重心までの距離
$_rd_c$ $_1$: $_rd_c$の全せいに対する比(= $_rd_c/D$)
$_rd_c$:圧縮縁から圧縮主筋重心までの距離
$r_n$:鉄筋コンクリート部分の許容軸方向力の無次元化量
$r_m$:鉄筋コンクリート部分の許容曲げモーメントの無次元化量
$n$:ヤング係数比
$_mp_t$:引張鉄筋比
$_mf_t$:主筋の許容引張応力度
$f_c'$:柱の鉄筋コンクリート部分の算定に用いるコンクリートの許容圧縮応力度
せん断力に対する検討
設計用せん断力が許容せん断力を下回ることを、次式により確認します。
$Q \verb|≦| Q_A$ (長期せん断力の検定)
$_sQ_D$ $\verb|≦|$ $_sQ _{AD}$ および $_rQ_D$ $\verb|≦|$ $_rQ _{AD}$ (短期せん断力の検定)
a) 許容せん断力【SRC規準】
鉄骨および鉄筋コンクリート部分の許容せん断力はSRC規準により算定します1)。長期許容せん断力( $_sQ_A$)は下式により求めます。
$Q_A$ = $(1+\beta) \cdot _rQ _{AL}$
$_rQ _{AL}$ = $b \cdot _rj \cdot a' \cdot f_s$
$a' = \left( \begin{array}{rr} _ra : \frac{b'}{b} \verb|≧| \frac{_ra}{3} \\ 3 \frac{b'}{b} : \frac{b'}{b} < \frac{_ra}{3} \\ \end{array} \right)$1) 日本建築学会:鉄骨鉄筋コンクリート構造計算規準・同解説;96-97, 1987.6
$b$:柱幅
$_rj$:鉄筋コンクリート部分の圧縮側と引張側の応力中心間距離(= $7/8・_rd$)
$f_s$:コンクリートの許容せん断応力度
$ r_α $ : せん断スパン比による割増係数
$_ra $ = $ \frac{4}{_rM/({_r}Q \cdot {_r}d)+1}$ かつ $1 \verb|≦| _{r}a \verb|≦| 2$
$_rM$:鉄筋コンクリート部分の設計用曲げモーメント
柱頭、柱脚の設計用曲げモーメントのうち大きい方とする。
$_rQ$:鉄筋コンクリート部分の設計用せん断力
柱頭、柱脚の設計用せん断力のうち大きい方とする。
$b'$:鉄骨フランジ位置でのコンクリート有効幅
β:鉄骨ウェブの形式と寸法による係数
$β = \left( \begin{array}{rr} \frac{n \cdot t_w \cdot {_s}d }{b \cdot {_r}j} \\ \frac{1.33n \cdot b_f \cdot t_f }{b \cdot {_r}j} \\ \end{array} \right)$
n:ヤング係数比
$t_w$:鉄骨のウェブ厚さ
$_sd$:鉄骨のフランジ重心間距離
$b_f$:鉄骨のフランジ幅
$t_f$:鉄骨のフランジ厚さ
鉄骨部分の短期許容せん断力は下式によります。
$_sQ_A = \left( \begin{array}{rr} d_w \cdot t_w \cdot {_s}f_s \\ \frac{4}{3} \cdot b_f \cdot t_f \cdot {_s}f_s \\ \end{array} \right)$$d_w$:鉄骨ウェブ長さ(=H-2t2)
$_sd$:鉄骨のフランジ重心間距離
$_sf_s$:鉄骨の許容せん断応力度
鉄筋コンクリート部分の短期許容せん断力は下式によります。
$_rQ _{AS}$ = min ( $_rQ _{A1}$, $_rQ _{A2}$)
$_rQ _{AS1}$ = $b \cdot _rj \cdot$ $(f_s+0.5 \cdot p_w \cdot _wf_t)$
$_rQ _{AS2}$ = $b \cdot {_r}j \cdot \left(2 \frac{b'}{b} \cdot f_s+p_w \cdot _wf_t \right)$
$p_w$: 帯筋比
$_wf_t$:主筋の許容圧縮応力度
b) 設計用せん断力
【構造規定】
SRC柱設計用せん断力決定方法を「構造規定」とした場合、鉄骨および鉄筋コンクリート部分の設計用せん断力は、構造規定により算定します2)。
■短期設計用せん断力
鉄骨部分の短期設計用せん断力( $_sQ_D$)、鉄筋コンクリート部分の短期設計用せん断力( $_rQ_D$)は次式により算定します。
$_sQ_D = \frac{_sZ}{_sZ+_ra_t \cdot _rj } \cdot Q_L+ \frac{_sM_1+_sM_2}{h'}$ (鉄骨部分)
$_rQ_D$= min ( $_rQ _{D1}$, $_rQ _{D2}$) (鉄筋コンクリート部分)
$_sQ _{D1}$ = $\frac{_ra_t \cdot _rj}{_sZ+_ra_t \cdot _rj }Q_L+ \cdot Q_L+ \frac{_sM_1+_sM_2}{h'}$
$_sQ _{D2}$ = $n \cdot (Q_L+Q_E-_sQ_D)$
$_sM_1$:鉄骨部分の一端の短期許容曲げモーメント(N・mm)
$_sM_2$:鉄骨部分の他端の短期許容曲げモーメント(N・mm)
h’:柱の内法高さ(mm)
$_rM_1$:鉄筋コンクリート部分の一端の終局曲げモーメント(N・mm)
$rM_2$:鉄筋コンクリート部分の他端の終局曲げモーメント(N・mm)
n:割増係数
積雪時、暴風時においては、短期設計用せん断力算定式の $Q_L$を $Q_L+Q_S$ $_n$、 $Q_L+Q_W$に置き換えて求めます。
【SRC規準】
SRC柱設計用せん断力決定方法を「SRC規準」とした場合、鉄骨部分および鉄筋コンクリート部分の設計用せん断力は以下により算定します2)。
■短期設計用せん断力
鉄骨部分の短期設計用せん断力( $_sQ_D$)、鉄筋コンクリート部分の短期設計用せん断力( $_rQ_D$)は次式により算定します。
$_sQ_D = \frac{_sM_d}{M_s } (Q_L+Q_E)$ (鉄骨部分)
ここで、 $_sM_d = {_s}M_o$、 $_rM_d = M_s-{_s}M_d$
2) 国土交通省:2007年版建築物の構造関係技術基準解説書;P.664-665,2007.8
鉄骨鉄筋コンクリート造 耐震壁の断面検定
記号説明
鉄筋コンクリート造 耐震壁に準じます。
加えて以下の記号を用います。
$_rf_s$ : コンクリートのせん断許容応力度
$_sf_s$ : 鉄骨のせん断許容応力度
$A_s$ : 鉄骨のせん断断面積
せん断力に対する検討
長期許容せん断力は $Q_1$、短期許容せん断力は $Q_1$ と $Q_2$ の大きい方とします。
$Q_w=p_s・t・l_e・_wf_t$ $Q_c=b・j・(1.5_rf_s+0.5_wf_t・p_w) + (_sf_s・A_s)$ $r=Min(r_1,r_2,r_3)$ $Q_D=Max(Q_E,Q_{DW})$ $Q_1=r・t・l・_rf_s$ $Q_2=r(Q_w+ΣQ_c)$ $Q_a=Max(Q_1,Q_2)$$Q_D$/ $Q_a$≦1.0
鉄骨鉄筋コンクリート造パネルゾーンの断面検定
鉄骨鉄筋コンクリート造接合部の検定は以下の式により行います。
※ 検討結果はCSV出力のみ対応しています。メニュー「ファイル」→「データ変換出力」→「CSV出力」→「断面検定情報/断面検定表/柱梁接合部/SRC」から出力できます。
長期荷重時:
$_cV・3f_s・(1+ \beta)$ ≧ $ \frac{h'}{h}(_BM_1 + _BM_2)$
短期荷重時:
$_cV・3f_s・(1+ \beta)$ ≧ $ \frac{h'}{h}(_BM_1 + _BM_2)$
ここで、各諸元は以下とします。
| cV | cVe | sV | β | |
|---|---|---|---|---|
| 梁SRC,RC | $_Cb \cdot _{mB}d \cdot _{mC}d$ | $\frac{_Cb+_Bb}{2} \cdot _{mB}d \cdot _{mC}d$ | $_Jt_w \cdot _{sB}d \cdot _{sC}d$ | $\frac{n \cdot _Jt_w \cdot _{sC}d}{_Cb \cdot _{mC}d}$ |
| 梁S | $_Cb \cdot _{sB}d \cdot _{mC}d$ | $\frac{_Cb}{2} \cdot _{sB}d \cdot _{mC}d$ |
| 接合部の形状 | jδ |
|---|---|
| 十字型 | 3 |
| ト字形、T字形 | 2 |
| L字形 | 1 |
$_cV$:柱梁接合部コンクリート部分の体積
$_cV_e$:柱梁接合部コンクリート部分の有効体積
$_sV$:柱梁接合部の鉄骨ウェブの体積
β:鉄骨ウェブ材の形式と寸法による係数
$C_b$:柱の幅
$B_b$:梁の幅
$_mB_d$:梁の上下の主筋間距離
$_mC_d$:柱の左右の主筋間距離
$_sB_d$:梁の鉄骨部分の上下弦材またはフランジの重心間距離
$_jt_w$:柱梁接合部の鉄骨のウェブの厚さ
$n$:ヤング係数比
接合部に集まる柱および梁における鉄骨部分と鉄筋コンクリート部分のそれぞれの曲げ耐力の和が、次式のいずれかを満たしている場合には、両部材間の鉄筋部分の応力伝達に対する安全性の検討を省略できます。
$0.4 \geq \frac{{_s}_CM_A}{{_s}_BM_A} \geq 2.5$ $0.4 \geq \frac{{_r}_CM_A}{{_r}_BM_A}$JFEシビル二重鋼管座屈補剛ブレースの断面検定
軸力に対する検討
短期許容軸力に対し、設計用軸力が下回っているか確認します。
座屈長さに対する検討
座屈長さが限界座屈長に対し、下回っているかを確認します。
座屈長さの計算方法は「2.3.4JFEシビル 二重鋼管座屈補剛ブレースの剛性」によります。
日鉄エンジニアリングアンボンドブレースの断面検定
軸力に対する検討
短期許容軸力に対し、設計用軸力が下回っているか確認します。
座屈長さに対する検討
座屈長さが限界座屈長に対し、下回っているかを確認します。
座屈長さは(L-2×L1)とします。
$L$:芯芯間長さ
$L1$:座屈長さ低減距離( L1 = ( L1(上) + L1(下) )/ 2 )
座屈長さが限界座屈長さを超えた場合は、鋼管サイズ(板厚、径)を上げるか、座屈長さを低減してください。
鉄骨の断面検定における断面性能
鉄骨部材の断面性能は、ユーザー設定により断面欠損を考慮して算定します注1)。組立品として寸法を直接入力した場合は、ロールHのr部分は無視して算定します。規格品の鋼材を選択した場合は、メーカーの公称値を採用します。
H形鋼材
断面係数(Z)
組立品(BH)として入力した場合の断面係数(Z)の算定は以下によります。なお、下式では断面欠損を考慮しておりません。また、組立品(BH)のS造柱部材において、フランジとウェブの材料強度が異なる場合は、ウェブの規準強度(F値)により置換して算定します。
■強軸側の断面係数
$Z = \frac{I}{H/2}$$Z$:強軸側の断面係数(cm3)
$I$:断面2次モーメント(cm4)
・曲げ設計でウェブを考慮しない場合
$I = I_f$・曲げ設計でウェブを考慮する場合
$I = I_f+I_w$ $I_f = \frac{B \cdot H^3-B \cdot (H-2 \cdot t_f)^3}{12}$ $I_w = \frac{t_w \cdot (H-2 \cdot t_f)^3}{12} \times (F_w/F_f)$$H$:鉄骨はりせい(cm)
$B$:フランジ幅(cm)
$t_w$:ウェブ厚(cm)
$t_f$:フランジ厚(cm)
$F_w$:ウェブの規準強度(N/mm2)
$F_f$:フランジの規準強度(N/mm2)
■弱軸側の断面係数
$Z = \frac{I}{B/2}$$Z$:弱軸側の断面係数(cm3)
$I$:断面2次モーメント(cm4)
$I = I_f+I_w$ $I_f = 2 \cdot \frac{t_f \cdot B^3}{12}$ $I_w = \frac{(H-2 \cdot t_f) \cdot {t_w}^3}{12} \times (F_w/F_f)$注1) メインメニュー「設計・計算条件」→「断面算定条件」→「S造」参照。
継手部の断面欠損の考慮
鉄骨造梁の断面性能において、ボルト穴による継手部の断面欠損を欠損率(%)としてフランジ・ウェブの各断面に対して評価します。
$I{_f}' = \frac{B \cdot H^3-B \cdot (H-2 \cdot t_f)^3}{12} \cdot (1-\beta_f/100)$ $I{_w}' = \frac{t_w \cdot (H-2 \cdot t_f)^3}{12} \cdot (1-\beta_f/100)$$I_{f'}$:継手部の欠損を考慮したフランジの断面2次モーメント
$β_f$:継手部のフランジの欠損率(%)
$I_{w'}$:継手部の欠損を考慮したウェブの断面2次モーメント
$β_w$:継手部のウェブの欠損率(%)
c) スカラップによる断面欠損の考慮
端部の断面性能において、スカラップによる欠損をウェブ断面に対する欠損率(%)として評価します。
$I{_w''} = \frac{t_w \cdot ( (H-2 \cdot t_f)(1-\alpha_w/100) ) ^3}{12}$$I_{w''}$:スカラップの欠損を考慮したウェブの断面2次モーメント
$α_w$:スカラップによる欠損率(%)
角形鋼管
断面係数(Z)
組立品として入力した場合、断面係数(Z)の断面係数の算定は以下によります。
$Z = \frac{I}{H/2}$ $I_f = \frac{B \cdot H^3-(B-2 \cdot t_1)(H-2 \cdot t_2)^3}{12}$せん断変形用断面積(AS)
$A_s = 2 \cdot t_1 \cdot (H-2 \cdot t_2)$※上図の着色部分がせん断変形用断面積にあたります。
鋼管
断面係数(Z)
$Z = \frac{I}{D/2}$ $I = \frac{\pi}{64} \cdot ( D^4-(D-2 \cdot t)^4 )$※上図の着色部分がせん断変形用断面積にあたります。
せん断変形用断面積( $A_S$)
鋼管のせん断変形用断面積( $A_S$)は全断面積の1/2とします。
$A_s = \frac{\pi \cdot t \cdot (D-t)}{2}$鉄骨ブレースの断面検定
記号説明
$A$ :全断面積
$f_t$ :許容引張応力度
$f_c$ :許容圧縮応力度
$σ_c$ :圧縮応力度
$N$ :設計用軸力
軸力に対する検討
$σ_c=N/A$ :圧縮応力度
$σ_c/f_c≦1.0$$σ_t=N/A$ :引張応力度
$σ_t/f_t≦1.0$05. 非線形モデル
05. 非線形モデルのサブセクション
各部材モデルの非線形特性
各部材モデルの非線形特性
各部材の非線形特性を部材、構造種別ごとに下表に示します。
| 部材 | 自由度 | RC造・SRC造・CFT造 | S造 |
|---|---|---|---|
| 梁 | 曲げ | トリリニア | バイリニア |
| 軸方向 | 弾性剛性* | 弾性剛性* | |
| せん断 | 弾性剛性* | 弾性剛性* | |
| 柱 | 曲げ | ファイバーモデル | ファイバーモデル |
| 軸方向 | ファイバーモデル | ファイバーモデル | |
| せん断 | 弾性剛性* | 弾性剛性* | |
| 耐震壁 | 曲げ | ファイバーモデル | ― |
| 軸方向 | ファイバーモデル | ― | |
| せん断 | トリリニア | ― | |
| ブレース | 曲げ | ― | ― |
| 軸方向 | ― | バイリニア | |
| せん断 | ― | ― |
* 指定により弾塑性考慮可能
梁
梁
梁部材は、同一階の2つの節点を端点として定義し、両端に剛塑性回転バネを有する線材としてモデル化します。モデルの仮定条件は以下のとおりです。
■曲げ剛性、せん断剛性(弾性)、軸剛性(弾性)を持ち、指定によりねじれ剛性を考慮することが可能です。
■鉄筋コンクリート、鉄骨鉄筋コンクリート造梁の場合は、曲げひび割れを考慮します。
■梁の断面性能は中央の断面形状から算定します。鉄筋コンクリート造、鉄骨鉄筋コンクリート造梁の場合は、スラブを含めたコンクリート形状と鉄筋あるいは鉄骨の影響を考慮します。
■梁の曲げ・せん断耐力は、端部の断面より求めます。曲げ耐力には、下図に示す部材の両端で計算した正負応力を採用し、せん断耐力は両端の正負応力状態について求めた絶対値の最小値を用います。
■せん断スパン( $M/Q$)およびモーメント反曲点長さ( $a$)は可撓長さ( $l_0$)の $1/2$とし、他端ピンの場合はせん断スパン( $M/Q$)が可撓長さ( $l_0$)に一致するものとします。
$a_i$, $a_j$:i端、j端のモーメント反曲点高さ( $ = 1/2 \cdot l_0 $)
$l_0$:内法スパン
共通
梁の曲げ非線形特性のモデル化
梁の曲げ非線形特性は、部材の両端に取付く剛塑性回転バネにより評価します。なお、塑性率の計算はバイリニアの場合は第1折れ点、トリリニアの場合は第2折れ点を起点とします。
部材の曲げ非線形特性( $M-θ$関係)は、曲げ降伏時剛性低下率( $α_y$)を用いて、トリリニア型のスケルトンカーブにモデル化します。
ここで、反曲点位置をaとしたとき、長さ2aとなるような逆対称モーメント分布を持つ仮想部材を考えます。
この部材の降伏変形角を $θ_y$とすると、せん断変形を考慮して下式で表されます。
$$\theta_y = \left( \frac{M_y \cdot a^2}{3 \cdot E \cdot I_e}+ \frac{M_y}{G \cdot A_s} \right) \cdot \frac{1}{a} \cdot \frac{1}{\alpha_y}$$この弾塑性の復元力特性から弾性変形分を差引いて、剛塑性回転バネの特性を求めます。降伏変形角(
$θ_y$)は、
曲げ降伏時変形角(yθe)と塑性変形角(yθp)の和により下式となります。
以上より、塑性変形(yθp)は下式となります。
$${_y}\theta_p = \left( \frac{1}{\alpha_y}-1 \right) \cdot \left( \frac{M_y \cdot a^2}{3 \cdot E \cdot I_e}+ \frac{M_y}{G \cdot A_s} \right) \cdot \frac{1}{a}$$したがって、曲げひび割れ後の材端回転バネのバネ定数( $_2 K_\theta$)は下式となります。
$$_2 K_\theta = \frac{M_y-M_c}{{_y}\theta_p}$$
$M_y$:曲げ降伏モーメント
$α_y$:曲げ降伏時剛性低下率
$a$:反曲点高さ
$E$:ヤング係数
$G$:せん断弾性係数
$I_e$:断面2次モーメント
$A_S$:せん断変形用断面積
鉄筋コンクリート造
鉄筋コンクリート造梁の曲げ復元力特性
鉄筋コンクリート造梁の曲げ復元力特性の諸元値を以下に示します。なお、耐震壁付梁の場合は弾性とします。
各耐力式に用いる主な記号は以下のとおりとします。
$y_i$ :梁下端からの各鉄筋重心までの距離
$a_i$:各鉄筋断面積
$i=1$ :下端1段筋
$i=2$ :下端2段筋
$i=3$ :上端1段筋
$i=4$:上端2段筋
$i=5$ :スラブ筋
$a_t$:引張鉄筋断面積
$a_s$:スラブ筋の断面積
$b$:T型梁の有効幅
$B$:梁幅
$D$:梁せい
$t$:スラブ厚
※ 鉄筋の剛性を考慮しない場合は、「剛性条件」→「RC造」で"各断面の剛性計算時,鉄筋の剛性を考慮しない"にチェックを入れる必要があります。
※ スラブ筋を考慮する場合は、「終局耐力条件」でスラブ筋の断面積を直接入力する必要があります。
※ スラブ筋の重心位置はスラブ厚(t)の1/2とします。
※ 初期設定では片持ち床のスラブ筋は考慮しません。考慮する場合は、「剛性計算条件」→「剛性条件1」で"協力幅の計算に片持ちスラブを含む"にチェックを入れる必要があります。
※ 片持ち床のスラブ筋を考慮した場合、曲げ終局強度を計算する際の圧縮縁から引張鉄筋重心までの距離はスラブ筋を考慮したうえで計算したものになります。
※ 引張鉄筋比( $p_t$)へのスラブ筋の考慮は以下のとおりとします。
■スラブ筋を考慮する場合
上端引張:
$p_t$ =
$(a_s + a_{t{上}})/(B \cdot D)$
下端引張:
$p_t$ =
$a_{t{下}}/(b \cdot D)$
■スラブ筋を考慮しない場合
上端引張:
$p_t$ =
$a_{t{上}}/(B \cdot D)$
下端引張:
$p_t$ =
$a_{t{下}}/(B \cdot D)$
・上端引張(スラブ引張)時は、梁幅Bと梁せいDからなる長方形梁を想定
・下端引張(スラブ圧縮)時は、T型梁の有効幅bと梁せいDからなる仮想の長方形梁を想定
※ 非線形解析においては、鉄筋およびコンクリートのヤング係数は下式によります1)。
$$E_c = 3.35 \cdot 10^4 \cdot \left( \frac{\gamma}{24} \right)^2 \cdot \left( \frac{F_c}{60} \right) ^\frac{1}{3}$$ $$E_s = 2.05 \cdot 10^5$$
$E_c$:コンクリートのヤング係数(N/mm2)
$γ$:コンクリートの気乾単位体積重量(kN/m3)
$F_c$:コンクリートの設計基準強度(N/mm2)
$E_s$:鉄筋のヤング係数(N/mm2)
1) 日本建築学会:鉄筋コンクリート構造計算基準・同解説;P.50-51,2010.2
(1) 曲げひび割れ強度( $M_c$)
鉄筋コンクリート造梁の曲げひび割れ強度(Mc)は構造規定(略算式)により計算します2)。
$$M_c = \kappa \cdot \sqrt{F_c} \cdot Z_e$$$κ$:ひび割れモーメント算定用係数(=0.56)
$Z_e$:鉄筋を考慮した断面係数(mm3)
上端引張の場合 $I_e/(D-g)$
下端引張の場合 $I_e/g$
$I_e$:断面2次モーメント(mm4)
異種強度梁の場合、引張側のコンクリート強度(上端引張の場合 $F_{cu}$, 下端引張の場合 $F_{cd}$)を用います。
2) 国土交通省:2007年版建築物の構造関係技術基準解説書;P.621-623,2007.8
(2) 曲げ降伏時剛性低下率( $α_y$)
鉄筋コンクリート造梁の曲げ降伏時剛性低下率( $α_y$)は下式で算定します2)。
$$ \alpha_y = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \left( 0.043+1.635 n \cdot p_t+0.043 \frac{a}{D} \right) \left( \frac{d}{D}\right)^2 & \displaystyle \left( 2.0 \leq \frac{a}{D} \leq 5.0\right) \\ \displaystyle \left(-0.0836+0.159 \frac{a}{D}\right) \left( \frac{d}{D}\right)^2 & \displaystyle \left( 1.0 \leq \frac{a}{D} < 2.0\right) \end{array} \right. \end{align}$$※ $ \frac{a}{D}<1.0$または $5.0 < \frac{a}{D}$の場合、 $\frac{a}{D}$はそれぞれ $1.0 , 5.0$とします。
$p_t$:引張鉄筋比(小数)
$a/D$:シアスパン比
$a$:せん断スパン(= $l_0/2$)(mm)
$l_0$:可撓長さ(mm)
$d$:有効せい(圧縮縁から引張鉄筋重心までの距離)(mm)
$n$:ヤング係数比(= $Es/Ec$)
・上端引張の場合
$p_t = \frac{\sum a_i}{B \cdot D} \quad d = \frac{\sum a_i \cdot y_i}{\sum a_i}$・下端引張の場合(指定によりb=Bとすることも可能です)
$p_t = \frac{\sum a_i}{b \cdot D} \quad d = \frac{\sum a_i \cdot (D-y_i)}{\sum a_i}$$a_i$:各鉄筋断面積(mm2)
$y_i$:梁下端からの各鉄筋重心位置(mm)
※ スラブ筋断面積が入力されている場合は、上端引張側の $p_t$にスラブ筋の断面積を含めて算定します。
※ T型梁または腰壁、垂壁付梁の場合は、求まった $α_y$を下式により補正します3)。指定により、補正しないこともできます。
・上端引張の場合
$α_y'=α_y \frac{I_{e0}+I_{wl}}{I_e+I_{wu}+I_{wl}}$※腰壁、垂壁が存在しない場合、 $α_y'=α_y \frac{I_{e0}}{I_e}$と等価
・下端引張の場合
$α_y'=α_y \frac{I_{e0}+I_{wl}}{I_e-I_{wu}+I_{wl}}$※腰壁、垂壁が存在しない場合、 $α_y'=α_y$と等価
$I_{e0}$:矩形断面の断面2次モーメント(mm4)
$I_e$:T型断面の断面2次モーメント(mm4)
$I_{wu}$:腰壁断面の断面2次モーメント(mm4)
$I_{wl}$:垂壁断面の断面2次モーメント(mm4)
異種強度梁の場合、ヤング係数比の算定において、引張側のコンクリート強度(上端引張の場合 $F_{cu}$, 下端引張の場合 $F_{cd}$)を用います。
3) 梅村魁;鉄筋コンクリート建物の動的耐震設計法;技報堂;P.106-108,1973.8
(3) 曲げ終局強度( $M_u$)
a) 大梁の曲げ終局強度
鉄筋コンクリート造梁の曲げ終局強度( $M_u$)は構造規定による略算式もしくはACI規準に基づく平面保持仮定により算定します4)。
略算式
$$M_u = 0.9 \cdot (\sum \sigma_{yi} \cdot a_i) \cdot d$$ $$ d = \frac{\sum \sigma_{yi} \cdot a_i \cdot d_i}{\sum \sigma_{yi} \cdot a_i} $$$σ_{yi}$:各引張鉄筋の降伏強度(N/mm2)
$a_i$:各引張鉄筋の断面積(mm2)
$d$:梁有効せい(圧縮縁から引張鉄筋重心位置までの距離)(mm)
$d_i$:圧縮縁から各引張鉄筋重心位置までの距離(mm)
4) 国土交通省:2007年版建築物の構造関係技術基準解説書;P.623,2007.8
平面保持
「鉄筋コンクリート造柱の終局耐力」をご確認ください。
b) 腰(垂)壁付き大梁の曲げ終局強度
腰(垂)壁付き鉄筋コンクリート造梁の曲げ終局強度( $M_u$)は構造規定により算定します4)。
$$M_u=a_{te} \cdot σ_y \cdot (d_e-0.5x_n)$$ただし、 $a_{te}=a_t+Σa_{t'}\left(\frac{σ_{y'}}{σ_y}\right)$ かつ $a_{te}\le(0.85F_c \cdot t \cdot x_{nb}/σ_y)-Σa_{t'}\left(\frac{σ_{}y'}{σ_y}\right)$
$x_n=a_{te} \cdot σ_{y}/(0.85F_c \cdot t)$
$F_c$:コンクリート圧縮強度
$t$:圧縮側の壁厚(壁がない場合、 $t=b$)
$_cε_B$:コンクリートの圧縮強度歪み( $0.002$)
$_sε_y$:梁主筋降伏点時の歪み( $σ_y/_sE$)
c) 異種強度梁の曲げ終局強度
略算式
異種強度梁特有の変更はありません。
平面保持
終局曲げ耐力の算定における留意点は以下となります。
- $F_c$を圧縮側のコンクリート強度(上端引張の場合 $F_{cd}$, 下端引張の場合 $F_{cu}$)と置き換えて既存の式で算定します。
- 計算条件>部材復元力特性計算条件>終局耐力条件2>平面保持スラブの設定の片側スラブ幅の値を採用します。
- 中立軸位置と水平接合面位置が異なる場合でも、中立軸位置より上は $F_{cu}$, 中立軸位置より下は $F_{cu}$とします(下図参照)。
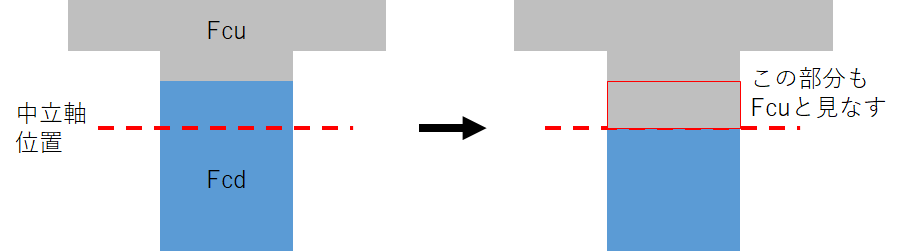
平面保持を選択した場合の終局曲げ耐力の算定における留意点
鉄筋コンクリート造梁のせん断復元力特性
せん断復元力特性は指定により考慮できます。鉄筋コンクリート造梁のせん断復元力特性の諸元値を以下に示します。なお、壁付梁の場合は指定によらず弾性とします。
せん断終局耐力は上端引張、下端引張の耐力の平均値を採用します。
(1) 大梁のせん断終局強度(RC)
RC大梁のせん断終局強度は下記に式により計算されます。スラブについては $b_e≦1.2b$ の範囲で考慮されます。
$$Q_{su} = \left( \frac{k \cdot p_t^{0.23} (18+F_c)}{ \displaystyle \frac{M}{(Q \cdot d)}+0.12}+0.85 \sqrt{p_w \cdot \sigma_{wy}} \right) \cdot b_e \cdot j_e$$ $\kappa : 0.053 または 0.068$$p_{te}$ : $a_t/(b・d)$
$d$ : 大梁の引張鉄筋の中心から圧縮縁までの距離
$p_w・σ_wy$ : 大梁の帯筋比とその降伏強度の積
$σ_0$ : $N/(b・j)$
$j : 7d/8$$M/Q・d$ : せん断スパン比 ( $1.0≦M/Q・d≦3.0$)
| $κ$ | $σ_{wy}$ | |
|---|---|---|
| ウルボン1275 | $0.053$ | 特になし |
| パワーリング785 | $0.053$ | $σ_{wy}=25・Fc (Fc<32)$ |
| パワーリング685 | $0.068$ | 特になし |
| エムケーフープ | $0.053$ | $σ_{wy}=25・Fc (Fc < 31.4)$ |
(2) 腰(垂)壁付き大梁のせん断終局強度(RC)
腰(垂)壁付きRC大梁のせん断終局強度は下記に式により計算されます。
$$Q_{su} = \left( \frac{k \cdot p_t^{0.23} (18+F_c)}{\displaystyle \frac{M}{(Q \cdot d)}+0.12}+0.85 \sqrt{p_we \cdot \sigma_{wy}} \right) \cdot b_e \cdot j_e$$$k$: $0.053$ または $0.068$
$p_{te}:a_{t}/(b_{e} \cdot d_{e})$$d_{e}$ : 大梁の引張鉄筋の中心から圧縮側壁の最外縁までの距離
$p_{we} \cdot \sigma_{wy}$ : $p_w \cdot \sigma_{wy}(b/b_e)+p{_sh} \cdot \sigma_{sy}(t/b_e)$
$p_{w} \cdot \sigma_{wy}$ : 大梁の帯筋比とその降伏強度の積
$p_{sh} \cdot \sigma_{sy}$ : 腰(垂)壁の横筋比とその降伏強度の積
$\sigma_{0e}$ : $N/(b_e \cdot j_e)$
$j_{e}$ : $7d_{e}/8$
$b_{e} = \Sigma A/L'$ : 断面積とせいを同じにしたときの等価幅
$M/Q \cdot d_{e} = \frac{h_{CW0}}{L'} \quad (0.5 \leq M/Q \cdot d \leq 2.0)$$h_{CW0}$:反曲点の高さ
$L'$:腰(垂)壁を含む全せい
高強度せん断補強筋を用いた場合は以下が適用されます。
| $κ$ | $σ_{wy}$ | |
|---|---|---|
| ウルボン1275 | $0.053$ | 特になし |
| パワーリング785 | $0.053$ | $σ_{wy}=25・Fc (Fc<32)$: |
| パワーリング685 | $0.068$ | 特になし |
| エムケーフープ | $0.053$ | $σ_{wy}=25・Fc (Fc< 31.4)$ |
(3) 大梁のせん断ひび割れ強度(RC)
指定により、ひび割れを考慮したトリリニアとしてモデル化します。ひび割れ耐力は以下のように計算します。せん断降伏時歪みは1/250としてトリリニアモデルを作成します。
$$Q_c = \left( \frac{0.061 \cdot (Fc+49)}{\left( \frac{M}{Q \cdot d} \right)+1.7} \right) \cdot b \cdot j$$
鉄筋コンクリート造梁の軸復元力特性
指定により、軸復元力特性を考慮する場合には以下の式により復元力特性を設定します。
(1) 引張ひび割れ軸力
$$N_{ct} = \kappa \sqrt{F_c} \cdot A_c$$$κ$:ひび割れ軸力算定用係数(=0.56)
$Ac$:コンクリート断面積(mm2)
$Fc$:コンクリート強度(N/ mm2)
(2) 引張降伏軸力
$$N_{ut} = at \cdot \sigma_y$$$a_t$:鉄筋断面積(mm2)
$σ_y$:鉄筋材料強度(N/mm2)
(3) 圧縮降伏軸力
$$N_{uc} = at \cdot \sigma_y+F_c \cdot (A_c-at)$$鉄骨造
鉄骨梁の曲げ復元力特性
指定により、曲げ復元力特性を考慮する場合には以下の式により復元力特性を設定します。
(1) 全塑性モーメント $M_p$
$$M_p=Z_p・σ_y$$$Z_p$:塑性断面係数(mm3)
$σ_y$:鉄骨降伏強度(N/mm2)
(2) 横座屈モーメント $M_{cr}$
横座屈を考慮する場合、鋼構造塑性設計指針に基づき以下の式により計算します。鉄骨材料はフランジ部の材料を採用し、横座屈を考慮する断面形状はH形鋼のみとします。
a) SN400, SS400,SM400材( $σ_y$=235N/mm2)
$$ \frac{M_{cγ}}{M_P} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle 1.0 & \left( 0 \leq \frac{l_b・H}{A_f} \leq 300 \right) \\ \displaystyle 1-0.00075 \cdot \left( \tfrac{l_b・H }{A_f}-300\right) & \left( 300 < \frac{l_b・H}{A_f} \leq 835 \right)\\ \displaystyle \frac{500}{\frac{l_b \cdot H}{A_f}} & \left( 835 < \frac{l_b・H}{A_f} \right) \end{array} \right. \end{align}$$b) SN490, SM490, SM490T材( $σ_y$=325N/mm2)
$$ \frac{M_{cγ}}{M_P} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle 1.0 & \left( 0 \leq \frac{l_b・H}{A_f} \leq 220 \right) \\ \displaystyle 1-0.0010 \cdot \left( \tfrac{l_b・H }{A_f}-220 \right) & \left( 220 < \frac{l_b・H}{A_f} \leq 605 \right)\\ \displaystyle \frac{363}{\frac{l_b \cdot H}{A_f}} & \left( 605 < \frac{l_b・H}{A_f} \right) \end{array} \right. \end{align}$$c) その他
$$ \frac{M_{cγ}}{M_P} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle 1.0 & \left( 0 \leq \frac{l_b・H}{A_f} \leq \frac{70500}{α} \right) \\ \displaystyle 1- \frac{0.4}{ \frac{117000}{0.6σ_y} - \frac{70500}{σ_y}} \cdot \left( \tfrac{l_b・H}{A_f}- \tfrac{70500}{σ_y} \right) & \left( \frac{70500}{α} < \frac{l_b・H}{A_f} \leq \frac{117000}{0.6σ_y} \right)\\ \displaystyle \frac{ \frac{117000}{σ_y}}{{l_b}{A_f}} & \left( \frac{117000}{0.6σ_y} < \frac{l_b・H}{A_f} \right) \end{array} \right. \end{align}$$$l_b$:横方向補剛材の間隔(mm)
$H$:梁のせい(mm)
$A_f$:圧縮フランジの断面積(mm2)
鉄骨梁の軸復元力特性
指定により、軸復元力特性を考慮する場合には以下の式により復元力特性を設定します。
(1) 引張降伏軸力・圧縮降伏軸力
$$N_u = A_f \cdot \sigma_{fy}+A_w \cdot \sigma_{wy}$$$A_f$:フランジ断面積(mm2)
$A_w$:ウェブ断面積(mm2)
$σ_{fy}$:鉄筋材料強度(N/mm2)
$σ_{wy}$:鉄骨材料強度(N/mm2)
鉄骨鉄筋コンクリート造
鉄骨鉄筋コンクリート造梁の曲げ復元力特性
鉄骨鉄筋コンクリート造梁の曲げ復元力特性は、RC部分をトリリニア、S部分をバイリニアとして累加し、エネルギー吸収能力において等価なトリリニア型スケルトンカーブを求めます。
鉄骨鉄筋コンクリート造梁のせん断復元力特性
(1) 大梁のせん断終局強度(SRC)
SRC大梁のせん断終局強度は下記の3式からの選択により計算されます。
a) SRC規準
$$Q_u = ({_r}Q_u+{_s}Q_u)$$ $$_rQ_u= min(_rQ_{u1}, _rQ_{u2})$$ $$_sQ_u= min(_sQ_{u1},_sQ_{u2})$$ $$_rQ_{u1}=b \cdot {_r}j(0.5 \times \alpha \cdot f_s+0.5 \cdot {_r}p_w \cdot _{rw}\sigma_y)$$ $$_rQ_{u2}=b \cdot {_r}j(b'/bf_s+{_r}p_w \cdot _{rw}\sigma_y)$$ $$_{s}Q_{u1}={_s}A_w \cdot {_s}\sigma_y/ \sqrt{3}$$ $$_{s}Q_{u2}=\Sigma{_s}M_u/l'$$ $$f_s = \min (0.15 \times Fc,22.5+ \frac{4.5 \times Fc}{100})$$ $$ a = 4/ (M/(Q \cdot rd)+1 ) かつ 1 \leq a \leq 2 $$$b$:梁幅
$b'$:鉄筋フランジ位置のコンクリート有効幅
$_rj$:鉄筋コンクリート部分の応力中心間距離
$_rd$:梁の有効せい
$_rp_w$:せん断補強筋比
$_{rw}\sigma_y$:せん断補強筋の材料強度
$_sA_w$:せん断力が作用する方向の鉄骨ウェブ断面積
$_s\sigma_y$:鉄骨ウェブの材料強度
$F_c$:コンクリートの設計基準強度
$_sM_u$:鉄骨部分の一端あるいは他端における全塑性モーメント
$l'$:内法スパン
b) SRC診断式
スラブについては $b_e≦1.2b$の範囲で考慮されています。
$$Q_{su} = \left( \frac{k \cdot p_t^{0.23} \cdot k_{cs}(18+F_c)}{M/(Q \cdot d)+0.12}+0.85 \sqrt{p_w \cdot \sigma_{wy}} \right) \cdot b_e \cdot j_e+{_s}Q_u$$ $$ _sQ_u = min \displaystyle \left( \frac{2 \cdot _sM_0}{h_0} , t_w \cdot h_w \cdot _s \sigma_{wy} \sqrt{3} \right)$$$k$: $0.053$または $0.068$
$p_{w}:a_{t}/(b \cdot d)$$k_{cs}:(0.5+b`/b)$かつ1.0以下
$d$:大梁の引張鉄筋の中心から圧縮縁までの距離
$p_{w} \cdot \sigma_{wy}$:大梁の帯筋比とその降伏強度の積
$\sigma_{0}:N/(b \cdot j)$$j$: $7d/8$
$M/Q \cdot d$:せん断スパン比 $(1.0≤M/Q \cdot d≤3.0)$
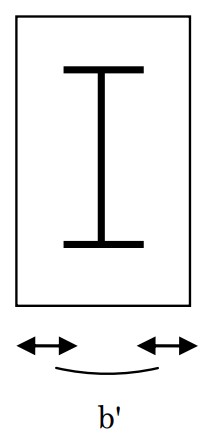
c) 構造関係技術基準解説書
$$Q_u = (_{r}Q_u+{_s}Q_u)$$ $$_rQ_u= min(_rQ_{u1}, _rQ_{u2})$$ $$_sQ_u=min(_sQ_{u1}, _sQ_{u2})$$ $$_rQ_{u1}=b \cdot _rj ( \alpha \cdot f_s+0.5 \cdot_rp_w \cdot _{rw} \sigma_y)$$ $$_rQ_{u2}= b \cdot _rj ( 2b'/bf_s+_rp_w \cdot _{rw} \sigma_y)$$ $$_sQ_{u1} = _sA_w \cdot _s\sigma _y/\sqrt{3}$$ $$_sQ_{u2} = \Sigma _sM_u/l'$$ $$f_s = \min ( Fc/20,(5+Fc/100) \cdot 1.5 )$$ $$α = 4/ (M/(Q \cdot rd)+1 )$$
$b$:梁幅
$b'$:鉄骨フランジ位置のコンクリート有効幅
$_{r}j$:鉄骨コンクリート部分の応力中心間距離
$_{r}d$:梁の有効せい
$_rP_w$:せん断補強筋比
$_{rw}\sigma_y$:せん断補強筋の材料強度
$_rA_w$:せん断力が作用する方向の鉄骨ウェブ断面積
$_s\sigma_y$:鉄骨ウェブの材料強度
$F_{c}$:コンクリートの設計基準強度
$_sM_u$:鉄骨部分の一端あるいは他端における全塑性モーメント
$l'$:内法スパン
(2) 大梁のせん断終局強度(非充腹SRC)
a) 格子材
非充腹SRC(格子材)のせん断耐力式は以下によります。
$$Q_{su} = \left( \frac{k \cdot p_t^{0.23} \cdot k_{cs}(18+F_c)}{M/(Q \cdot d)+0.12}+0.85 \sqrt{{_r}p_w \cdot {_r}\sigma_{wy}+ \frac{1}{2}{_s}p_w \cdot {_s}\sigma_{wy}} \right) \cdot b_e \cdot j$$$κ$: $0.053$または $0.068$
$b$:梁の断面幅
$be$:梁の有効幅で以下の式による
$be=ΣAg/D$$Ag$:スラブの断面積を加算した梁の全断面積
$d$:梁の有効せい
$j$:応力中心間距離( $=0.8D$)
$p_t$:引張鋼材比( $_rp_t+_sp_t$)(%)
$_rp_t$:引張鉄筋比(%)
$_sp_t$:引張鉄骨比(%)
$_rp_w$:せん断補強筋比(= ${_r}a_w/(b\cdot {_r}s)$)
$_sp_w$:帯板比(= $_sa_w/(b・_ss)$)
$_ra_w$:1組のせん断補強筋断面積
$_sa_w$:1組の帯板の断面積
$_rs$, $_ss$:それぞれせん断補強筋および帯板の間隔
$_rσ_{wy}$, $_sσ_{wy}$:それぞれせん断補強筋および帯板の降伏点強度
$M/Q$:せん断スパン、弾性水平荷重解析結果より計算
$M/Q・d$:せん断スパン比( $1.0≦M/Q・d ≦3.0$)
b) ラチス材
非充腹SRC(ラチス材)のせん断耐力式は以下によります。
$$Q_{su} = \left( \frac{k \cdot {_r}p_t^{0.23} \cdot k_{cs}(18+F_c)}{M/(Q \cdot d)+0.12}+0.85 \sqrt{{_r}p_w \cdot {_r}\sigma_{wy}} \right) \cdot b_e \cdot {_r}j+{_s}Q_u$$ $${_s}Q_u=min\left(\frac{2\cdot{_s}M_0}{h_0}, {_D}A_s\cdot \sigma _y \cdot sin\theta\right) $$
$κ$ : $0.053$または $0.068$
$b$ :梁の断面幅
$be$ :梁の有効幅で以下の式による
$be=ΣAg/D$$Ag$ :スラブの断面積を加算した梁の全断面積
$d$ :梁の有効せい
$j$ :応力中心間距離( $=0.8D$)
$p_t$ :引張鋼材比( $_rp_t+_sp_t$)(%)
$_rp_t$ :引張鉄筋比(%)
$_sp_t$ :引張鉄骨比(%)
$_rp_w$ :せん断補強筋比(= $_ra_w/(b・_rs$))
$_sp_w$ :帯板比(= $_sa_w/(b・_ss$))
$_ra_w$ :1組のせん断補強筋断面積
$_sa_w$ :1組の帯板の断面積
$_rs$, $_ss$ :それぞれせん断補強筋および帯板の間隔
$ _rσ _{wy} $ , $ _sσ _{wy} $ :それぞれせん断補強筋および帯板の降伏点強度
$M/Q$ :せん断スパン、弾性水平荷重解析結果より計算
$M/Q・d$ :せん断スパン比( $1.0≦M/Q・d ≦3.0$)
$h_o$ :内法長さ
${_D}A$ :ラチス材の断面積
$θ$ :ラチス材と材軸のなす角
(3) 腰(垂)壁付き大梁のせん断終局強度(SRC)
腰(垂)壁付きSRC大梁のせん断終局強度は下記に式により計算されます。
$$Q_{su} = \left( \frac{k \cdot p_t^{0.23} \cdot k_{cs}(18+F_c)}{M/(Q \cdot d)+0.12}+0.85 \sqrt{p_{we} \cdot \sigma_{wy}} \right) \cdot b_e \cdot j_e$$
$k$ :
$0.053$または
$0.068$
$k_cs$ :梁材の鉄骨フランジ側面のせん断破壊による低減係数
$0.5+b'/b$ で1以下の値
$p_{te}$ :
$a_t/(b_e\cdot d_e)$
$d_e$ :大梁の引張鉄筋の中心から圧縮側壁の最外縁までの距離
$p_{we}\cdot \sigma_{wy}$ :
$p_w\cdot \sigma_{wy}(b/b_e)+p_{sh}\cdot\sigma_{sy}(t/b_e)$
$p_w\cdot \sigma_{wy}$ :大梁の帯筋比とその降伏強度の積
$p_sh{sh}\cdot \sigma_{sy}$ :腰(垂)壁の横筋比とその降伏強度の積
$p_{te}$ :
$N/(b_e\cdot j_e)$
$p_{te}$ :
$7d_e/8$
$b_e=\Sigma A/L'$
$M/Q\cdot d_e = \frac{h_{cw0}}{L'}$
$h_{cw0}$ : 半曲点高さ
$L'$ : 腰(垂)壁を含む全せい

鉄骨鉄筋コンクリート造梁の軸復元力特性
指定により、軸復元力特性を考慮する場合には以下の式により復元力特性を設定します。
(1) 引張ひび割れ軸力
$$N_{ct} = \kappa \sqrt{F_c} \cdot A_c$$$κ$:ひび割れ軸力算定用係数(=0.56)
$Ac$:コンクリート断面積(mm2)
$Fc$:コンクリート強度(N/ mm2)
(2) 引張降伏軸力
$$N_{ut} = at \cdot \sigma_{yr}+A_{st} \cdot \sigma_{ys}$$$at$:鉄筋断面積(mm2)
$σ_{yr}$:鉄筋材料強度(N/mm2)
$σ_{ys}$:鉄骨材料強度(N/mm2)
(3) 圧縮降伏軸力
$$N_{uc} = at \cdot \sigma_{yr}+A_{st} \cdot \sigma_{ys}+F_c \cdot (A_c-A_{st}-at)$$柱
柱
ファイバーモデル
柱部材は両端ファイバー梁要素にモデル化します。モデルの仮定条件を以下に示します。
■部材は複数の微小断面(以降、セグメントと称します)の集合とし、平面保持の仮定が成立するものとします。
■各セグメントは一軸の構成則(応力-ひずみ関係)を持ち、セグメント間に相互作用はないものとします。
■せん断剛性は通常の部材要素と同様に決定し、モーメント・軸力との相関は考慮しません。
■部材フェイスを危険断面位置(塑性ヒンジ発生位置)として応力を評価します。
■指定により弾性解析を行うことが可能です注1)。
ファイバーモデル計算方法(軸、曲げ)
断面内のひずみは軸方向ひずみ、y軸周り曲率、z軸周り曲率の3次元(3成分)で表されます。説明を簡略化するために、2次元(2成分)で図示すると下図のようになります。各セグメント位置でのひずみは、平面保持の仮定に従って軸ひずみ(ε)と曲率(φ)から求められます。
$N$:危険断面位置の軸力
$M$:危険断面位置の曲げモーメント
$ε$:軸ひずみ
$φ$:曲率
$ε_s$:鉄筋ひずみ
$ε_c$:コンクリートひずみ
各セグメント位置のひずみが決定されれば、上図のように各セグメントの構成則からひずみに対応するヤング係数が求められます。各セグメントのヤング係数と断面積を、下式のように積分して断面性能を求めます。
$EA$:断面全体に関するヤング係数×断面積
$ES$:断面全体に関するヤング係数×断面1次モーメント
$EI$:断面全体に関するヤング係数×断面2次モーメント
$_sE$:各セグメントのヤング係数
$_sA$:各セグメントの断面積
$_sL$:各セグメントの断面内原点位置(図心)からの距離
上式によって求めた危険断面位置での断面性能を用いて、部材全体の剛性を求めます。
部材は、塑性化領域の指定をしない場合は軸方向に2つのファイバー領域に分割、塑性化領域の指定をした場合は中央に弾性要素を含んだ3つのファイバー領域に分割してモデル化します。両端の非線形のファイバー領域では、危険断面位置で求めた断面性能が均等に分布すると仮定します。各ファイバーの領域中の剛性は一定とし、材全体の剛性は各領域の剛性が直列に連結したものとして求めます。
両端の塑性化領域の1領域分の剛性マトリクスを下式のように作成します。説明の簡略化のため、2次元要素としてのマトリクスを示します。<>括弧は、領域端回転角と軸力の相関性を表す項を示しています。
$_xF$:軸力
$_zF$:せん断力
$_yM$:曲げモーメント
$l$:部材長
$_xδ$:軸方向変位
$_zδ$:せん断方向変位
$_yθ$:回転角
上記のマトリクスを2領域分求め、弾性領域がある場合はさらに弾性領域を結合した要素内全体剛性マトリクスから、うち点2点に関する自由度を方程式から消去(マトリクスの縮約)し、両端変形を未知数とする梁要素としての剛性マトリクスを求めます。この後、通常の梁要素と同様に剛域変換・材端ばね変換を行い、最終的な要素剛性とします。各ファイバー断面の例を以下に示します。
ファイバー断面の設定
ファイバー断面における分割数は、以下のように設定されます。
RC断面
歪が大きくなる縁に対して分割を細かくする対数分割により、9分割します。
対数分割は以下のようなロジックとなります。
* 基準となる位置から、log(2), log(3), log(4), … と対数の引数を+1ずつした距離離れた位置を分割位置とする。
* 基準となる位置は、偶数分割の場合は断面中心(座標0)、奇数分割の場合は断面中心 ± log(2) / 2 が基準となる。
【偶数分割の場合】
断面分割位置は、0, log(2), log(3), log(4), …
【奇数分割の場合】
+方向の断面分割位置は、- log(2) / 2, - log(2) / 2 + log(3), -log(2) / 2 + log(4), …
-方向の断面分割位置は、 log(2) / 2, log(2) / 2 - log(3), log(2) / 2 - log(4), … 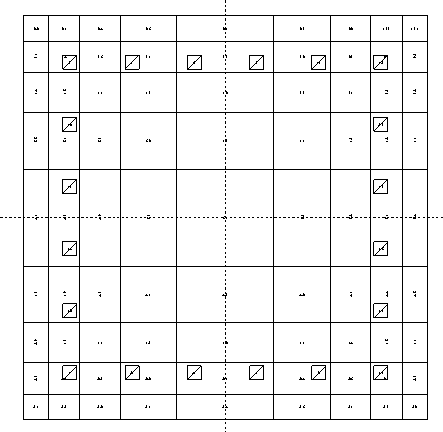
矩形断面
円形断面
鉄骨断面
パイプ型は等分割で16分割します。パイプ型以外は等分割で7分割します。
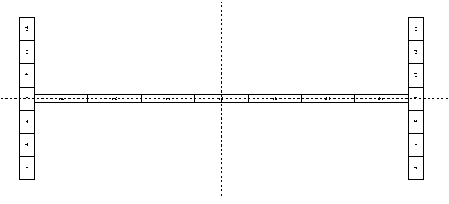
H型断面
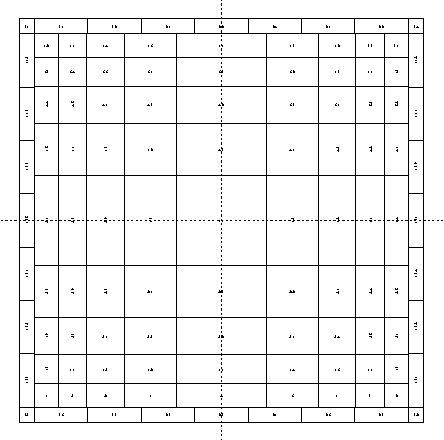
CFT 角型断面
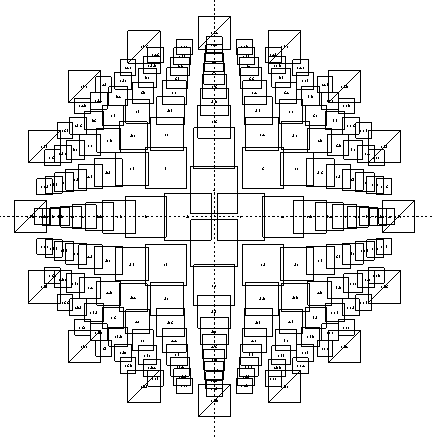
CFT 円形断面
分割要素の復元力特性については、鉄筋および鉄骨はバイリニアモデル、コンクリートはNewRcモデルとして評価します(ただし、NewRCの適用範囲であるFc60を超える強度、もしくはユーザー定義コンクリートの場合はBilinearの骨格曲線に対となります。適用範囲外のため、関数の形状が異常となるためです)。非充腹SRC柱については鉄骨弦材を分割断面としてモデル化し、ウェブ材はモデル化しません。第1折点においては、鉄筋および鉄骨の場合は圧縮・引張側ともに材料強度を1.1倍して断面積を乗じた値、コンクリートの場合は圧縮側で設計基準強度(Fc)に断面積を乗じた値を採用します。また、剛性低下率(α)はいずれも1/1000とします。
コンクリートの応力-ひずみ関係にはNewRCモデルを用います。
なお、コンクリート強度の計算にはコンファインド効果は考慮せず、以下の計算によりAおよびDを求めます。以下の数式において、応力度、ヤング係数の単位系は
$kg/cm^2$ を用いています。
コンクリートの応力-ひずみ関係 :
$
\frac{σ_c}{_ cσ _{cB}} = \frac{AX+(D-1)X^2}{1+(A-2)X+DX^2}
$
$_c \sigma _{cB}= \sigma _p$
$ \sigma _p = 1.0 _c \sigma _B$
$X = \frac{ε_c}{ε_c0} 、 A = \frac{E_cε{co}}{_ cσ _{cB}} 、 K = \frac{_ cσ _{cB}}{σ_p}$
$ \epsilon _{co} = \epsilon _o$$ \epsilon _o = 0.5243(_c \sigma _B)^{1/4} × 10^{-3}$
$E_c = 4k(_c \sigma _B/1000)^{1/3} × 10^5 × (γ/2.4)^2$$ k = 1.0$
$D = α + β_cσ_B$$α = 1.50$
$β = 1.68 × 10^{-3}$
$σ_c,ε_c$:コンクリートの軸方向応力およびひずみ
$_cσ_B$:コンクリートのシリンダー強度
$σ_p$:プレーンコンクリートの強度
$ _cσ _{cB}$:コンファインドコンクリートの強度(= $_cσ_B$)
$ε_{co}$:コンファインドコンクリートの強度時のひずみ
静的解析時には各分割断面の履歴は逆行型とし、動的解析時には鋼材は標準型、コンクリートは原点指向型としてモデル化します。
M-N相関耐力曲線を以下に例示します。本例は下図のファイバーモデルの断面解析結果を図化したもので、引張側を正、圧縮側を負として表示しています。
ファイバーモデルの塑性率について
本プログラムでは、塑性率の計算方法を以下の3つから選択できます。
(1) 塑性率基点歪みにより計算する方法
本手法ではセグメント(分割断面)の最大ひずみが塑性率基点ひずみを超えた時点を部材としての塑性率基点と見なします。いずれかのセグメントのひずみが塑性率基点ひずみを超えた時点の曲率を、断面全体の塑性率基点曲率として設定します。塑性率基点ひずみのデフォルト値は、RC部材の場合では引張0.01、圧縮0.005、鉄骨部材の場合では引張・圧縮ともに0.01としています。また、図心位置(初期剛性において、1点を加力した場合に断面に曲率が発生せず、軸ひずみのみが発生する点)に軸力が作用するものとして計算します。
塑性率は、最大応答曲率/塑性率基点曲率で計算されます。 この計算方法の場合、曲げ塑性率と軸塑性率は同じ値になります。 また、塑性率が1を下回る場合は評価されません。
この方法は、十分大きな縁歪みを設定することで、塑性率基点1の時点を最大耐力として定義したい場合に有用です。
一方、塑性化を許容し、塑性率をクライテリアとして評価する場合には、一律の縁歪みであらゆる軸力状態の降伏点を共通に設定することは難しいため不向きです。その場合は、(2)または(3)を選択するほうが適切です。
(2) 重み付け平均塑性率による計算方法
ファイバー断面における各分割断面の塑性率に対し、モーメントに対する寄与率によって重み付した値を用いて塑性率基点を設定します。下式によるJmが1.0以上となった時点の回転角を塑性率基点として塑性率を計算します。
この方法では、中立軸から遠い断面ほど歪が増加したときの全体のモーメント上昇に与える寄与が大きいことから、寄与が大きい断面の多くが塑性化する状況に至ったタイミングを部材が塑性化したタイミングとみなす、ということを意図しています。 本計算法法では、二軸曲げであったとしても縁のある一定領域が塑性化したタイミングが塑性率基点になり説明性の高い評価方法となること、曲げ塑性率と軸塑性率が別々の値として算出されることが利点として挙げられます。
曲げ剛性に与える寄与により重みづけしていることで、あらゆる軸力状態で顕著に剛性低下が生じた時点が塑性率基点となることから、1より大きな塑性率をクライテリアとする場合に向いています。
また、この方法の場合、塑性率基点となるステップの曲率に対する最大応答曲率を用いるか、塑性率基点たわみ角に対する最大応答たわみ角を用いるか選択することが可能です。
一般に、曲率は変位の2階微分、たわみ角は変位の1階微分のような関係になるため、曲率のほうが局所的に大きな応答が生じやすく、塑性率が大きくなりやすい傾向にあります。一方たわみ角は、層間変形角と比較的近いオーダーとなるため、曲率に比べて極端な塑性率が発生しにくくなります。
$J_m$:曲げ塑性率基点評価式
$A$:分割断面断面積
$x$:分割断面断面内座標
$x_n$:中立軸位置
$σ_y$:分割断面降伏応力度
$ε_x,ε_y$:分割断面歪み
$μ$:分割断面の塑性率
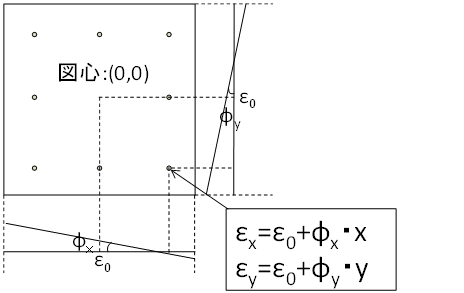
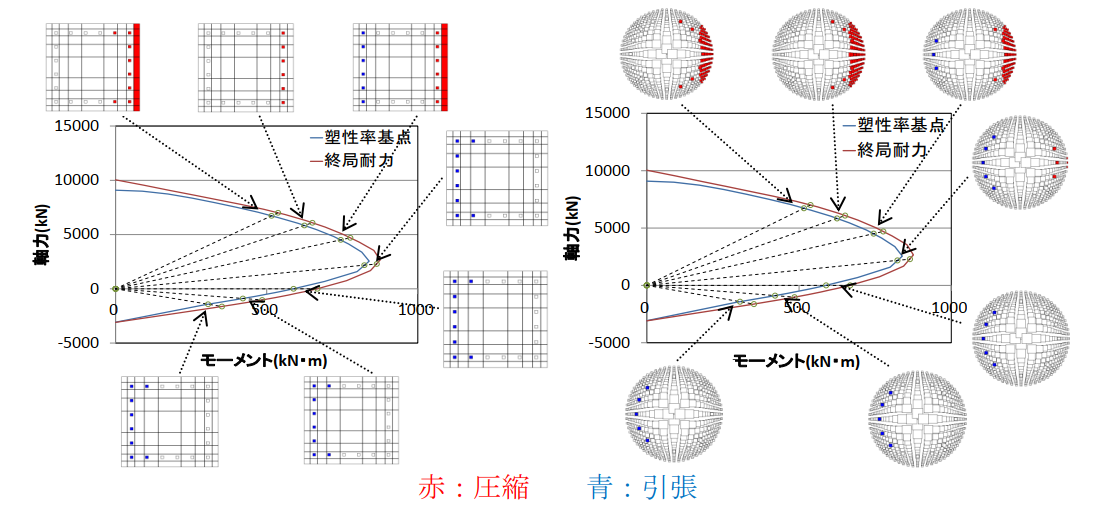
軸力の違いによる塑性率基点時断面塑性化状況の例
(3) 降伏発生時を塑性率基点にする方法
いずれかの分割断面が塑性率1を超えた時点を塑性率基点として塑性率を計算します。 鉄筋降伏やコンクリート圧壊、鉄骨の縁降伏発生時が塑性率1となるため、弾性限耐力をクライテリアとする場合に向いています。
塑性率は、最大応答曲率/塑性率基点曲率で計算されます。 この計算方法の場合、曲げ塑性率と軸塑性率は同じ値になります。 また、塑性率が1を下回る場合は評価されません。
間柱ダンパー
間柱ダンパー
間柱ダンパーは支持部とダンパー部からなる3分割要素としてモデル化されます。ダンパー部は制震部材の特性により、履歴型の非線形ばねや速度依存型のダッシュポットとしてモデル化されます。支持部については部材非線形性が考慮されます。その際、軸力は0と仮定して算出します。
耐震壁
耐震壁
耐震壁は、壁エレメントモデルの間柱部分にファイバー梁要素を適用した、ファイバー型壁エレメントモデルにより行います。軸・曲げについてはファイバー断面により非線形特性を評価し、せん断については各せん断耐力式に基づいた非線形性を採用します。
鉄筋コンクリート造耐震壁
鉄筋コンクリート造耐震壁の非線形特性(軸、曲げ)
壁柱部分は両端ファイバー梁要素とし、求めた断面性能は梁要素全体に均等に分布していると仮定します。両端ファイバー要素の非線形特性については、柱の項(ファイバーモデル)を参照してください。
鉄筋コンクリート造耐震壁の非線形特性(せん断)
鉄筋コンクリート造耐震壁のせん断非線形特性は、下図に示すトリリニアモデルで評価します。
(1)せん断ひび割れ強度( $Q_c$)
鉄筋コンクリート造耐震壁のせん断ひび割れ強度( $Q_c$)は下式で算定します1)。
$$Q_c = (0.043 \cdot p_g+0.051) \cdot F_c \cdot A_w$$$A_w$:壁体断面積(cm2)
$p_g$:引張側最端の柱1本の主筋量(cm2)/ $A_w$(%)
$F_c$:コンクリートの設計基準強度(kg/cm2)
(2)せん断降伏時剛性低下率( $β_u$)
鉄筋コンクリート造耐震壁のせん断降伏時剛性低下率( $β_u$)は下式により求めます1)。
$$\beta_u = 0.46 \cdot p_w \cdot \sigma_y/F_c+0.14$$$p_w$:壁の縦筋比
$σ_y$:壁筋の降伏強度(kg/cm2)
$F_c$:コンクリートの設計基準強度(kg/cm2)
(3)終局せん断強度( $Q_u$)
RC造耐震壁の終局せん断降伏強度( $Q_u$)は、付帯柱の主筋を考慮して次のいずれかの式で算定します2)。開口に対してはせん断耐力の低減率( $r$)を考慮します。
$$Q_u = \left( \frac{0.053 p_{te}^{0.23}(F_c+18)}{M/(Q \cdot D)+0.12}+0.85 \sqrt{\sigma_{wh} \cdot p_{wh}} +0.1\sigma_0 \right) t_e \cdot j \cdot r$$ $$Q_u = \left( \frac{0.068 p_{te}^{0.23}(F_c+18)}{ \sqrt{M/(Q \cdot D)+0.12}}+0.85 \sqrt{\sigma_{wh} \cdot p_{wh}} +0.1\sigma_0 \right) t_e \cdot j \cdot r$$1) 国土交通省:2007年版建築物の構造関係技術基準解説書;P.635-637,2007.8
2) 国土交通省:2007年版建築物の構造関係技術基準解説書;P.281-282,638-639,2007.8
$t_e$:耐震壁のI形断面を長さと断面積とが等しい等価断面に置き換えたときの幅( $t_e$)で、壁厚(t)の1.5倍以下とする。
$M/(Q・D)$:シアスパン比
$M/(Q・D)$<1の場合は1、 $M/(Q・D)>3$の場合は3とする。
$D$:付帯柱を含めた耐震壁の全長(mm)
$j$:応力中心間距離(= $7/8・d$)(mm)
$p_{te}$:等価引張鉄筋比(= $a_t/(t_e・d)・100$)(%)
$a_t$:引張側柱の主筋断面積(mm2)
$d$: $D-Dc/2$( $Dc$:圧縮側柱のせい)(mm)
$σ_{wh}$:水平せん断補強筋の材料強度(N/mm2)
$p_{wh}:t_e$を厚さと考えた場合の水平せん断補強筋比
(小数、1.2%を超える場合は1.2%とする)
$p_{wh} = P_{wh} \cdot t/t_e/100$$P_{wh}$:横筋比
$t$:壁厚(mm)
$r$:せん断耐力の低減率
$r = 1- \max \left( r_0, \frac{l_0}{l_w}, \frac{h_0}{h} \right)$$h_0$:開口部の高さ(m)
$l_0$:開口部の幅(m)
$l_w$:付帯柱の中心間距離(m)
$h$:壁の上下梁の中心間距離(m)
$r_0$:開口周比
$r_0 = \sqrt{ \frac{h_0 \cdot l_0}{h \cdot l_w}}$
$σ_0$:全断面積に対する平均軸方向応力度(=N/A)(N/mm2)
$N$:軸力(N)
$A$:側柱および壁板の軸断面積(mm2)
3) 日本建築学会;鉄筋コンクリート終局強度設計に関する資料;P.132,1987.9
耐震壁がスパン方向で連続する場合、それらを一枚としてせん断耐力の計算を行います。ただし、耐震壁は同一直線状に並んでいることを条件とします。
連スパンの壁は以下のように取り扱います。
- 連スパンの壁が一体とみなして耐力を計算し、せん断断面積の比率で耐力を分配します。
- 横筋比は、各壁の横筋比×横筋強度をせん断断面積で重み付け平均して用います。
- 開口がある場合、各壁の開口率を各壁のせん断断面積で重み付け平均した開口率を連スパンの開口率とみなします。
鉄骨鉄筋コンクリート造耐震壁
鉄骨鉄筋コンクリート造耐震壁の非線形特性(せん断)
SRC造耐震壁の終局せん断降伏強度( $Q_c$)は以下の3式のいずれかまたは鉄骨部分を無視してRC造耐震壁として計算します。SRC造耐震壁として計算する場合には、耐震壁が連続する場合でもそれぞれ単独の耐震壁として計算されます。
(1) せん断ひび割れ強度( $Q_c$)
鉄筋コンクリート造耐震壁と同様に計算します。
(2) せん断降伏時剛性低下率( $β_u$)
鉄筋コンクリート造耐震壁と同様に計算します。
(3) 終局せん断強度( $Q_u$)
a) SRC規準
各スパンの耐震壁を内部耐震壁、外部耐震壁に大別します。
内部耐震壁の判定は下記のルールで行い、下記のいずれにも該当しない場合は外部耐震壁とします。
・上下左右を耐震壁で囲まれている。
・上及び左右を耐震壁で囲まれており、下側節点のいずれかの節点がフリー以外の状態となっている。
せん断耐力は下記により計算します。
$_wQ_u$ = max ( $_wQ_u$ $_1$, $_wQ_u$ $_2$)
$_wQ_u$ $_1$ = $r \cdot t \cdot l \cdot _wf_s$
$_wf_s = \min (0.067Fc,1.0+Fc/50)$$_wQ_u$ $_2$ = $r \cdot _wp \cdot _w\sigma_y \cdot t \cdot l'$
$_wQ_u$ $_2$ = $r \cdot _wf \cdot s' \cdot t \cdot l'$
$_wf \cdot s' = \min (0.25Fc,1.13 \sqrt{Fc})$b) SRC診断規準式
せん断耐力は下記により計算します。
$$Q_u = \left( \frac{0.053 p_{ge}^{0.23}(F_c+18)}{\frac{hw}{2l}+0.12}+0.85 \sqrt{\sigma_{wh} \cdot _{r}p_{se}} +0.1\sigma_{0e} \right) b_e \cdot l_w \cdot r$$ただし、
$1 \leq \frac{hw}{2l} \leq 3$$p_{ge}$:引張側柱の等価引張鋼材比(%)。ただし、0.1%以下の場合0.1%とする。
$_rp _{se}$ = $a _w/(b _e・s)$ + $Σ{a _ {tg}/(b_e・h')・(_rbσ _y/_wσ _y)}$ ただし、 $_rp _{se}$≦ $2a_w/(be・s)$
$a_{w,s}$ :1組の横筋の断面積および間隔
$a_{tg}$:計算している壁の床位置から高さが $l_{w0}$以内にある梁断面の鉄骨及び主筋の全断面積
$h_w$:検討階より連層耐震壁最上階までの高さ。検討階が最上階なら2倍とする。
$σ_{0e}$ : $N/(b_e・l)$
$l_w$ :柱芯間距離
$h_w$計算時の連層耐震壁は下階から上階に耐震壁配置基準節点番号が連続する場合に連層とみなします。連スパン耐震壁の場合は連スパン耐震壁を一体とみなし、基準節点番号が連続するかどうかで判定します。
c) 構造関係技術基準解説書
せん断耐力は下記により計算します。
$$_wQ_u = _wQ+\Sigma{_c}Q_u$$ $_wQ = \min (_wp \cdot _w\sigma_y,Fc/4 ) \cdot t \cdot l'$$_cQ_u = b \cdot _rj (1.5fs+0.5_rp_w \cdot _r\sigma_w$ $_y$) + $_sA_w \cdot _s\sigma_y/ \sqrt{3}$
$f_s = \min ( Fc/20,(0.5+Fc/100) \cdot 1.5 ) $耐震壁の中間に柱が存在する場合、 $_cQ_u/2$としてそれぞれの壁耐力に加算します。
鋼板耐震壁
鋼板耐震壁は弾性としてモデル化されます。 付帯柱をピンとするか剛接とするか、計算条件で指定できます。
ブレース
ブレース
ブレースは、隣接する階の異なる2つの節点を端点として定義し、軸バネにモデル化します。ブレースに関する基本事項を以下に示します。
■ブレース断面は一様として断面性能および耐力を算定します。
■端部はピン接合とし、軸力のみを負担するものとします。ただし、「面内に拘束する」とした場合には面外方向には剛接合となります。
鉄骨ブレース
鉄骨造ブレースの軸非線形特性
鉄骨造ブレースの軸非線形特性は、下図に示すバイリニアモデルで評価します。
引張耐力および圧縮耐力は指定により下記から選択可能です。
終局耐力(Nu)
$$N_u = \sigma_y \cdot A_n$$$σ_y$:降伏点強度(N/mm2)
$A_n$:全断面積(mm2)
許容応力度( $N_a$)
鉄骨ブレースの許容応力度は、鋼構造設計指針により次式で算定します2)。
引張
$$N_a = \sigma_{as} \cdot A_n$$$σ_{as}$:短期許容応力度(N/mm2)
$A_n$:全断面積(mm2)
圧縮
$$N_a = f_{cS} \cdot A_n$$
圧縮材の座屈の長期許容応力度( $fc_L$)は次式で算定します。なお、圧縮材の座屈の短期許容応力度( $fc_S$)は長期許容応力度( $fc_L$)の1.5倍とします。
$$ fc_L = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \frac{F}{\nu} \left( 1-0.4 \cdot \left( \frac{\lambda}{\Lambda} \right)^2 \right) & \displaystyle \left( \lambda \leq \Lambda \right) \\ \displaystyle \frac{\frac{18}{65} \cdot F}{ \left( \frac{\lambda}{\Lambda} \right)^2} & \displaystyle \left( \Lambda < \lambda \right) \end{array} \right. \end{align}$$
$fc_L$:圧縮材の座屈の長期許容応力度
$F$:鋼材の規準強度(N/mm2)
$λ$:有効細長比(= $l_k/i$)
$i$:座屈軸についての断面2次半径(mm)
$l_k$:有効座屈長さ(mm)
$Λ$:限界細長比
$ν$:安全率
$\Lambda = \frac{1500}{\sqrt{\frac{F}{1.5}}}$ $\nu = \frac{3}{2}+\frac{2}{3} \left( \frac{\lambda}{\Lambda} \right)^2$安定座屈耐力 $N_{sb}$
鉄骨ブレースの安定座屈耐力は次式で算定します。
$$ N_{sb} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \sigma_y \cdot A_n & \displaystyle \left( \lambda_B \leq 0.15 \right) \\ \displaystyle \frac{\sigma_y \cdot A_n}{11\lambda_B-0.65} & \displaystyle \left( 0.15 < \lambda_B \leq 0.3 \right)\\ \displaystyle \frac{\sigma_y \cdot A_n}{6\lambda_B-0.85} & \displaystyle \left( 0.35<\lambda_B \right) \end{array} \right. \end{align}$$$K_b$ : $0.75$
$\lambda_B = \frac{K_b \cdot L}{i} \cdot \sqrt{\frac{\sigma_y}{\pi^2E}}$
座屈拘束ブレース(直接入力)の軸非線形特性
座屈拘束ブレース(直接入力)の軸非線形特性は、下図に示すバイリニアモデルで評価します。
座屈拘束ブレースの場合、引張および圧縮耐力は次式によります。
$$N_{y} = A_{n} \cdot \sigma_{y}$$メーカー製品ダンパーブレースの軸非線形特性
“制振要素"をご参照ください。
「制振要素」
1) 日本建築学会:鋼構造限界状態設計指針・同解説;P.20, 2010.2
2) 日本建築学会:鋼構造設計基準;1999.4
免震支承材
免震支承材
マルチシアスプリング要素
弾性すべり支承を除いた免震部材はマルチシアスプリング要素でモデル化します。(ただし、静的解析時は弾性すべり支承もマルチシアスプリングでモデル化されます。)
「剛性条件」「免震部材のモデル化」で「せん断力によって発生するモーメントを考慮する」とした場合には剛域付きせん断ばねとしてモデル化し、「せん断力によって発生するモーメントを考慮しない」とした場合には剛域なしのせん断ばねとしてモデル化します。
剛梁付きせん断ばね マルチシアスプリング要素
マルチシアスプリングは各方向の特性を同一にするためのモデル化であり、バネ本数を増やすとその分各ばねの剛性および耐力の低減率が変化します。RESP-Dにおけるマルチシアスプリングは常に8本としてモデル化されます(ただし、弾性でばねを分散させる必要がない天然ゴム系積層ゴムは2本としてモデル化されます。)
剛性低減率: $\frac{2}{n}$
耐力低減率: $\frac{1}{ \sum_{i=1}^{n/2} \left( \cos \left( \frac{\pi}{n} \cdot (i-1) \right)+ \sin \left( \frac{\pi}{n} \cdot (i-1) \right) \right)}$
参考までに各ばね本数と低減率を示します。
| 本数 | 2 | 4 | 6 | 8 | 16 |
|---|---|---|---|---|---|
| 剛性低減率 | 1.00000 | 0.50000 | 0.33333 | 0.25000 | 0.12500 |
| 耐力低減率 | 1.00000 | 0.41421 | 0.26795 | 0.19891 | 0.09849 |
摩擦ばね要素
弾性すべり支承は摩擦ばねによりモデル化します。摩擦ばねはバイリニアばねでモデル化された擬似的な摩擦要素です。摩擦によって変位が固定されたり、滑ったりする状況を擬似的に表現します。マルチシアスプリングとの違いは、以下になります。
・剛性低下(滑り出し)の判定がベクトルとしての合力で評価されます。
・発生するせん断力による曲げを伝達しません。
例えば、マルチシアスプリングで摩擦を表現した場合、純粋なX方向加力で滑り出したとしてもY方向に対してはまだ剛性を有した状態になります。一方で摩擦ばねではベクトルの合力により滑りを判定するため、滑り状態に達していればどの方向に対しても剛性低下した状態として評価できます。
発生する水平力は下記のようになります。
$$ Q = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle K_1 \times \delta & \displaystyle \left( Q < Q_{max} \right) \\ \displaystyle Q_{max} & \displaystyle \left( Q_{max} \leq Q \right) \end{array} \right. \end{align}$$$Q_{max}$:最大摩擦力 $( = μ×N )$
$μ$ :摩擦係数
$N$ :長期軸力
指定により、変動軸力を考慮可能です。 考慮した場合、計算安定性が損なわれる場合があります。
$K1$ :弾性剛性
$δ$ :水平変位
06. 終局検定
06. 終局検定のサブセクション
採用応力
採用応力
採用応力は"断面算定-採用応力"に準じます。
柱の曲げ余裕度は2軸曲げとして、以下の様に計算しています。
$$ \frac{1}{\left( \left( \frac{M_{m_x}}{M_{u_x}} \right)^{\alpha_x}+ \left( \frac{M_{m_y}}{M_{u_y}} \right)^{\alpha_y}\right)^{ \frac{1}{\alpha}}}$$| 断面 | αx | αy | α | 備考 |
|---|---|---|---|---|
| RC | 2.0 ※ | 2.0 ※ | 2.0 ※ | |
| SRC | 2.0 | 2.0 | 2.0 | |
| CFT | 2.0 | 2.0 | 2.0 | |
| S(H型) | 2.0 | 1.0 | 2.0 | 強軸をXとする |
| S(H型以外) | 2.0 | 2.0 | 2.0 |
※ RCのαは終局検定条件で変更可能。
柱のせん断余裕度は、RCのみ指定により2軸せん断として、以下の様に計算しています。
$$ \frac{1}{\left( \left( \frac{Q_{m_x}}{Q_{u_x}} \right)^{\alpha_x}+ \left( \frac{Q_{m_y}}{Q_{u_y}} \right)^{\alpha_y}\right)^{ \frac{1}{\alpha}}}$$| 断面 | αx | αy | α | 備考 |
|---|---|---|---|---|
| RC | 2.0 ※ | 2.0 ※ | 2.0 ※ | |
| SRC | - | - | - | |
| CFT | - | - | - | |
| S(H型) | - | - | - | |
| S(H型以外) | - | - | - |
※ RCのαは終局検定条件で変更可能。
共通事項
軽量コンクリート使用時のせん断耐力低減
軽量コンクリートを使用している部材のせん断終局耐力は、以降の式による計算で求められた耐力に対して0.9を乗じた数値を採用します。
鉄筋コンクリート梁の終局耐力
鉄筋コンクリート造梁の終局耐力
大梁検定表の符号一覧
鉄筋コンクリート造の大梁終局検定表の符号一覧を以下に示します。
[塑性理論式]
$B$:梁幅(mm)
$D$:梁せい(mm)
$_t$:引張縁から引張鉄筋重心までの距離(mm)
$L$ : 部材長,内法長さ(mm)
$a_t$:引張鉄筋の断面積(mm2)
$j_t$ : 応力中心間距離
$p_t$:引張鉄筋比(%)
$p_w$:せん断補強筋比(%)
$M_u$:終局曲げ強度(kN・m)
$Q_{mu}$:両端ヒンジを仮定した場合の終局せん断応力(kN)
$= \frac{\left( M_{u \textup{上}}+M_{u \textup{下}} \right) × \textup{上限強度倍率}}{ \textup{部材長(内法)}}$
$Q_L$:長期せん断応力(kN)
$Q_E$:水平荷重時せん断応力(kN)
$α$:せん断力割増率、ユーザー指定によります注1)。
$Q_{su}$:せん断破壊によって決定するせん断耐力(kN)
$α_{su}$:せん断に対する検定値(= $Q_{su}/Q_D$)
$Q_{bu}$:付着割裂破壊によって決定するせん断耐力(N)
$α_{bu}$:付着に対する検定値(= $Q_{bu}/Q_D$)
$τ_{bu}$:1段目主筋の付着信頼強度(N/mm2)
$τ_f$:設計用付着応力度(N/mm2)
$α_t$:梁の上端筋に対する付着強度低減係数
$b_{si2}$:2段目の割裂長さ比
$k_{st2}$:2段目主筋に対する横補強筋効果
$τ_{bu2}$:2段目主筋の付着信頼強度(N/mm2)
$L_d$:必要付着長さ(mm)
注1) 「設計・計算条件」→「増分解析条件」→「部材耐力式・終局検定設定」参照。
[靭性指針式]
$B$:梁幅(mm)
$D$:梁せい(mm)
$d_t$:引張縁から引張鉄筋重心までの距離(mm)
$L$ : 部材長,内法(mm)
$σ_y$:主筋の信頼強度算定用強度(N/mm2), 鉄筋材料強度×信頼強度倍率
$σ_{yu}$:主筋の上限強度算定用強度(N/mm2), 鉄筋材料強度×上限強度倍率
$j_e$:トラス機構に関与する断面の有効せい(mm)
$b_e$:トラス機構に関与する断面の有効幅(mm)
$μ$:トラス機構の角度を表す係数( $=2-20R_p$)
$R_p$:終局限界状態でのヒンジ領域の回転角(rad)
$ν$:コンクリート圧縮強度の有効係数( $=(1-20R_p)ν_0$)
$ν_0$:降伏ヒンジ・潜在ヒンジを計画しない時の有効係数 $\left( =0.7-\frac{σ_B}{200}\right)$
$σ_B$:コンクリートの圧縮強度(N/mm2)
$p_{we}$:有効横補強筋比(%)( $=a_w/b_{es}$)
$a_w$:1組の横補強筋の断面積(mm2)
$s$:横補強筋の間隔(mm)
$tanθ$:アーチ機構の圧縮束の角度のタンジェント
$Q_L$:長期せん断応力(kN)
$Q$:両端ヒンジ時せん断力もしくは長期を除いた設計用せん断力
$V_{u1}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.1)の値(kN)
$V_{u2}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.2)の値(kN)
$V_{u3}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.3)の値(kN)
$Vu$:せん断信頼強度( $=min(V_{u1}, V_{u2}, V_{u3})$)
$V_{bu}$:付着破壊の影響を考慮したせん断信頼強度(kN)
$k_{st}$:1段目主筋に対する横補強筋効果
$k_{st2}$:2段目主筋に対する横補強筋効果
$Δσ$:1段目主筋の終局限界状態における部材両端部の応力度の差(N/mm2)
$Δσ2$:2段目主筋の終局限界状態における部材両端部の応力度の差(N/mm2)
$τ_{bu}$:1段目主筋の付着信頼強度(N/mm2)
$τ_f$:1段目主筋の設計用付着応力度(N/mm2)
$τ_{bu2}$:2段目主筋の付着信頼強度(N/mm2)
$τ_{f2}$:2段目主筋の設計用付着応力度(N/mm2)
鉄筋コンクリート造梁の終局耐力
終局検定においては、非線形解析モデルによる荷重増分解析結果に対し、以降に示す終局耐力を用いて検定を行います。
a) 梁の曲げひび割れ強度( $M_c$)、曲げ終局強度( $M_u$)
鉄筋コンクリート造梁の曲げひび割れ強度( $M_c$)および曲げ終局強度( $M_u$)については、非線形解析モデル(「曲げひび割れ強度」、「曲げ終局強度」)を参照してください。
b) 梁の塑性理論式による終局せん断強度( $Q_u$)
「終局耐力条件」で「終局強度型設計指針」を選択した場合、鉄筋コンクリート造梁の終局せん断強度( $Q_u$)は、塑性理論式により算定します。
付着に対する設計では、付着強度の確保(付着信頼強度( $τ_{bu}$)>設計用付着応力度 ( $τ_f$)が原則ですが、部材の耐力、変形性能が損なわれない範囲であれば付着ひび割れの発生、付着すべりの増大あるいは付着応力度の低下は許容することができるとされています1)。
本プログラムでは、終局時のせん断力に対してせん断強度、変形性能が損なわれないことの確認として以下の検定を行い、付着に関する数値( $τ_{bu},τ_f$)は参考として表示します。
$(Q_{su}-Q_L)/a \cdot Q_E \geq 1.0 \quad or \quad (Q_{su}-Q_L)/Q_{mu} \geq 1.0 $ せん断に対する余裕率
$(Q_{bu}-Q_L)/a \cdot Q_E \geq 1.0 \quad or \quad (Q_{bu}-Q_L)/Q_{mu} \geq 1.0 $ 付着に対する余裕率
※MK785, SPR785, SPR685を使用した場合、 $Q_L=Q_0$と読み替えて計算します。
$$Q_{su} = b \cdot j_t \cdot p_w \cdot \sigma_{wy} \cdot \cot \phi+k_1 \cdot (1-k_2) \cdot b \cdot D \cdot \nu \cdot F_c$$$k_1 = \frac{\sqrt{(L/D)^2+1}-(L/D)}{2}$
$k_2 = \frac{2 \cdot p_w \cdot \sigma_{wy}}{\nu \cdot F_c}$
$ \nu = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle (1.0-15 \cdot R_p) \cdot \nu_0 & \left(0 < Rp \leq 0.05 \right) \\ \displaystyle 0.25 \cdot \nu_0 & \left( 0.05 < Rp \right) \end{array} \right. \end{align}$
$ν_0 = 0.7- \frac{F_c}{200}$
$ \cot \phi = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle 2.0-50 \cdot Rp & \left(0 < Rp \leq 0.02 \right) \\ \displaystyle 1.0 & \left( 0.02 < Rp \right) \end{array} \right. \end{align}$
$Q_{su}$:せん断破壊によって決定するせん断耐力(N)
$b$:部材幅(mm)
$j_t$:主筋の重心間距離(mm)
$p_w$:せん断補強筋比(小数)
$σ_{wy}$:せん断補強筋の降伏強度算定用強度(N/mm2)
$L$:内法長さ(mm)
$D$:部材せい(mm)
$F_c$:コンクリートの設計基準強度(N/mm2)
※ $k_2≦1.0$とします。
※ $p_w・σ_{wy}≦ν・F_c/2$とします。
※ $ν,p_w,σ_{wy}$は次項の表によります。 $p_w$で上限を超える場合は上限値とします。
1 ) (社)日本建築学会:鉄筋コンクリート造建物の靭性保証型耐震設計指針・同解説;P.177,1997.7
| 製品名 | σwy(N/mm2) | Pw | ν |
|---|---|---|---|
| ウルボン【SBPD1275/1420】 | $min(25・Fc,1275)$ | $~1.2%$ $(~0.8\%^{*1})$ | $0.7(1.0-F_c/140)$ |
| リバーボン1275【SBPDN1275/1420】 | $~1.2\%$ | ||
| ウルボン785【UB785】 | $min(25・Fc,785)$ | $0.7(0.7-F_c/200)$ | |
| リバーボン785【KW785】 | |||
| スミフープ、ストロングフープ、 デーフープ【KSS785】 | |||
| UHYフープ【SHD685】 | $min(25・Fc,685)$ | ||
| エヌエスハイデック685H【HDC685】 | $685$ | ||
| スーパーフープ【KH785】 | $25・F_c ・・・(F_c<27.4)$ $ 785 ・・・(27.4≦F_c)$ | ||
| パワーリング785【SPR785】 | $25・F_c$
$・・・(F_c<32.0)$ $785 ・・・(32.0≦F_c)$ | ||
| パワーリング685【SPR685】 | $min(25・Fc,685)$ | ||
| エムケーフープ785【MK785】 | $25・F_c$
$・・・(F_c<31.4)$ $785 ・・・(31.4≦F_c)$ | ||
*1:柱において $F_c 27(N/mm^2)$未満の場合。
$Q_{bu}$:付着割裂破壊によって決定するせん断耐力(N)
$Q_{bu} = j_t \cdot \tau_{bu} \cdot \sum \phi+k_1 \cdot (1-k_3) \cdot b \cdot D \cdot \nu \cdot F_c$
$k_3 = \frac{2 \cdot \tau_b \cdot \sum \phi}{b \cdot \nu \cdot F_c}$
$τ_{bu}$:1段目主筋の付着信頼強度(N/mm2)
| 商品名 | 計算式 |
|---|---|
| リバーボン785【KW785】 | $τ_{bu} = k_0 \cdot 0.313 \left( 0.307b_1+0.427+ \frac{24.9a_w \cdot h}{x \cdot N \cdot d_b} \right) \cdot \sqrt{F_c}$ |
| スミフープ、ストロングフープ、 デーフープ【KSS785】 | |
| UHYフープ【SHD685】 | |
| エヌエスハイデック685H【HDC685】 | |
| ウルボン【SBPD1275/1420】 | $τ_{bu} = k_0 \cdot \left( 0.0961b_1+0.134+ \frac{7.8a_w \cdot h}{x \cdot N \cdot d_b} \right) \cdot \sqrt{F_c}$ |
| リバーボン1275【SBPDN1275/1420】 | |
| ウルボン785【UB785】 | |
| スーパーフープ【KH785】 | |
| パワーリング785【SPR785】 | |
| パワーリング685【SPR685】 | |
| エムケーフープ785【MK785】 | |
| 異径鉄筋 | $τ_{bu} = a_t \cdot \left( (0.085b_1+0.10) \cdot \sqrt{F_c}+k_{st} \right)$ $a_t =\begin{align}\left\lbrace\begin{array}{ll}\displaystyle 0.75 - \frac{F_c}{400} & (梁の上端主筋) \\\displaystyle 1.0 & ( 上記以外)\end{array}\right.\end{align}$ $ k_{st} =\begin{align}\left\lbrace\begin{array}{ll}\displaystyle (54+45N_w/N_1)(b_{si}+1)p_w & \left(b_{ci} \geq b_{si} \right) \\ \displaystyle 140A_w/(d_bs) & \left( b_{ci} < b_{si}\right) \end{array} \right. \end{align} $ |
$Σφ$:引張鉄筋の周長和(2段筋,寄筋を含める)(mm)
$k_0$: $1.0$(梁)、 $1.22$(柱)
$a_w$:せん断補強筋の断面積(mm2)
$b_i$:割裂線長さ比 $(= \min (b_{vi},b_{ci},b_{si})$
$b_{vi} = \sqrt{3} \cdot \left( \frac{2 \cdot C_{\min}}{d_{b1}}+1 \right)$
$b_{ci} = \sqrt{2} \cdot \left( \frac{C_S+C_b}{d_{b1}}-1 \right)$
$b_{si} = \frac{b}{N \cdot d_{b1}}-1$
$C_{min}$:主筋のかぶり厚 $(=min(C_s,C_b))$(mm)
$C_s$:主筋の側面から側面までのかぶり厚さ(mm)
$C_b$:主筋の側面から底面までのかぶり厚さ(mm)
$d_{b1}$:1段目の主筋径(呼び名)(mm)
$h:b_i=b_{vi}$のとき $h = 0$
$b_i=b_{ci}$のとき $h = \sqrt{2}$
$b_i=b_{si}$のとき $h = 1.0+0.85 \cdot (n-2)/N$
$n$:1組のせん断補強筋の本数で、n>4の場合は4とします。
$x$:せん断補強筋ピッチ(mm)
$N$:外側一列の引張鉄筋の本数
2) (社)日本建築学会:鉄筋コンクリート造建物の靭性保証型耐震設計指針・同解説;P.175-181,1997.7
設計用付着応力度 $τ_f$、および2段目主筋の信頼強度 $τ_{bu2}$は、靭性指針2)に基づき算定します。
$\tau_f = d_b \cdot \Delta \sigma/(4 \cdot (L-d))$
$τ_f$:設計用付着応力度(N/mm2)
$⊿σ$:部材両端部の主筋の応力度の差。以下の計算により算出する。
$⊿σ= 2・σ_{yu}$ (両端ヒンジが発生している場合)
$⊿σ= σ_{yu}+σ_y$ (片端ヒンジが発生している場合)
$⊿σ= 2・σ_y$ (ヒンジが発生していない場合)
$d$:部材有効せい(圧縮縁から引張鉄筋重心位置までの距離)(mm)
$\tau_{bu2} = a_2 \cdot a_1 \cdot \left( (0.085 \cdot b_{si2}+0.10) \cdot \sqrt{F_c}+k_{st2} \right)$
$τ_{bu2}$:2段目主筋の付着信頼強度(N/mm2)
$α_2$:2段目主筋に対する強度低減係数(=0.6)
$α_t$:梁の上端筋に対する付着強度低減係数
$0.75+F_c/400$ (梁の上端主筋の場合)
$01$ (上記以外の場合)
$b_{si2}$:2段目主筋の割裂長さ比
$b_{si2} = (b-N_2 \cdot d_{b2})/(N_2 \cdot d_{b2})$
$N_2$:2段目の主筋本数
$b_2$:2段目の主筋径(呼び名)(mm)
$k_{st2}$:2段目主筋に対する横補強筋効果
$k_{st2} = 99 \cdot (b_{si2}+1) \cdot p_w$
付着設計における2段目主筋は、断面最外縁から部材せい $D$の $1/4$の範囲に配筋された主筋で、1段目主筋以外の主筋と定義します。
2段筋の必要付着長さ $L_d$は、RC規準による平均付着応力度の算定式を用いて求めます3)。下図に示すように、設計用付着応力度 $τ_f$は、検定断面の鉄筋の応力度 $σ_y$が検定断面から部材の有効せい $d$だけ離れた断面まで一定と見なし、B断面より一様な付着作用によって定着されるものと仮定します。よって、必要付着長さ $L_d$は検定断面を起点とする付着長さ $l_d$となります。
$L_d = \frac{\sigma_y \cdot a}{\tau_f \cdot \phi}+d$
$L_d$:必要付着長さ(mm)
$σ_y$:鉄筋の降伏強度(N/mm2)
$a$:鉄筋の断面積(mm2)
$τ_f$:設計用付着応力度(N/mm2)
$φ$:鉄筋の周長(mm)
3) 社)日本建築学会:鉄筋コンクリート構造計算規準・同解説;P.212-213,2010.2
c) 梁の靭性指針式による終局せん断信頼強度
「終局耐力条件」で「靭性保証型設計指針」を選択した場合、鉄筋コンクリート造梁の終局せん断信頼強度 $V_u$、付着破壊の影響を考慮したせん断信頼強度 $τ_{bu}$については、靭性指針4)により算定します。
また、設計用付着応力度 $τ_f$および2段目主筋の信頼強度 $τ_{bu2}$は、b)で前述した付着に対する設計と同様とします。
$V_u$:せん断信頼強度(N/mm2)
$V_u$= $min \left( V_{u1}, V_{u2}, V_{u3} \right)$
$V_{u1} = \mu p_{we}\sigma_{wy}b_ej_e+ \left( \nu \sigma_B- \frac{5p_{we}\sigma_{wy}}{\lambda} \right) \frac{bD}{2} \tan \theta$ (6.4.1)
$V_{u2} = \frac{\lambda \nu \sigma_B+p_{we}\sigma_{wy}}{3}b_ej_e$ (6.4.2)
$V_{u3} = \frac{\lambda \nu \sigma_B}{2}b_ej_e$ (6.4.3)
$μ$:トラス機構の角度を表す係数( $=2-20R_p$)
$R_p$:終局限界状態でのヒンジ領域の回転角(rad)
$p_w$:有効横補強筋比(%)( $=a_w/b_e$)
$a_w$:1組の横補強筋の断面積(mm2)
$s$:横補強筋の間隔(mm)
$σ_{wy}$:横補強筋の信頼強度(N/mm2)
$b_e$:トラス機構に関与する断面の有効幅(mm)
$j_e$:トラス機構に関与する断面の有効せい(mm)
$ν$:コンクリート圧縮強度の有効係数 $\left( =(1-20R_p)ν0 \right) $
$ν_0$:降伏ヒンジ・潜在ヒンジを計画しない時の有効係数 $\left( =0.7- \frac{σ_B}{200}\right)$
$σ_B$:コンクリートの圧縮強度(N/mm2)
$λ$:トラス機構の有効係数
$b$:梁幅(mm)
$D$:梁せい(mm)
$θ$:アーチ機構の圧縮束の角度
4) (社)日本建築学会:鉄筋コンクリート造建物の靭性保証型耐震設計指針・同解説;P.142-162,1997.7
※ $b_e$は下記によります。
柱およびスラブ付きでない梁の場合は、図6.4.1(a)(b)(c)に示すように、外側の横補強筋のせん断力直交方向への芯々間隔とします。
両側スラブ付きの梁の場合は、図6.4.1(d)に示すように、 $b_e=b$とします。
片側スラブ付きの梁の場合は、図6.4.1(e)に示すように、スラブのない側の横補強筋からスラブのある側のコンクリート表面までを $b_e$とします。
※λは下記(6.4.8)によります。
$\lambda = 1- \frac{s}{2j_e}- \frac{b_s}{4j_e}$ (6.4.8)
ここで、bsは次式で算定します。
$b_s = \frac{b_e}{N_s+1}$ (6.4.9)
$N_s$:中子筋の本数(本)
※θは下記によります。
引張軸力を受ける柱では $tanθ=0$とします。
それ以外の柱・梁で、 $L/D \geqq 1.5$ の部材では、次式で算定します。
$\tan \theta =0.9 \times \frac{D}{2L}$ (6.4.10)
$L$:クリアスパン長さ(mm)(図6.4.2参照)
$L/D<1.5$の部材では次式で算定します。
$\tan \theta =\frac{\sqrt{L^2-D^2}-L}{D}$ (6.4.11)
$V_{bu}$: 付着破壊の影響を考慮したせん断信頼強度(N/mm2)
$Vb_u = min(V_{bu1}, V_{bu2} )$
$V_{bu1} = T_xj_e+ \left( \nu \sigma_B- \frac{2.5T_x}{\lambda b_e} \right) \frac{bD}{2} \tan \theta$ (6.8.14)
$V_{bu2} = \frac{\lambda \nu \sigma_B}{2}b_ej_e$ (6.8.15)
$T_x$:部材単位長さあたりに負担できる付着力
降伏ヒンジを計画しない部材: $T_x = \tau _{bu} \sum \phi _1+\tau _{bu2} \sum \phi_2$ (6.8.16a)
降伏ヒンジを計画する部材: $T_x = (1-10R_p)(\tau _{bu} \sum \phi_1+\tau _{bu2} \sum \phi_2)$ (6.8.16b)
$\sum \phi_1$:1段目主筋の周長の合計
$\sum \phi_2$:2段目主筋の周長の合計
$ν$:コンクリートの有効圧縮強度 係数終局せん断信頼強度によります
鉄筋コンクリート柱の終局耐力
鉄筋コンクリート造柱の終局耐力
柱検定表の符号一覧
鉄筋コンクリート造柱の終局検定表の符号一覧を以下に示します。
[塑性理論式]
$B$:柱幅(mm)
$D$:柱せい(mm)
$d_t$:引張縁から引張鉄筋重心までの距離(mm)
$a_t$:引張鉄筋の断面積(mm2)
$L$ : 部材長、内法(mm)
$p_t$:引張鉄筋比(%)
$p_w$:せん断補強筋比(%)
$p_g$:主筋全断面積のコンクリート全断面積に対する比(%)
$M_{m1}$:正加力時の終局曲げ応力(kN・m)
$M_{m2}$:負加力時の終局曲げ応力(kN・m)
$M_{u1}$:正加力時の終局曲げ強度(kN・m)
$M_{u2}$:負加力時の終局曲げ強度(kN・m)
$Q_{m1}$:正加力時の終局せん断応力(kN)
$Q_{m2}$:負加力時の終局せん断応力(kN)
$Q_{su}$:せん断破壊によって決定するせん断耐力(kN)
$Q_{bu}$:付着割裂破壊によって決定するせん断耐力(kN)
$N_L$:長期柱軸力(kN)
$N_{m1}$:正加力時の終局時柱軸力(kN)
$N_{m2}$:負加力時の終局時柱軸力(kN)
$N_{ut}$:軸圧縮強度(kN)
$N_{uc}$:軸引張強度(kN) [靭性指針式]
$B$:柱幅(mm)
$D$:柱せい(mm)
$d_t$:引張縁から引張鉄筋重心までの距離(mm)
$a_t$:引張鉄筋の断面積(mm2)
$p_t$:引張鉄筋比(%)
$p_g$:主筋全断面積のコンクリート全断面積に対する比(%)
内法(mm)
$j_e$:トラス機構に関与する断面の有効せい(mm)
$b_e$:トラス機構に関与する断面の有効幅(mm)
$μ$:トラス機構の角度を表す係数( $=2-20R_p$)
$R_p$:終局限界状態でのヒンジ領域の回転角(rad)
$ν$:コンクリート圧縮強度の有効係数 $\left( =(1-20R_p)ν0 \right) $
$ν_0$:降伏ヒンジ・潜在ヒンジを計画しない時の有効係数 $\left( =0.7- \frac{σ_B}{200}\right)$
$σ_B$:コンクリートの圧縮強度(N/mm2)
$p_{we}$:有効横補強筋比(%)( $=a_w/b_{es}$)
$a_w$:1組の横補強筋の断面積(mm2)
$s$:横補強筋の間隔(mm)
$M_{m1}$:正加力時の終局曲げ応力(kN・m)
$M_{m2}$:負加力時の終局曲げ応力(kN・m)
$M_{u1}$:正加力時の終局曲げ強度(kN・m)
$M_{u2}$:負加力時の終局曲げ強度(kN・m)
$Q_L$:長期せん断応力(kN)
$Q$:両端ヒンジ時せん断力もしくは長期を除いた設計用せん断力
$V_{u1}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.1)の値(kN)
$V_{u2}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.2)の値(kN)
$V_{u3}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.3)の値(kN)
$V_{u}$せん断信頼強度( $=min(V_{u1}, V_{u2}, V_{u3})$) (kN)
$τ_{bu}$:1段目主筋の付着信頼強度(N/mm2)
$τ_f$:1段目主筋の設計用付着応力度(N/mm2)
$τ_{bu}$:2段目主筋の付着信頼強度(N/mm2)
$τ_{f2}$:2段目主筋の設計用付着応力度(N/mm2)
$V_{bu}$:付着破壊の影響を考慮したせん断信頼強度(kN)
$N_L$:長期柱軸力(kN)
$N_{m1}$:正加力時の終局時柱軸力(kN)
$N_{m2}$:負加力時の終局時柱軸力(kN)
$N_{ut}$:軸圧縮強度(kN)
$N_{uc}$:軸引張強度(kN)
OTM低減:応答転倒モーメントの低減係数
上下動係数:上下動を考慮した軸力の割増係数
鉄筋コンクリート造柱の終局検定においては、5章の非線形解析モデルによる荷重増分解析結果に対し、以降に示す終局耐力を用いて検定を行います。実際の解析時における曲げ復元力特性は5章の非線形解析モデルによるモデル化が採用され、下記の終局曲げ強度と必ずしも一致しないことにご注意ください。
a) 終局曲げ強度( $M_u$)
鉄筋コンクリート造柱の終局曲げ強度( $M_u$)は、引張側と圧縮側に各1段の主筋を配筋した略算式である、構造規定式(at式)1)またはACI規準による平面保持解析にて算定します。寄筋がある場合、寄筋も $at$に含んで計算します。
・構造規定式(at式)
$M_u = 0.8 \cdot a_t \cdot \sigma_y \cdot D+0.4 \cdot N \cdot D$
$M_u = 0.8 \cdot a_t \cdot \sigma_y \cdot D+0.5 \cdot N \cdot D \left( 1-\frac{N}{b \cdot D \cdot F_c} \right)$
$M_u = (0.8 \cdot a_t \cdot \sigma_y \cdot D+0.12 \cdot b \cdot D^2 \cdot F_c) \cdot \left( \frac{N_{\max}-N}{N_{\max}-0.4 \cdot b \cdot D \cdot F_c} \right)$
$N_{max}$:中心圧縮時終局強度( $-b・D・F_c+a_g・σ_y$)(N)
$N_{min}$:中心引張時終局強度( $-a_g・σ_y$)(N)
$a_g$:主筋全断面積(mm2)
$N$:軸方向力(N)
$a_t$:引張主筋断面積(mm2)
$b$:柱幅(mm)
$D$:柱せい(mm)
$σ_y$:主筋降伏強度(N/mm2)
$F_c$:コンクリートの設計基準強度(N/mm2)
・ACI規準(平面保持仮定)
降伏曲げモーメントは、圧縮側コンクリートの応力分布を「ACI318-95規準」による等価応力度ブロック法を用いて、下記の①~⑥の仮定に基づいて算出します。
① 降伏曲げモーメントは圧縮縁のコンクリートのひずみ度が終局ひずみ $ε_u=0.3%$に達するときの曲げモーメントとする。
② 断面内各点のひずみ度は、中立軸からの距離に比例する。(平面保持の仮定)
③ 鉄筋の応力-ひずみ度関係は、降伏ひずみ度以下では弾性とする。降伏ひずみ度以上では材料強度とする。
④ コンクリートは引張応力度を負担しない。
⑤ コンクリートの圧縮応力度とひずみ度の関係は下図による。
⑥ 各係数は以下による
$ β_1 = \begin{align} \left\lbrace \begin{array}{ll} 0.85 & \displaystyle \left( F_c \leq 4000 \psi \right) \\ 0.85-0.05・(Fc-4000)/1000 & \displaystyle \left( 4000 \psi < F_c < 8000 \psi \right) \\ 0.65 & \displaystyle \left( 8000 \psi \leq F_c \right) \end{array} \right. \end{align} $
$β_2=β1/2$
$β_3=0.85$
$ ※1 (N/mm^2) \rightarrow 145.04 psi$
矩形柱の主筋の配置は次のように認識します。
$x_i, y_i$:図心からの各鉄筋重心位置
$a_{xi}, a_{yi}$:各鉄筋断面積
$i=1$ :1段引張主筋
$i=2$ :2段引張主筋
1) 国土交通省:2007年版建築物の構造関係技術基準解説書;P.626-627, 2007.8
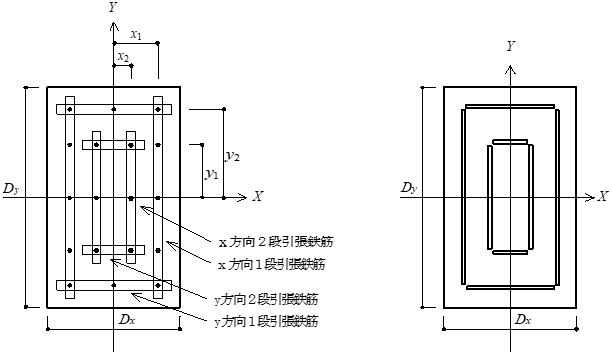
■隅部の鉄筋本数( $_{ck}N_i$)
$_{ck}N_i = \frac{2 \cdot (_{xk}n_i+ _{yk}n_i) - _{gk}N_i}{4}$
■引張鉄筋断面積( $_{jk}A$)
$_{jk}A = _{jk}a_1 \cdot _{jk}n_1 + _{jk}a_2 \cdot _{jk}n_2$
■鉄筋強度( $_{jk}Y$)
$_{jk}Y = ( _{jk} \sigma_{y1} \cdot _{jk}a_1 \cdot _{jk}n_1+_{jk}\sigma_{y2} \cdot _{jk}a_2 \cdot _{jk}n_2 )/_{jk}A$
$_{gk}N_i$:全鉄筋本数
$_{jk}a_i$:1本あたりの鉄筋断面積(mm2)
$_{jk}n_i$:鉄筋本数
$_{jk}σ_y$:鉄筋の降伏強度(N/mm2)
$i$:鉄筋径種類(i=1,2)
$j$:配置方向(j=X,Y)
$k$:1段筋または2段筋
b) 終局せん断強度( $Q_u$)
鉄筋コンクリート造柱の終局せん断強度( $Q_u$)は、鉄筋コンクリート造梁と同様に算定します(“採用応力"参照)。
鉄筋コンクリート造柱の余裕度は以下の様に計算しています。
$Q_{su}/Q_{mu} = \min (Q_{su}/Q_{mu1},Q_{su}/Q_{mu2})$
$Q_{bu}/Q_{mu} = \min (Q_{bu}/Q_{mu1},Q_{bu}/Q_{mu2})$
また、 $Q_D$と $Q_{mu}$については下記の違いがあります。
$Q_D = Q_L+a \times Q_E$
両端ヒンジを選択している場合: $Q_{mu}=(上限強度倍率)×(M_{iu}+M_{ju})/L$
存在応力を選択している場合: $Q_{mu}=Q_{L}+α×Q_{E}$
$M_{iu}$: 始端終局モーメント
$M_{ju}$: 終端終局モーメント
$Q_{mu}$: 両端ヒンジのせん断力
$L$: 危険断面位置間距離
c) 軸引張強度( $N_{ut}$),軸圧縮強度( $N_{uc}$)
鉄筋コンクリート造柱の軸圧縮強度( $N_{uc}$)、軸引張強度( $N_{ut}$)は構造規定2)に準じて算定します。本プログラムでは、圧縮軸力を正、引張軸力を負と表します。
$N_{uc} = b \cdot D \cdot F_c$
$N_{ut} = -a_g \cdot \sigma_y$
$N_{uc}$:軸圧縮強度(kN)
$N_{ut}$:軸引張強度(kN)
軸力に対する検定値は、以下のとおり算定します。OTM低減係数、上下動係数はユーザー指定によります。
スラブ筋断面積は「設計・計算条件」→「部材復元力特性条件」→「RC造大梁曲げ耐力計算方法」の設定を採用し、材料は「使用材料」→「その他」→「スラブ筋」の情報を採用します。
■長期軸力に対する検定
$N_L = N_{uc}$
■終局時軸力に対する検定
・ $min(N_{m1}$, $N_{m2})<0$または $max(N_{m1}$, $N_{m2})<0$の場合
$N_m / N_{ut}$
$N_m$:設計用柱軸力( $=min(N_{m1}, N_{m2})$または $max(N_{m1},N_{m2})$)(kN)
・ $min(N_{m1}, N_{m2})≧0$または $max(N_{m1},N_{m2})≧0$の場合
$N_m / N_{uc}$
$N_m$:設計用柱軸力( $=min(N_{m1}, N_{m2})$または $max(N_{m1}, N_{m2})$)(kN)
$N_m = N_L+|N_E| \cdot OTM \mbox{低減}+N_L \cdot \mbox{上下動係数}$
$N_L$:長期柱軸力(kN)
$N_{m1}$:正加力時の設計用柱軸力(kN)
$N_{m2}$:負加力時の設計用柱軸力(kN)
$N_E$:終局時柱軸力(kN)
国土交通省:2007年版建築物の構造関係技術基準解説書;P.626-627,629-630, 2007.8
注1) 「設計・計算条件」→「増分解析条件」→「部材耐力式・終局検定設定」参照。
鉄筋コンクリート接合部の終局耐力
鉄筋コンクリート造接合部の終局耐力
接合部検定表の符号一覧
鉄筋コンクリート造接合部の終局検定表の符号一覧を以下に示します。
$κ$ :接合部の形状による係数
$κ=1.0$ 十字形接合部
$κ=0.7$ ト形およびT形接合部
$κ=0.4$ L形接合部
$φ$ :直交梁の有無による補正係数
$φ=1.0$ 両側直交梁付き接合部
$φ=0.85$ 上記外の場合
$b_b$ :梁幅(大きい方)
$b_1$ :梁面から平行する柱側までの距離(左)
$b_2$ :梁面から平行する柱側までの距離(右)
$b_{a1}$ : $\frac{b_1}{2}$または $\frac{D}{4}$の小さい方
$b_{a2}$ : $\frac{b_2}{2}$または $\frac{D}{4}$の小さい方
$D_j$ :下側柱せい
$h_c$ :上階階高
$h_c$’ :下階階高
$T$ :上端鉄筋引張力(スラブ筋注1)含む)
$T'$ :下端鉄筋引張力
$M_{b}$:上端引張降伏モーメント
$M_{b'}$ :下端引張降伏モーメント
$Q_{cu}$ :上下柱の存在せん断力の平均
$Q_{du}$:梁降伏時の鉄筋引張降伏力 - 柱せん断力
$α$ :接合部せん断力の割増率( $=1.0$)
$V_{ju}$ :形状から計算される終局せん断耐力
鉄筋コンクリート造接合部の終局耐力
終局検定においては、5章の非線形解析モデルによる荷重増分解析結果に対し、以降に示す終局耐力を用いて検定を行います。ここで、TおよびT’は計算条件の指定により、両端ヒンジ時応力もしくは存在応力から選択できます。
$V_{ju} = \kappa \cdot \phi \cdot F_j \cdot b_j \cdot D_j$
$Q_{du} = a \cdot (T+T'-Q_{cu})$(柱せん断力:存在応力の場合)
$Q_{cu} = \frac{Q_{c1}+Q_{c2}}{2}$(柱せん断力:存在応力の場合)
$Q_{c1}$:上側柱せん断力
$Q_{c2}$:下側柱せん断力
$Q_{cu} = 2 \frac{M_b+M_b'}{h_c+h_c'}$(柱せん断力:大梁両端ヒンジの場合)
余裕率 : $V_{ju}/Q_{du}$
コンクリート充填鋼管(CFT)柱の終局耐力
CFT柱の終局検定用耐力は「コンクリート充填鋼管構造設計指針(以下、CFT指針)」に基づき算定します。なお、CFT指針において角型鋼管CFTは正方形のみを対象としていますが、本プログラムにおいては計算式を準用して長方形断面に対しても適用します。
(1) 共通事項
終局耐力を計算する際、各柱の寸法により柱を以下のように分類します。
A. 座屈長さが断面せいの4倍以下の場合 : 短柱
B. 座屈長さが断面せいの12倍を超える場合 : 長柱
C. 座屈長さが断面せいの4倍を超え、12倍以下の場合 : 中柱
(2) 軸方向力を受ける部材の終局耐力
A.短柱
座屈長さが断面せいの4倍以下の終局耐力 $N_{cu1}$は以下の式より算定します。
$N_{cu1} = {_c}N_c+(1+\xi){_s}N_c$
$\xi=0.27$:円形断面
$\xi=0$:角型断面
${_c}N_c = {_c}A \cdot F_c$
${_s}N_c = {_s}A \cdot F_y$
$_cA$:コンクリートの断面積
$_sA$:鋼管の断面積
$F_c$:コンクリートの設計基準強度
$F_y$:鋼管の降伏強度強さ
B.長柱
座屈長さが断面せいの12倍を超える柱の終局圧縮耐力 $N_{cu3}$は以下の式より算定します。
$N_{cu3} = _{c}N_{cr}+_{s}N_{cr}$
$_cN_{cr}$はコンクリート柱の座屈耐力で、以下の式により算定します。すなわち、座屈応力度 $_cσ_{cr}$にコンクリート部分の断面積 $_cA$を乗ずることにより算定します。
$_cN_{cr}=_c\sigma_{cr} \cdot _cA$
座屈応力度 $_cσ_{cr}$は以下のように算定します。
$$ \frac{_c\sigma_{cr}}{F_c} = \begin{align} \left\lbrace \begin{array}{ll} \frac{2}{1+ \sqrt{_c\lambda_1^4+1}} & \displaystyle \left( {_c}\lambda_1 \leq 1.0 \right) \\ 2 (\sqrt{2}-1) \exp ( C_c(1-_c\lambda_1 ) ) & \displaystyle \left( {_c}\lambda_1 \geq 1.0 \right) \end{array} \right. \end{align} $$$F_c$:コンクリートの設計基準強度
$_cλ_1$:規準化細長比で、以下の式より算定します。
${_c}\lambda_1 = \frac{{_c}\lambda}{\pi} \sqrt{\varepsilon_u}$
$_cλ$:コンクリート柱の細長比
$C_c$: $0.568+0.00612F_c$
$ε_u$:圧縮強度時ひずみで、以下の式より算定します。
$\varepsilon_u = 0.93 \cdot (Fc)^{\frac{1}{4}} \cdot 10^{-3}$
$_sN _{cr}$は鋼管柱の座屈耐力で、「鋼構造塑性設計指針」の以下の式に算定します。
$$ _sN_{cr} = \begin{align} \left\lbrace \begin{array}{ll} _sN_y & \displaystyle \left( _c\lambda_1 < 0.3 \right) \\ ( 1-0.545(_s\lambda_1-0.3) ) _sN_y & \displaystyle \left( 0.3 \leq _c\lambda_1 < 1.3 \right) \\ _sN_E/1.3 & \displaystyle \left( _c\lambda_1 \geq 1.3 \right) \end{array} \right. \end{align} $$ここに、
$_sN _{cr}$:降伏軸力(= $_sA・F_y$)
$_sλ_1$:規準化細長比で、以下の式より算定します。
${_s}\lambda_1 = \frac{{_s}\lambda}{\pi} \sqrt{\frac{F_y}{{_s}E}}$
$_sN _{cr}$:オイラー荷重で、以下の式より算定します。
${_s}N_E = \pi^2 \cdot {_s}E \cdot {_s}I/l_k^2$
$_sE$:鋼管のヤング係数
$l_k$ :座屈長さ
$_sI$ :鋼管の断面2次モーメント
$_sλ$:鋼管柱の細長比
C.中柱
座屈長さが断面せいの4倍を超え、12倍以下の柱の終局耐力 $N_{cu2}$はA.短柱で算定した $N_{cu1}$及び、B.長柱において $l_{k}/D=12$として算定した $N_{cu3}$を用い、以下の式より算定します。
$N_{cu2} = N_{cu1}-0.125(N_{cu1}-N_{cu3}) \cdot (l_k/D-4)$
また、軸方向引張力を受ける柱の終局軸耐力 $N_{cu2}$は、短柱、中柱、長柱を問わず、以下の式より算定します。
$N_{tu} = {_s}N_t$
ここで、
${_s}N_t = {_s}A \cdot \beta_2 \cdot F_y$
(3) 軸方向力および曲げモーメントを受ける部材の終局耐力
A.短柱の終局曲げ耐力
軸方向力と曲げモーメントを受ける座屈長さが断面せいの4倍以下の柱の終局耐力は、以下の式によって算定します。
$N_u = {_c}N_u+{_s}N_u$
$M_u = {_c}M_u+{_s}M_u$
(円形断面の場合)
$_cN_u = r_1^2(\theta- \sin \theta \cos \theta)_c\sigma_{cB}$
$_cM_u = \frac{2}{3}r_1^3 \sin^3\theta \cdot _c\sigma_{cB}$
$_sN_u = 2r_2t ( \beta_1\theta-\beta_2(\theta-\pi) ) F_y$
$_sM_u = 2r_2^2t(\beta_1-\beta_2) \sin \theta \cdot F_y$
$_c\sigma_{cB}=F_c+0.78 \cdot \frac{2t}{D-2t} \cdot F_y$
$r_1 = \frac{_cD}{2}$ 、 $r_2 = \frac{D-t}{2}$ 、 $\theta = \cos^{-1} (1-2x_n/_cD)$
$\beta_1 = 0.89$ 、 $\beta_2 = -1.08$ 、
$D$:鋼管のせい
$_cD$:コンクリートのせい
$F_c$:コンクリートの設計基準強度
$F_y$:鋼管の降伏強さ
$t$ :鋼管の板厚
$x_n$:コンクリートの圧縮縁から中立軸までの距離
(角形断面の場合)
$_cN_u = x_n \cdot _cD \cdot F_c$
$_cM_u = \frac{1}{2}(_cD-x_n)_cD \cdot x_n \cdot F_c$
$_sN_u = 2t(2x_n-_cD)F_y$
$_sM_u = Dt(D-t)F_y+2t(_cD-x_n) x_n \cdot F_c$
なお、中立軸がコンクリート断面外の場合の終局曲げ耐力は、上記の方法で得られる軸方向力と曲げモーメントの耐力曲線と、(2)「軸方向力を受ける部材の終局耐力」の終局軸圧縮耐力 $N_{cu1}$および終局軸引張耐力 $N_{tu}$を直線で補間することで算定します。
B.長柱の終局曲げ耐力
軸方向力と曲げモーメントを同時に受ける座屈長さが断面せいの12倍を超える柱を超える柱の終局耐力は以下の式より算定します。
・ $N_u \leq _cN_{cu}$ または、 $M_u \geq _sM_{u0} \left( 1- \frac{_cN_{cu}}{N_k} \right) \frac{1}{C_M}$ のとき、
$N_u = _cN_u$
$M_u = \left( _cM_u+_sM_{u0} \left( 1- \frac{_cN_{cu}}{N_k} \right) \frac{1}{C_M} \right)$ (1)
・ $N_u > _cN_{cu}$ または、 $M_u < _sM_{u0} \left( 1- \frac{_cN_cu}{N_k} \right) \frac{1}{C_M}$ のとき、
$N_u = _cN_{cu}+_sN_u$
$M_u = _sM_u \left( 1- \frac{_cN_{cu}}{N_k} \right) \frac{1}{C_M}$ (2)
ここに、
$_sM _{u0}$:鋼管部分が曲げモーメントのみを受ける場合の終局曲げ耐力
$_sN_u,_sM_u$ :鋼管長柱の終局耐力で以下によります。
$_sN_u = 2r_2t(2\theta- \pi)F_y$
$_sM_u = 4r_2^2t \sin \theta \cdot F_y$
上記式中の $_cN _{cu}$ は(2)「軸方向力を受ける部材の終局耐力」の $_cN _{cr}$あるいは $0.9_cN _{cr}$により、以下の式で算定します。 $_cM _u$が負になる場合には0として扱います。
$_cM_u = \frac{4_cN_u}{0.9_cN_{cr}} \left( 1 - \frac{_cN_u}{0.9_cN_{cr}} \right) _cM_{max}$
$_cM _{max}$:細長比 $_cλ_1$の 充填コンクリート長柱の最大曲げ耐力で、以下の式より算出します。
$_cM_{max} = \frac{C_b}{C_b+_c\lambda_1^2}_cM_{max0}$
$C_b=0.923-0.0045F_c$
$_cM _{max0}$は以下の式より算出します。
角型断面の場合: $_cM_{max} = \frac{F_c \cdot D^3}{8}$
円形断面の場合: $_cM_{max} = \frac{F_c \cdot D^3}{12}$
$N_k$は以下の式より算定します。
$N_k = \frac{\pi^2 \left( \frac{_cE' \cdot _cI}{5} +_sE \cdot _sI \right)}{l_k^2}$
ここに、 $_cE'$はコンクリートのヤング係数で以下の式を適用します。
$_cE' = (3.32 \sqrt{F_c}+6.90) \times 10^3$
$C_M$は節点移動がある場合の計算式として1.0とします。
C.中柱の終局曲げ耐力
軸方向力と曲げモーメントを同時に受ける座屈長さが断面せいの4倍を超え、12倍以下の柱の終局耐力は以下の式より算定します。
・ $N_u \leq _cN_{cu}$ または、 $M_u \geq _sM_{u0} \left( 1- \frac{_cN_{cu}}{N_k} \right) \frac{1}{C_M}$ のとき、
$N_u = _cN_{cu}$
$M_u = \left( _cM_u+_sM_{u0} \left( 1- \frac{_cN_{cu}}{N_k} \right) \frac{1}{C_M} \right)$
・ $N_u > _cN_{cu}$ または、 $M_u < _sM_{u0} \left( 1- \frac{_cN_{cu}}{N_k} \right) \frac{1}{C_M}$ のとき、
$M_u = _sM_{u0} \left( 1- \frac{N_u-_cN_{cu}}{N_{cu2}-_cN_{cu}} \right) \left( 1- \frac{_cN_{cu}}{N_k} \right) \frac{1}{C_M}$
(4) せん断を受ける部材の終局耐力
通常のせん断スパン比を有するCFT柱は材端に塑性ヒンジを形成する破壊状況を示すため、せん断の検定は行いません。
07. 非線形解析(動的解析)
07. 非線形解析(動的解析)のサブセクション
立体解析モデルの非線形特性
立体解析モデルの非線形特性
立体解析モデルの動的解析のための既定の非線形特性を部材、構造種別ごとに下表に示します。
| 部材種別 | 成分 | RC造・SRC造・CFT造 | S造 |
|---|---|---|---|
| 梁 | 曲げ | 武田型(トリリニア) | 標準型(バイリニア) |
| 軸方向 | 弾性 | 弾性 | |
| せん断 | 弾性 | 弾性 | |
| 柱 | 曲げ | ファイバーモデル*1 | ファイバーモデル*1 |
| 軸方向 | ファイバーモデル*1 | ファイバーモデル*1 | |
| せん断 | 弾性 | 弾性 | |
| 耐震壁 | 曲げ | ファイバーモデル | ― |
| 軸方向 | ファイバーモデル | ― | |
| せん断 | 原点指向型(トリリニア) | ― | |
| ブレース | 曲げ | ― | ― |
| 軸方向 | ― | 標準型(バイリニア)*2 | |
| せん断 | ― | ― |
*1:ファイバーモデルでは、鉄筋・鉄骨:標準型バイリニア、コンクリート:NewRCモデル(原点指向型)としてモデル化しています(ただし、NewRCの適用範囲であるFc60を超える強度、もしくはユーザー定義コンクリートの場合はBilinearの骨格曲線に対する原点指向型となります。適用範囲外のため、関数の形状が異常となるためです。)。また、指定により弾性とすることが可能です。
*2:指定により、非線形特性を個別に設定することが可能です。
鉄骨大梁の座屈を考慮した履歴
指定により、鉄骨大梁の座屈を考慮した履歴則を採用する事ができます。
座屈形式に応じて、以下の履歴則を採用します。
局部座屈
文献「加藤・秋山・帯: 局部座屈を伴うH形断面部材の変形, 日本建築学会論文報告集 第257号・昭和52年7月」を元に履歴則を設定します。
除荷特性は文献「孟・大井・高梨: 鉄骨骨組地震応答解析のための耐力劣化を伴う簡易部材モデル, 日本建築学会構造系論文報告集 第437号・1992年7月」によるROモデルを用います。
ROモデルの諸元は、γ=5, Φ=0.5とします。
横座屈
文献「井戸田・中田・吉田・小野: 横座屈で耐力が決まるH形鋼梁の繰返し履歴モデル,?日本建築学会構造系論文集?第80巻?第711号 819-829 2015年5月」を元に履歴則を設定します。
最大曲げ耐力 $M_u$ は以下のように計算します。
$$ \frac{\mu_{Mu}}{M_p}=\frac{2h_0}{1+c_{def}\lambda_b+(1+c_{res})\lambda_b^2+\sqrt{(1+c_{def}\lambda_b+(1+c_{res})\lambda_b^2)^2-4\lambda_b^2(1+c_{res}\lambda_b^2)}} $$ここで、
$c_{res}$ : 残留応力度の大きさを考慮する係数(=0.0)
$c_{def}$ : 初期たわみ量の大きさを考慮する係数(=
$q_{\kappa}k_{def}^r$)
$h_0$ : 塑性化後の歪み硬化による耐力上昇率
$f$ : 形状係数(=1.0)
$k_{res}$ : 降伏応力度に対する最大残留応力度の大きさの比率(=0.3)
$k_{def}$ : 部材初期たわみ量の正弦波成分の最大振幅を
$k_{def}・l_b/1000$ で表したときの係数(=1.0)
$\Lambda_c'$ : 基準化幅厚比と弾性限界細長比を用いて定義される変形性能指標(=
$( \lambda_b / _e\lambda_b + WF^3)^{1/3}$)
$h_0=\alpha_{\Lambda_c'}(\Lambda_c'-1.25)+1.0$ …
$(\Lambda_c'\leq1.25)$
$h_0=1.0$ …
$(\Lambda_c'\gt1.25)$
$q_{\kappa}=-0.1\kappa+0.065$ …
$(-1.0\leq\kappa\leq0.0)$
$q_{\kappa}=0.065$ …
$(0.0<\kappa)$
$r=0.5\kappa+1.0$ …
$(-1.0\leq\kappa\leq0.0)$
$r=1.0$ …
$(0.0<\kappa)$
連成座屈
文献「大谷・井戸田: 局部座屈と横座屈を考慮したH形鋼梁の繰返し履歴モデル, 日本建築学会構造系論文集 第84巻 第765号 1475-1484 2019年11月」を元に履歴則を設定します。
最大耐力
$M_u$ は、横座屈と同様に算出します。
耐力劣化の開始点は、論文中の
$\theta_{static}$ を採用します。
質点系解析モデルの非線形特性
質点系解析モデルの非線形特性
復元力特性のモデル化(上部構造)
初期剛性
本プログラムでは、増分解析の最初のポイント(第1ステップ)の荷重-変形関係から初期剛性(K1)を計算します。従って、荷重増分解析の第1ステップの状態で非線形領域に入ってしまう解析結果からは、初期剛性を正しく計算できません。特に、初期応力が過大なことによって発生する第1ステップでの剛性変更などには注意してください。
接線勾配
指定した位置(荷重ステップ間は線形補間)とその直前のポイント(荷重ステップ)を結ぶ勾配とします。
等価せん断型モデル・等価曲げせん断型モデル
地震時の構造物の変形は、せん断的な変形(下左図)と曲げ的な変形(下右図)の組み合わさったものであると考えることができます。本プログラムでは、「等価せん断型モデル(全て非線形のせん断型成分であると仮定するモデル)」と、「等価曲げせん断型モデル(弾性の曲げ成分と非線形のせん断成分の組み合わせであると仮定するモデル)」の2つの考え方によるモデル化を行うことができます。
節点の鉛直変位から曲げ剛性を計算(曲げ剛性の直接入力では入力値を使用)し、曲げ変形成分を計算し、これを全体の層間変位から差し引いた残りをせん断変形成分とします。
ここで、
$K_1$:初期剛性
$α_2$・ $K_1$:第2剛性
$α_3$・ $K_1$:第3剛性
$Q_1,δ_1$:第1折点のせん断力,変位
$Q_2$, $δ_2$:第2折点のせん断力,変位
$Q_3$, $δ_3$:第3折点のせん断力,変位
本プログラムでは、第1折点および第3折点を指定し、第2折点を自動計算する方法(ルール1、2)と、第2折点および第3折点を指定し第1点を自動計算する方法(ルール3)があります。
ルール1、2による自動計算では、第3折点までの包絡面積がスケルトンカーブの包絡面積と等しくなるように、第2折点を設定します。また、第3勾配は第3折点の接線勾配とします。
ルール1では、第1折点はQ-δ曲線において割線剛性が初期剛性に対して指定値以下となった時点の変位により第1折点を決定します。
ルール2では、各階において最初に降伏部材が発生した時点の変位に対する比率を指定します。指定値に相当する変位を超えた時点の変位により第1折点を決定します。
ルール3による自動計算では、第2折点までの包絡面積がスケルトンカーブの包絡面積と等しくなるように、第1折点を設定します。また、第3勾配は第3折点の接線勾配とします。降伏ヒンジが発生した大梁端部の比率が指定値を超えた時点の変位により第2折点を決定します。
等価曲げ剛性の計算方法
第1ステップに関する柱の鉛直方向変位と柱軸力からひずみエネルギーの和が等しくなるような平面保持型の $_eθ_i$を求め、これに対応する等価曲げ剛性 $_eEI_i$を計算します。
i階での増分回転角を $_eθ_i$とすると、下式が成立するものとします。
$$ \sum_{j=1}^{n} \left( {}_{j}N_i・{}_j \Delta V_{i} \right) = \sum_{j=1}^n \left( {}_jN_i\left({}_e \Delta \theta_i・{}_jL_i \right) \right) $$したがって、
$$ e\Delta \theta_i = \frac{\sum_{j=1}^{n} N_i (_{j}N_i \cdot _j\Delta V_i )}{\sum_{j=1}^{n} (_{j}N_i \cdot _jL_{i} )} $$ここで、
$_jN_i$ : i階j軸の鉛直部材(柱、ブレース、壁、支持バネ)軸力 ※ブレースは指定により除外可。
$_jΔV_i$ : i層j軸の柱の鉛直方向変形
$_jL_i$ : i階j軸の柱の中立軸位置からの距離
等価曲げ剛性 $_eEI_i$は、モールの定理より
${}_e \Delta \theta _i = \int _{xi}^{xi+1} \frac{M_x}{EI_x} dx$したがって、等価曲げ剛性 $_eEI_i$は次式で求められます。
$e EI_i = h_i \frac{M_{i+1}+M_i}{2・{}_e \Delta \theta _i}$曲げ変形成分 $_bδ_i$は、下式で求められます。
$b \delta_i = {h_i}^2 \frac{2 \cdot M_i+M_{i+1}}{6 \cdot {}_e EI_i}$せん断変形成分 $_Sδ_i$は、下式で求められます( $δ_i$はi層の全体変形)。
${}_S \delta _i = \delta _i - {}_b \delta _i - \sum _{j=1}^{i-1} h_i・{}_e \Delta \theta _j$よって等価せん断剛性は次式で求められます。
${}_eGA_i = Q_i・\frac{h_i}{{}_s \delta _i}$中立軸位置の自動計算方法
下図に示した各層軸力jNiを用いて、軸力分布回帰直線の回転角と中立軸位置を求めています。
下式が最小となる直線を最小二乗法によって求め、軸力分布回帰直線としています。
$$ \sum _{j=1}^n \left({}_jN_i-{}_jL_i \cdot _{en}\theta _i \right)^2 $$ここで、
$_jN_i$ : i層j軸の鉛直部材(柱、ブレース、壁、支持バネ)軸力
$_jL_i$ : i層j軸の柱の中立軸位置からの距離
P-δ効果の評価方法(免震支承材)
鉛直支持材(柱・ブレース・壁など)の瞬間鉛直支持軸力と、各位置での瞬間層間変位を乗じて、P-δ効果による瞬間付加モーメント( $⊿M$)を算出します。指定されたフレームに含まれる全ての鉛直支持材についての瞬間付加モーメントの総和( $Σ⊿M$)を求め、Σ⊿Mを階高( $h$)で除して求めた層せん断力( $⊿Q$)をP-δ効果による層せん断力の低下とします。 $⊿Q$の計算は、Q-δ曲線の全ステップ分を逐次計算します。下図に示した各層軸力 $_jN_i$を用いて、軸力分布回帰直線の回転角と中立軸位置を求めています。免震支承材の場合、三山モデルを採用します。
$⊿M=P×δ$
$⊿Q=(Σ⊿M)/h$
質点系解析モデル
共通条件
X,Y方向別々のモデルとしてモデル化されます。
上下方向の自由度は拘束します。
剛性マトリクス
スウェイ・ロッキングを考慮した剛性マトリクスは、以下のように表されます。
ここで、
$[S]$:剛性マトリクス
$k_{ji}$:上部構造の剛性マトリクスの要素
$k_s$:スウェイのバネ定数
$k_R$:ロッキングのバネ定数
質量マトリクス
スウェイ・ロッキングを考慮した質量マトリクスは、以下のように表されます。
ここで、 $[M]$:質量マトリクス
$m_i$:i層の質量
$m_s$:基礎の質量
$m_r$:ロッキング質量慣性モーメント
$h_i$:i層の基礎からの高さ
モデル化タイプ
モデル化タイプは下記の3つから選択可能です。
等価せん断型
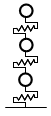
曲げ剛性を剛とします。(曲げ変形0)
剛床内並列ばねが設定できます。
一般的に塔状比の小さい建物で適用します。塔状比が大きい建物に適用した場合、立体モデルと高次モードの性状に差が生じてきます。
等価曲げせん断型
曲げ剛性を梁要素として考慮します。
剛床内並列ばねが設定できます。(Ver.2.8.0.4~)
一般的に塔状比の大きい建物で適用します。
速度依存ダンパーは曲げ変形を含んだ変形に対して作用します。
曲げせん断分離型
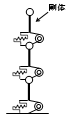
曲げ剛性を回転ばねとして考慮します。
剛床内並列ばねが設定できます。
一般的に塔状比の大きい建物で適用します。
モデル化が異なるため、等価曲げせん断型と固有周期に若干差が生じます。(概ね1%程度)
速度依存ダンパーをせん断変形のみに作用させることができます。
ダンパーのモデル化
ダンパーは履歴型、速度依存型によってそれぞれ下記のように選択できます。
履歴型ダンパーの場合
1.ダンパーを個別にモデル化する場合(付加ばねを介して質点間に接続)
各層ごとの保有付加剛性を設定するか、状態N,R,T解析から算出される保有付加剛性をダンパーごとに接続する方法があります。計算方法は保有付加剛性の計算方法をご参照ください。
2.Q-δ曲線上で分離する場合(直接質点間に接続)
静的荷重増分解析結果を元に、各ステップにおいて 各階ダンパー負担せん断力-各階層間変位関係を取得します。
この層せん断力-変形関係を元に、ダンパー部の骨格曲線をトリリニアとしてモデル化します。
速度依存型ダンパーの場合
1.保有付加剛性を考慮する場合(付加ばねを介して質点間に接続)
履歴型ダンパーと同様です。
※付加ばねに曲げ変形分が考慮されていると考え、減衰要素は付加ばねを介して質点間に配置します。
2.保有付加剛性を考慮しない場合(直接質点間に接続)
※曲げせん断分離型の場合、減衰要素はせん断変形にのみ作用します。
保有付加剛性の計算方法
各階ごとの保有付加剛性を算出する場合
各層保有付加剛性は以下の計算により算出します。
$K'_i = Q_i * (1 / \delta_R - 1 / \delta_N)$ダンパーごとの保有付加剛性を算出する場合
状態RまたはT解析によるダンパーの有効剛性に対し、状態Nによる実効変形比を考慮して付加剛性を算出します。
スウェイ・ロッキングモデル
質点系解析モデルは、層・階で認識される上部構造と、その下の基礎構造により構成されます。解析モデルは、層ごとに水平方向の振動自由度をもち、基礎はロッキング(基礎回転)とスウェイ(基礎移動)の2自由度を考慮できます。
上部構造の非線形特性は、増分解析結果からモデル化した復元力特性により評価します。基礎構造については、ロッキング・スウェイを入力値(ロッキング用重量慣性モーメント・ロッキングのバネ定数・ロッキングの減衰定数、スウェイ用重量・スウェイのバネ定数・スウェイの減衰係数)により評価します。
免震考慮モデル(免震層ねじれ考慮無し)の場合
免震考慮モデル(免震層ねじれ考慮無し)の場合は免震層については上部構造と同一のXY座標に対して集中配置されます(Ver.2.8.0.0よりモデル化を変更しました)。免震層の曲げ剛性は、上部構造の曲げせん断型の曲げ剛性と同様の方法で計算して考慮されます。上部構造については耐震モデルと同様にモデル化されます。免震層上下節点の自由度は並進方向、X軸回りおよびY軸回り回転をフリーとし、鉛直および回転自由度は拘束します。本モデルの場合は、スウェイ・ロッキングを考慮することができます。
免震考慮モデル(免震層ねじれ考慮、上部ねじれ非考慮)の場合
免震考慮モデル(免震層ねじれ考慮、上部ねじれ非考慮)の場合は免震層については立体的に配置され、上部構造については串団子モデルとしてモデル化されます。免震層上下節点の自由度は並進方向およびねじれ方向をフリーとし、X軸回りおよびY軸回りの回転自由度は拘束します。上部構造の各質点には並進質量の他に回転慣性質量が考慮されます。上部構造のねじれ剛性は剛としてモデル化します。本モデルで免震層のねじれの検討を行う際には以下の点に注意が必要です。
・質点系モデルを配置する座標を適切に設定する必要があります。免震層の一つ上の階のせん断力重心(軸力重心)に配置するのが望ましいです。
・本モデルでは免震層のねじれは精度よくモデル化できる可能性がありますが、上部構造の応答評価には適切でない場合があります。串団子モデルは原則的にねじれが生じない建物に対して行うモデル化であり、上部構造にねじれが生じる場合にはそのままでは精度よくモデル化できないことがあります。
・本モデルの場合は、スウェイ・ロッキングを考慮することができません。
固有値解析
固有値解析
固有値解析の解法
非減衰自由振動方程式
$$ [M]\{\ddot{x}\} + [S]\{x\} = 0 $$ここで、
$[M]$:質量マトリクス
$[S]$:剛性マトリクス
$\{x\}$:変位ベクトル
$\{\ddot{x}\}$:加速度ベクトル
は次式のような固有周期問題となります。
$$ \lambda\{V\} = [M]^{-1} [S]\{V\} $$このとき、 $[M]^{-1} [S]$は一般に対称行列ではなく、ロッキングを考慮した場合、 $[M]$
も対角行列とならないことから、以下に示すような対称行列の固有値問題に置換えて解きます。
まず、 $[M]$をコレスキーの平方根により、2つの三角行列の積で表します。
$$ [M] = [T] \times [T]^T $$ここで、 $[T]$は下半分の三角行列です。式(3)を式(2)に代入し、左から $[T]^T$を乗ずると、
$$ \lambda [T]^T \{V\} = \left( [T]^{-1} [S] \left[T^{-1}\right]^T \right) [T]^T \{V\} $$となります。従って、 $([T]^{-1}[S][T^{-1}]^T)$ の固有値、固有ベクトルを求めれば、式(4)の固有値、固有ベクトルおよび固有周期Tは次のように求まります。
$\lambda = \lambda^* \\ \{V\} = \left[T^{-1}\right]^T\{V^*\} \\ T = 2\pi/\sqrt{\lambda}$なお、 $([T]^{-1}[S][T^{-1}]^T)$ の固有値解析は、振動自由度がに300以下の場合はヤコビ法により、300を超える場合はサブスペース法により計算されます。
刺激係数
式(1)に外乱として地震力を考慮すると
$[M]\ddot{x}+[S]x = -[M]\ddot{z}$ (6)
ここで、 $\ddot{z}$:地震加速度
$\{x\} = [V]\{q\}$とおき、左から $[V]$を乗ずれば、式(7)のようにモード分解することができます。
$\{\ddot{q}\} + [A]\{q\} = \{p\}$ (7)
ここで、
$[A] = ([V]^T[M][V])^{-1}[V]^T[S][V]$$\{p\}$ = $-([V]^T[M][V])^{-1} \times [V]^T[M]\{\ddot{z}\}$ = $-\{\ddot{z}\} \times \{ \beta \}$
$\{\beta\}$を刺激係数と呼び、ロッキング・スウェイを考慮した場合の式で表せば次のようになります。
$\{ \beta \} = -([V]^T[M][V])^{-1}[V]^T[M]\{I\}$ (8)
ここで、
減衰マトリクス
減衰マトリクス
減衰タイプ
本プログラムでは減衰タイプを剛性比例型もしくはレーリー減衰およびモード別減衰から選択できます。剛性比例型とした場合、入力値された「 $T_i$(減衰指定固有周期)」、「 $h_i$(減衰定数)」から、下式により各部の減衰係数を計算します。
$C_i = \frac{T_i \times h_i}{\pi} \times S_i$減衰マトリクス $[C]$の作成は、剛性マトリクス $[S]$に準じます。また、剛性変更に伴う減衰項の変更を指定することができます。
剛性変更に伴う減衰項の変更
剛性変更に伴う減衰項の変更を指定できます(操作編マニュアル参照)。
- 初期剛性比例減衰
初期剛性に対する減衰マトリクス $[C]$を用います。
- α1一定
初期剛性に対する $\alpha_1$、瞬間剛性マトリクス $[S]$より、以下とします。
$[C] = \alpha _1 [S]$- h1一定
瞬間剛性に対する1次の固有円振動数 $\omega_1$を以下と仮定します。
$\omega _1 = \omega _{1e} \times \sqrt {\frac{\{u\}^T[S]\{u\}}{\{u\}^T[S_e]\{u\}}}$指定された $h_1$より、瞬間減衰マトリクス $[C]$を定義します。
$[C] = \frac{2h_1}{\omega _1} [S]$ここで、 $[C]$:瞬間減衰マトリクス
$[S]$:瞬間剛性マトリクス
$[S_e]$:初期剛性マトリクス
$h_1$:(1次の)減衰定数(入力値)
$\omega _{1e}$:初期剛性による1次の固有円振動数(減衰指定固有周期の入力がある場合は、入力値の固有周期から求まる1次の固有円振動数)
$\{u\}$:初期剛性による1次の固有ベクトル
累積型・非累積型
累積型は、増分減衰力を積分することにより減衰を評価します。 非累積型は、減衰力を瞬間減衰マトリクス×速度 として求めます。
ここで、
$[C]$ :瞬間減衰マトリクス
$\{ \Delta \dot x\}$:増分速度
$\{ \dot x\}$:速度
振動解析の解法
振動解析の解法
振動方程式は直接積分法により、次式で解きます。
$[M]\{\ddot{x}_n\} + \{C_n\} +\{F_n\} = \{f_n\}$時刻ステップnでの変位、復元力、減衰力を以下の式で表します。
$\{x_n\} = \{x_{n-1}\} + \{ \Delta x_n\}$ $\{F_n\} = \{F_{n-1}\} + [S_n]\{ \Delta x_n\}$ $\{C_n\} = \{C_{n-1}\} + [C_n]\{ \Delta \dot x_n\}$ここで、
$[S_n]$:時刻ステップnでの瞬間剛性マトリクス
$[C_n]$:時刻ステップnでの瞬間減衰マトリクス
弾塑性振動方程式は、以下となります。
$[M]\{\ddot x_n\} + [C_n]\{ \Delta \dot x_n\} + [S_n]\{ \Delta x_n\} + \{C_{n-1}\} + \{F_{n-1}\} = \{f_n\}$加速度を増分形で表すと、下式になります。
$\{ \ddot x_n\} = \{ \ddot x_{n-1}\} + \{ \Delta \ddot x_{n}\}$これを振動方程式に代入して、以下の式を得ます。
$[M]\{ \Delta \ddot x_{n}\} + [C_n]\{ \Delta \dot x_{n}\} +[S_n]\{ \Delta x_{n}\} + [M]\{ \ddot x_{n-1}\} + \{C_{n-1}\} + \{F_{n-1}\} = \{f\}$上式を、ニューマークβ法により直接解きます。すなわち、時刻ステップnの変位、速度は次式により表されます。
$x_n = x_{n-1} + \Delta t \Delta \dot x_{n-1} + \frac{ \Delta t^2}{2}x_{n-1} + \beta \Delta t ^2(\ddot x_n - \ddot x_{n-1})$ $\dot x_n = \dot x_{n-1} + \Delta t \Delta \ddot x_{n-1} + \frac{\Delta t}{2}(\ddot x_n - \ddot x_{n-1})$ここで、 $\Delta t$:時間刻み
これを増分形で表すと、以下のようになります。
$\{ \Delta x_n\} = \{x_n\} -\{x_{n-1}\} = \Delta t \{ \dot x_{n-1}\} + \frac{\{\Delta t\}^2}{2}\{\ddot x_{n-1}\} + \beta\{\Delta t\}^2\{\Delta \ddot x_n\}$ ${ \Delta \ddot x_n} = { \dot x_n} - { \dot x_{n-1}} = \Delta t {\ddot x_{n-1}} + \frac{\Delta t}{2}{\ddot x_n}$これらを用いて、 ${\Delta t}$について整理すると、次式が得られます。
${ \Delta \ddot x_n} = \{ [M] + \frac{\Delta t}{2}[C_n] + \beta{\Delta t}^2[S_n] \}^{-1} ・ [{ f_n - {[M] + \Delta t[C_n] + \frac{{\Delta t}^2}{2}[S_n] } {\ddot x_{n-1}} - \Delta t[S_n]{ \dot x_{n-1}} -{C_{n-1}} - {F_{n-1}} }]$免震支承材
免震支承材
免震支承材の履歴特性
鉛プラグ挿入型積層ゴム
a) LRB統一型
複数メーカーの統一仕様による「歪依存型バイリニア特性」です。
鉛プラグ入り積層ゴム概略図
(1) 二次剛性 $K_d(γ)$(kN/cm)
$K_d (\gamma) = C_{Kd}・K_d$ $K_d = ( K_r + K_p )$$K_r$ :積層ゴムの水平ばね定数
$K_r = G_r \frac{A_r}{H}$$G_r$:ゴムのせん断弾性率
$A_r$ :積層ゴムの断面積
$H$:ゴム総厚
$K_p$ :鉛プラグによる水平剛性増加分
$K_p = α_p \frac{A_p}{H}$$α_p$:鉛の見掛けのせん断弾性係数
$A_p$:鉛プラグ断面積
$C_{Kd}$:降伏後剛性のひずみ依存による修正係数
$$ C_{Kd} = \begin{cases} 0.779γ^{0.41} &(γ<0.25) \\\\\\ γ^{-0.25} &(0.25≤γ<1.0) \\\\\\ γ^{-0.12} &(1.0≤γ<2.5) \end{cases} $$$γ$:歪
(注) $G_r,α_p$については次項の付表-1 を参照してください。
(2) 切片荷重 $Q_d(γ)$
$Q_d(\gamma) = C_{Qd}・Q_d$ $Q_d = \sigma _{pb}・A_p$$σ_{pb}$:鉛の降伏せん断応力度(kN/cm2)
$C_{Qd}$:降伏荷重のひずみ依存による修正係数
$$C_{Qd} = \begin{cases} 2.036γ^{0.41} & (γ≤0.1) \\\\\\ 1.106γ^{0.145} & (0.1<γ<0.5) \\\\\\ 1 & (0.5≤γ) \end{cases}$$γ:歪
(注) $σ_{pb}$については次項の付表-1 を参照してください。
(3) 初期剛性 $K_u$
$K_u = \beta・K_d$β:初期剛性の二次剛性に対する倍率
β=10~15とし、G4はβ=13、G6はβ=10を推奨
(4) 等価水平剛性 keq
$k_{eq} = \frac{Q_d}{γ・H} + K_d$(5) 等価粘性減衰定数 $H_{eq}$
$H_{eq}=\frac{2}{π} \cdot \frac{{Q} _{d} \lbrace \gamma \cdot H-\frac{{Q} _{d}}{{(β-1)K} _{d}} \rbrace }{{k} _{eq} \cdot (γ \cdot H)^2}$(6) 補正後の降伏後剛性 $K'_d$および降伏荷重 $Q'_d$
$K'_d = {\alpha} _{Kd}・{K} _{d}$ $Q'_d = {\alpha} _{Qd}・{Q} _{d}$$α_{Kd}:K_d$の補正係数
$α_{Qd}:Q_d$の補正係数
ここで、温度依存性について、温度 $t_0$への換算式は次式とします。
$K_d(t_o) = K_d(20)・exp(-0.00271(t_o-20)$ $Q_d(t_o) = Q_d(20)・exp(-0.00879(t_o-20)$b) オイレス工業歪み依存Tri-Linear型
オイレス工業鉛プラグ挿入型積層ゴム支承の「歪み依存トリリニア特性」です。
ここで、
$K_d$ :降伏剛性(kN/m)
$K_d = 0.779・\gamma^{-0.43} ・K_{d100}$[γ<0.25]
$K_d = \gamma^{-0.25}・K_{d100}$[0.25≦γ<1.0]
$K_d = \gamma^{-0.12}・K_{d100}$[1.0≦γ<2.5]
$K_{d100}$:せん断ひずみγ=100%時の降伏後剛性
$K_1$ :第1剛性
$K_1 = \beta _1・K_d$$\beta _1 = K_1/K_d$(推奨値:45)
$K_2$ :第2剛性
$K_2 = \beta _2・K_d$$\beta _2 = K_2/K_d$(推奨値:2.5)
$Q_d$ :降伏荷重
$Q_d = 2.036・ \gamma ^{0.41}・Q_{d100}$[γ≦0.1]
$Q_d = 1.106・ \gamma ^{0.145}・Q_{d100}$[0.1<γ<0.5]
$Q_d = Q_{d100}$[0.5≦γ]
$Q_{d100}$:せん断ひずみ $γ=100%$時の降伏荷重
$Q_{y1}$ :第1折れ点荷重
$α_1$ : $Q_{y1}/Q_d$(推奨値:0.7)
復元力特性タイプ(=135)を指定されたバネについては、応答計算に入る時に初期剛性を再計算します。
初期剛性は歪が0.05 における $K_1$とし、以降下記の規則に従って弾塑性の判定が行われます。
① |γ|≦0.05 の範囲においては、γ=0.05 として式1、式4、式5により求まるトリリニアルールに従って動きます。
② |γ|>0.05 の範囲におけるスケルトン上の動きは式1、式2または式3で求まる $K_d$を瞬間剛性とします。
③ スケルトンからの除荷時において、式1~3、式4および式5~7によりトリリニアルールを設定します。
④ トリリニアループから最大変形をこえると、スケルトン上に戻ります。
以降、②、③を繰り返します。
c) オイレス工業修正H-D型
オイレス工業鉛プラグ挿入型積層ゴム支承の「歪み依存修正H-D特性」です。
弾性すべり支承
すべり支承履歴特性は摩擦ばね要素による標準型バイリニアとします。
滑っている状態ではばね剛性は作用しないため、完全バイリニア型になります。
ブリヂストン製の装置の場合、ユーザー指定により速度を直接指定して摩擦係数を変更することが可能です。速度を指定した場合、下記の計算により摩擦係数を設定します。
(SPシリーズ) $\mu = 0.0424 \sigma^{-0.510} V^{0.0894}$ (σ=18N/mm2、V:速度mm/s)
(SLシリーズ) $\mu = (0.112-0.00276 \sigma) V^{0.0863}$ (σ=10N/mm2、V:速度mm/s)
(SKシリーズ) $\mu = (\sigma/18)^{-0.51} \times (0.0073V^{0.0894})$ (σ=18N/mm2、V:速度mm/s)
高減衰ゴム系積層ゴム
ブリヂストン
ブリヂストン高減衰積層ゴムです。各タイプの係数は以下の通りです。
・E6タイプ
$Geq$ : $2.309 - 4.327 \gamma + 4.456 \gamma ^2 - 2.379 \gamma ^3 + 0.630 \gamma ^4 - 0.0649 \gamma ^5$
$Heq$ : $0.1894 + 0.0664 \gamma - 0.0353 \gamma ^2 + 0.0041 \gamma ^3$
$U$ : $0.3726 + 0.0956 \gamma - 0.0741 \gamma ^2 + 0.0113 \gamma ^3$
・E4タイプ
$Geq$ : $1.308 - 2.438 \gamma + 2.640 \gamma ^2 - 1.483 \gamma ^3 + 0.4086 \gamma ^4 - 0.043 \gamma ^5$
$Heq$ : $0.227 + 0.0120 \gamma - 0.0088 \gamma ^2 + 0.0037 \gamma ^3$
$U$ : $0.379 + 0.0069 \gamma - 0.0046 \gamma ^2 + 0.0026 \gamma ^3$
・X6Rタイプ
$Geq$ : $G_0 \times (2.855 - 3.878 \gamma + 2.903 \gamma ^2 - 1.016 \gamma ^3 + 0.1364 \gamma ^4)$
$Heq$ : $H_{eq0} \times (0.9150 + 0.2364 \gamma - 0.1804 \gamma ^2 + 0.02902 \gamma ^3)$
$U$ : $u_0 \times (0.9028 + 0.2711 \gamma - 0.2083 \gamma ^2 + 0.03421 \gamma ^3)$
$G_0$ = $0.620$、 $H_{eq0}=0.240、u_0=0.408$
・X4Rタイプ
$Geq$ : $1.145 - 1.583 \gamma + 1.192 \gamma ^2 - 0.416 \gamma ^3 + 0.054 \gamma ^4$
$Heq$ : $0.216 - 0.008 \gamma + 0.018 \gamma ^2 - 0.006 \gamma ^3$
$U$ : $0.3617 - 0.0132 \gamma + 0.0325 \gamma ^2 - 0.0110 \gamma ^3$
・X3Rタイプ
$Geq$ : $0.8703 - 1.1028 \gamma + 0.7283 \gamma ^2 - 0.2213 \gamma ^3 + 0.0255 \gamma ^4$
$Heq$ : $0.166 - 0.006 \gamma + 0.015 \gamma ^2 - 0.005 \gamma ^3$
$U$ : $0.2720 - 0.0105 \gamma + 0.0262 \gamma ^2 - 0.0087 \gamma ^3$
・X4Sタイプ
$Geq$ : $1.145 - 1.583 \gamma + 1.192 \gamma ^2 - 0.416 \gamma ^3 + 0.054 \gamma ^4$
$Heq$ : $0.236 - 0.009 \gamma + 0.020 \gamma ^2 - 0.007 \gamma ^3$
$U$ : $0.4001 - 0.0190 \gamma + 0.0401 \gamma ^2 - 0.0132 \gamma ^3$
東洋ゴム
東洋ゴム高減衰積層ゴムです。
HRBおよびSHRBが選択可能です。
SHRB-E4タイプおよびSHRB-E6タイプはブリヂストン高減衰ゴムと同様の計算を行います。
鉄粉・ゴム混合材プラグ挿入型積層ゴム(ブリヂストン)
鉄粉・ゴム混合材プラグ挿入型積層ゴム(eRB)は歪依存バイリニア型です。各係数は以下の通りです。
・G0.4タイプ
$Ckd$ : $1.481 - 0.6781 \gamma + 0.2166 \gamma ^2 - 0.01958 \gamma ^3$
$Cqd$ : $0.2036 + 0.8047 \gamma + 0.1172 \gamma ^2 - 0.1505 \gamma ^3 - 0.02502 \gamma ^4$
鉄粉・ゴム混合材プラグ挿入型積層ゴムは下記が選択できます。
・旧認定(ゴム径・プラグ径による低減無し)
・現認定MVBR-0508(プラグ径の関数による低減を考慮)
現認定 MVBR-0508を選択した場合は下記式で二次剛性、切片荷重の低減を考慮します。
| No. | 項目 | 基準値 |
|---|---|---|
| 1. | 二次剛性 | $K_d=D_{Kd}(D_p)×(G_r×A_r/H_r+α_p/H_r)$ $D_{Kd}(D_p)$:下式にて与えられるプラグ径 $D_p$に対する $K_d$の依存式 $D_{Kd}$ = $1 (D_p≦180)$ $-2.161×10-^3(D_p-180)+1(180<D_p)$ $α_p$:ひずみ100%時におけるプラグの見かけのせん断弾性率(4.7N/mm2) |
| 2. | 切片荷重 | $Q_d$ =
$D_{Qd}(D_p)×τ_p×A_p$ $D_{Qd}(Dp)$:下式にて与えられるプラグ径 $D_p$に対する $Q_d$の依存式 $D_{Qd} = 1 (D_p≦200)$ $-4.279×10-^3(D_p-200)+1 (200<D_p)$ $τ_p$:ひずみ100%時のプラグの降伏応力(6.446N/mm2) |
$A_r$: ゴム部分の断面積(mm2)
$H_r$: ゴム総厚(mm)
$A_p$: プラグ面積(mm2)
$G_r$: ひずみ100%時におけるゴムのせん断弾性率(0.385N/mm2)
U型ダンパー
標準バイリニア型でモデル化します。
積層ゴム一体型U型ダンパーとして配置した場合、並列して天然ゴム系積層ゴムが配置されます。
錫プラグ挿入型積層ゴム
錫プラグ挿入型積層ゴム免震部材のモデル化です。
a) 歪み依存Bi-Linear
錫プラグ入積層ゴム 復元力特性モデル(歪依存型バイリニアモデル)
(1) 二次剛性 $K_2$
$K_2 = \frac{G \cdot A_r}{n \cdot t_r}$$G$ :ゴム材料のせん断弾性率
$A_r$ :ゴムの受圧面積
$n$ :ゴム層数
$t_r$ :ゴム1 層厚さ
$K_2(\gamma) = (0.997 \times \gamma^{-0.403})K_2( \gamma _{100})$(γ<1.0)
$K_2(\gamma) = (1.0 + (-0.313)In(\gamma)) K_2( \gamma _{100})$ (γ≧1.0)
$γ$ :ひずみ
$γ_{100}$ :ひずみ100%
(2) 切片荷重 $Q_d$
$Q_d = A_p・\tau _d$(kN)
$A_p$ :錫プラグ断面積 (cm2)
$τ_d$ :錫プラグ降伏応力度 (kN/cm2)
$Q_d(\gamma) = (1.0 + 0.013In(\gamma))Q_d(\gamma _{100})$(γ<1.0)
$Q_d(\gamma) = (1.0 + (-0.079)In(\gamma))Q_d(\gamma _{100})$(γ≧1.0)
b) 歪み依存Tri-Linear
(1) せん断歪み100%時降伏後剛性 $K_{p100}$
$K_{p100} = \frac{G \cdot A_r}{n \cdot t_r}$$G$ :ゴム材料のせん断弾性率
$A_r$ :ゴムの受圧面積
$n$ :ゴム層数
$t_r$ :ゴム1 層厚さ
$K_p(\gamma) = (0.997 \times \gamma^{-0.403})・K_{p100})$(γ<1.0)
$K_p(\gamma) = (1.0 + (-0.313)In(\gamma))・K_{p100}$(γ≧1.0)
$γ$ :ひずみ
$γ_{100}$ :ひずみ100%
(2) せん断歪100%時の切片荷重 $Q_{d100}$
$Q_{d100} = A_p・\sigma _d$(kN)
$A_p$ :錫プラグ断面積 (cm2)
$σ_d$ :せん断歪み100%時錫プラグ降伏応力度 (kN/cm2)
$Q(\gamma) = (1.0 + 0.013In(\gamma))Q_{d100}$(γ<1.0)
$Q(\gamma) = (1.0 + (-0.079)In(\gamma))Q_{d100}$(γ≧1.0)
転がり支承
履歴特性は標準型バイリニアとします。
折れ点耐力は軸力一定を仮定し、長期軸力と摩擦係数から計算します。第2剛性倍率は1/10000とします。また、摩擦係数μは下記により計算します。
$Q1 = \mu・P_V$ $\mu = (1.2+7.8 \times P_V/ P_o)/1000$$Pv$ :長期軸力
$Po$ :静定格圧縮荷重
また、初期剛性は変形が0.2mmに達するまで維持するものと仮定して復元力特性を設定します。
鉛ダンパー
標準バイリニア型でモデル化します。
球面すべり支承
球面すべり支承の計算モデルでは時々刻々の支承材に生じる速度によって以下の式により摩擦係数が計算されます。
$\mu = \mu _0・(1.0 - 0.55・e^{-0.019・|V|})$(MNタイプ)
$\mu = \mu _0・(1.03 - 0.55・1.5^{-0.018・|V|})$(LNタイプ)
$μ$:すべり摩擦係数 $μ_0$:標準摩擦係数 $V$:層間速度(mm/s)
標準摩擦係数 $μ_0$の面圧依存性は以下の計算式により算出して考慮します。
(MNタイプ)
$μ_0$ = (基準摩擦係数 0.043)×(面圧補正係数)
(面圧補正係数) = 2.03×σ-0.19+0.068
(LNタイプ)
$μ_0$ = (基準摩擦係数 0.013)×(面圧補正係数)
(面圧補正係数) $= 20×σ-0.9+0.5$
σ :長期支持荷重
◇補正係数の算出例(MNタイプの場合)
補正係数=(製造ばらつきの補正係数)×(気温の補正係数)×(繰り返しの補正係数)
ここで、
・製造ばらつきの補正係数
製造による摩擦係数のばらつきの絶対値は、基準摩擦係数0.043(基準温度、基準面圧)に対して±0.01としています*注1。したがって、
製造ばらつきの補正係数+側最大: $(0.043+0.01)/0.043=1.233$
製造ばらつきの補正係数-側最大: $(0.043-0.01)/0.043=0.767$
となります。
・気温の補正係数
摩擦係数の気温に対する依存性は、基準温度20℃の時の標準摩擦係数に対する比として以下のような依存式として表されます。
気温の補正係数:温度依存式 $y=1.258 × exp(-0.011 × T)$
T :想定する環境温度(℃)
ここで、気温の補正係数が+側になるのは低温時、-側になるのは高温時です。
例えば、
0℃ (温度が低い側)の場合の気温の補正係数:1.258
30℃(温度が高い側)の場合の気温の補正係数:0.904
となります。
・繰り返しの補正係数
繰り返し変形によって生じるすべり面の温度上昇による摩擦係数への影響は、基準温度20℃の時の標準摩擦係数に対する比として以下のように考えています。
繰り返しの補正係数:
補正係数の+側、-側とも、繰り返しによる温度上昇により0.8
以上のことから、補正係数の+側は、
(製造ばらつきの補正係数+側最大)×(温度が低い場合の気温の補正係数)×(繰り返しによる補正係数0.8)
補正係数の-側は、
(製造ばらつきの補正係数-側最大)×(温度が高い場合の気温の補正係数)×(繰り返しによる補正係数0.8)
となります。
例えば、補正係数の+側は、低温側の環境温度を10℃と想定する場合、製造のばらつき1.213、気温の補正係数1.258、繰り返しによる補正係数0.8 を掛け合わせ、1.221 となります。
同様に、補正係数の-側は、高温側の環境温度を30℃と想定する場合、製造のばらつき0.787、気温の補正係数0.904、繰り返しによる補正係数0.8 を掛け合わせ、0.569 となります。
*注:直近の摩擦係数のばらつきについては、メーカーにお問い合わせ下さい。
筒状流体・粘性体ダンパーの部材モデル
筒状流体・粘性体ダンパーの部材モデル
筒状流体・粘性体ダンパーは剛域付きのダンパー要素でモデル化されます。ダンパーに発生する減衰力に対し上部および下部節点が回転するモデル化となるため、上部節点および下部節点は回転に対して抵抗できる条件となっている必要があります。
下側節点が左端の場合 下側節点が右端の場合
例えば下記の配置では回転に対して抵抗できず、ダンパーは減衰力を負担できませんのでモデル化を変更する必要があります。
長周期地震動に対する繰り返し依存性
長周期地震動に対する繰り返し依存性
オイレス工業鉛プラグ挿入型積層ゴム
オイレス工業の鉛プラグ挿入型積層ゴムにおいて繰り返し依存性を考慮する場合、以下の計算により繰り返し依存性が評価されます。性能更新のタイミングは除荷時になります。
切片荷重
$$Qd = Qd \cdot _{LRB}k_{min}$$
(1) 繰り返し低下率 $_{LRB}k_{min}$
$$ _{LRB} k _{min} = \frac{8.33}{7.97} × (-0.06 + 1.25 × exp(-\frac{f(D _{pb}}{360} × \frac {W _{pb}}{V _{pb}}))$$$f(D_{pb})$:鉛直径補正値(=1/6×Dpb0.3)
$W_p$:LRB総履歴吸収エネルギー
$V_{pb}$:鉛プラグ体積
(2) 鉛プラグ体積平均温度Tの算出
$$ _{LRB} k _{min} = \frac{327.5}{1.1T} × (1.16 - 1.25 × exp(-\frac{f(D _{pb}^{0.3})}{2160} × \frac {W _{pb}}{V _{pb}}))$$【ブリヂストン鉛プラグ挿入型積層ゴム】
ブリヂストンの鉛プラグ挿入型積層ゴムにおいて繰り返し依存性を考慮する場合、以下の計算により繰り返し依存性が評価されます。性能更新のタイミングは除荷時になります。計算方法は評定書「BCJ評定-IB0012-01」(長周期地震動に対する免震材料の性能変化(ブリヂストン鉛プラグ入り積層型ゴム支承))に従います。
切片荷重: $$Q'_d = Q_d \cdot k$$
kは次式により計算されます。
$$k = \frac{8.33}{7.967} × (-0.06 - 1.25 \cdot exp(-\frac{E'}{360V_p}))$$
 :鉛プラグ単位面積当たりの代表累積吸収エネルギー量(MPa)
:鉛プラグ単位面積当たりの代表累積吸収エネルギー量(MPa)
鉛プラグ単位面積当たりの代表累積吸収エネルギー量は以下の式で計算されます。
$\frac{E'}{V_p} = γ \cdot \frac{E}{V_p}$またrは以下のように定義されます。
シングルプラグの場合
$$ \gamma = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle {0.001214D_p + 0.5698} & \left( D_p \leq 354 \right) \\ \displaystyle {1} & \left( 354 < D_p \right) \end{array} \right. \end{align}$$マルチプラグの場合
$$\gamma = 0.9277$$ここで
$D_p$:鉛プラグ径(mm)
ブリヂストン高減衰ゴム系積層ゴム支承
ブリヂストンの高減衰ゴム系積層ゴムにおいて繰り返し依存性を考慮する場合、以下の計算により繰り返し依存性が評価されます。性能更新のタイミングは除荷時になります。計算方法は評定書「BCJ評定-IB0010-01」(長周期地震動に対する免震材料の性能変化(ブリヂストン高減衰積層ゴム支承))に従います。
内部ゴムの代表温度Tと水平性能の関係式は支承材タイプごとに異なります。繰り返し変形による影響を補正する前の等価剛性( $K_{eq}$)、等価粘性減衰定数( $H_{eq}$)、降伏荷重特性値(u)と、繰り返し変形による影響を補正した後の等価剛性( $K'_{eq}$)、等価粘性減衰定数( $H'_{eq}$)、降伏荷重特性値(u’)の関係は以下の通りです。
a) X0.6Rタイプ
(1) 等価剛性:
$$K_{eq}' = C_k ・K_{eq}$$ $$C_k = \begin{cases} {1.288-0.0144T} (T≤20℃)\\\\\\ {1.668-0.548log(T-3.45)} (T>20℃) \end{cases}$$ここでlogは常用対数。
(2) 等価粘性減衰定数
$$H_{eq}' = C_h \cdot H_{eq}$$ $$C_h = -0.0065 + 1.130$$(3) 降伏荷重特性値
$$u' = C_u \cdot u$$ $$C_u = -0.0065T + 1.130$$b) X0.4S/X0.4Rタイプ
(1) 等価剛性:
$K_{eq}' = C_k ・K_{eq}$ $$C_k = \begin{cases} {1.735-0.0368T} (T≤20℃)\\\\\\ {1.272-0.402log(T-15.30)} (T>20℃) \end{cases}$$ここでlogは常用対数。
(2) 等価粘性減衰定数
$$H_{eq}' = C_h \cdot H_{eq}$$ $$C_h = -0.0010T + 1.020$$(3) 降伏荷重特性値
$$u' = C_u \cdot u$$ $$C_u = -0.0010T + 1.020$$c) X0.3Rタイプ
(1) 等価剛性:
$$K_{eq}' = C_k ・K_{eq}$$ $$C_k = \begin{cases} {1.523-0.0262T} (T≤20℃)\\\\\\ {1.228-0.317log(T-14.75)} (T>20℃) \end{cases}$$ここでlogは常用対数。
(2) 等価粘性減衰定数
$$H_{eq}' = C_h \cdot H_{eq}$$ $$C_h = -0.0013T + 1.026$$(3) 降伏荷重特性値
$$u' = C_u \cdot u$$ $$C_u = -0.0013T + 1.026$$内部ゴムの代表温度Tは以下の式により計算されます。
$$T = \begin{cases} {T_0 + \frac{E}{V_Rρ_Rc_R}} (E/V_R ≤ 10MPa)\\\\\\ {T_0 + \frac{10}{ρ_Rc_R} + \frac{E-10V_R}{V_Rρ_Rc_R + V_sρ_sc_s}} (T>20℃) \end{cases}$$T0:初期温度(℃)
$T_0$:内部ゴムの密度 (kg/mm^3)
$P_s$:内部鋼板の密度 (kg/mm^3)
$C_R$:内部ゴムの比熱 (ml/kg・K)
$C_S$:内部鋼板の比熱 (ml/kg・K)
$V_S$:内部鋼板の体積 (mm^3)
$V_s = \frac{π(D_o^2 - D_i^2)}{4} \times T_s(n-1)$$V_R$:内部ゴムの体積 (mm^3)
$E$:累積吸収エネルギー(mJ)
内部ゴム、内部鋼板の比熱、密度については下表に従うこととします。
| 対象 | 密度 $ρ_R$, $ρ_S$ (kg/mm3) | 比熱 $C_R$, $C_S$(mJ/kg・K) |
|---|---|---|
| 内部ゴム | 1.15 × 10-6 | 1.45 × 106 |
| 内部鋼板 | 7.85 × 10-6 | 5.02 × 105 |
制振要素
制振要素
減衰要素(非線形要素、マクスウェル要素)については求められた要素力を節点力として運動方程式に与えて解きます。したがって、運動方程式には減衰要素を構成するダンパーまたはバネは、減衰あるいは剛性マトリクスには加算されません。
マクスウェル要素
連結点でのバネとダンパーの力の釣合い条件と、連結点の変位と速度の関係を陽的に仮定します。求められた要素力を節点力として運動方程式に与えて解くものとします。
- 運動方程式
時刻 $t+\Delta t$での運動方程式を表すと、次式となります。ここで、マクスウェル要素の節点力を $M {}_F$とします。
$M ^{t+\Delta t}\ddot{U}$ + $C {} ^{t+\Delta t} \dot{U}$ + $K {} ^{t+\Delta t}U$ + ${} ^{t+\Delta t}{_mF}$ = ${} ^{t+\Delta t}R$
これを増分形で表すと、下式になります。
$M ^{t+\Delta t} \ddot{U}$ + $ ^tC \Delta \dot{U}$ + ${} ^tK{\Delta U}$ = ${} ^{t+\Delta t}R$ - $ _s^tF$ - $ _d^tF $ - $ ^{t+ \Delta t}F _m$ + $^{t+ \Delta t}R _{umb}$
上式の ${}^{t+\Delta t}R _{umb}$は不平衡力です。
- マクスウェル要素の計算
マクスウェル要素の相対変位と相対速度の関係は次式となります。
$U_{ij} = U_{i0} + U_{0j}$ $\dot{U_{ij}} = \dot{U_{i0}} + \dot{U_{j}}$ここで、
$U_{ij}$:
$i-j$の相対変位
$U_{i0}$: $i-0$の相対変位
$U_{0j}$: $0-j$の相対変位
$\dot{U_{ij}}$: $i-j$の相対速度
$\dot{U_{i0}}$: $i-0$の相対速度
$\dot{U_{0j}}$: $0-j$の相対速度
連結点0の力の釣合いは次式となります。バネ力を $F_k$、ダンパー力を $F_c$、マクスウェル要素力を $F_{ij}$とします。
$F_k = F_c = F_{ij}$バネ力は線形を仮定し、次式で定めます。ここで、バネの初期剛性を $K_d$とします。
$F_k = K_d (U_{ij} - U_{0j})$ダンパー力は非線形なので次式となります。 $C^{'}$は接線減衰係数となります。
ここで、 $Q_c$は以下とします。
$\dot{U_{0j}} > 0$は正側の切片の値
$\dot{U_{0j}} < 0$は負側の切片の値
よって、連結点の釣り合い条件は式7.6.1.5に式7.6.1.6、式7.6.1.7を代入し、次のようになります。
$K_d (U_{ij} - U_{0j}) = C^{'} \dot{U_{0j}} + Q_c$時間刻みが十分小さい場合、時刻の速度を-からまでの平均速度で近似すれば、時刻び速度は次式で表されます。
${}^t \dot{U_{0j}} = \frac{\Delta ^tU_{0j}}{\Delta t}$ここで、 ${}^t \dot{U_{0j}}$:時刻の0-jの相対速度
${}^t \dot{U_{0j}}$:時刻の0-jの相対変位の増分
$\Delta ^t \dot{U_{0j}}$:時刻刻み
代入すれば、次式のとなります。
$K_d(U_{ij} - U_{0j}) = C^{'} \frac{\Delta ^tU_{0j}}{\Delta t} + Q_c$また、時刻の相対変位を時刻-と増分の和で表すと、次式となります。
${}^tU_{0j} = {}^{t-\Delta t}U_{0j} + \Delta^tU_{0j}$上式を $\Delta \dot{U_{0j}}$についてまとめると、次式となります。
$K_d {}^tU_{ij} - K_d {}^tU_{0j} = C^{'} \frac{\Delta^tU_{0j}}{\Delta t} + Q_c$ $K_d {}^tU_{ij} - K_d ({}^{t-\Delta t}U_{0j} + \Delta^tU_{0j}) = C^{'} \frac{\Delta^tU_{0j}}{\Delta t} + Q_c$ $K_d ({}^{t-\Delta t}U_{0j} - \Delta^tU_{0j}) - K_d \Delta^tU_{0j} = C^{'} \frac{\Delta^tU_{0j}}{\Delta t} + Q_c$ $(\frac{C^{'}}{\Delta t} + K_d) \Delta^tU_{0j} = K_d ({}^t \Delta U_{ij} - {}^{t-\Delta t}U_{0j}) - Q_c$ $\therefore \Delta^tU_{0j} = \frac{K_d({}^tU_{ij} - {}^{t-\Delta t}U_{0j}) - Q_c}{C^{'}/\Delta t + K_d}$代入すれば ${}^tU_{0j}$が求まります。時刻 $t$の $0‐j$の相対速度についてまとめると、次式となります。
${}^tU_{0j} = \frac{K_d({}^tU_{ij} - {}^tU_{0j}) - Q_c}{C^{'}}$したがって、連結点0の変位 ${}^tU_0$と速度 ${}^t \dot{U_0}$は次式で求まります。
${}^tU_0 = {}^tU_j + {}^tU_{0j}$ ${}^t \dot{U_0} = {}^t \dot{U_j} + {}^t \dot{U_{0j}}$日鉄住金関西工業(株)SUB(Steel-Unbuckling-Brace/鋼製座屈拘束ブレース)
SUBの履歴特性は標準型とします。
各項目の詳細につきましては、日鉄住金関西工業(株)の技術資料をご参照ください。
a) SLY100
(1) 完全弾塑性モデル
$P$:第1折れ点耐力
$P = P_y・\phi$$P_y$:ブレースの降伏軸力
$P_y = Ab・\sigma _y$$A_b$:ブレース芯材の軸部断面積
$σ_y$:ブレース芯材の降伏応力度
$φ$:ブレースの耐力上昇率
$\phi = P / P_y$$P$:耐力上昇を起こした時の軸力(軸耐力)
$K1$:ブレースの弾性剛性より求めた等価剛性
(2) トリリニアモデル
入力省略時の各パラメータ
| α1 | α2 | K2/K1 | K3/K1 | |
|---|---|---|---|---|
| 値 | 2.00 | 2.50 | 0.06 | 0.02 |
※トリリニアモデルの適用範囲は2.5・Pyまでです。
b) SLY225・SN400B・SN490B
(1) バイリニアモデル
$P$:第1折れ点耐力(= $Py・φ$)
$K_1$:ブレースの弾性剛性より求めた等価剛性
$K_2$: $0.03・K_1$
日鉄エンジニアリング株式会社 アンボンドブレース
アンボンドブレースの履歴特性は標準型バイリニアとします。
詳細につきましては、日鉄エンジニアリングの技術資料をご参照ください。
$P_1$:折れ点耐力(デフォルト = $Ac×F×1.1$)
$Ac$:アンボンドブレースの塑性化部断面積
$K1$:ブレースの1次剛性(等価剛性)
$\phi_A = \frac{E \times Ac}{L}$$φ_A$:パネルゾーン・ブレース弾性部などを考慮した等価剛性倍率
$K2$:ブレースの2次剛性
= K1×剛性低下率 (デフォルト 0.0)
アンボンドブレース(耐震タイプ)一覧
メーカー資料より
○アンボンドブレース(制振タイプ)は下表の通りです。
アンボンドブレース(制振タイプ)一覧
メーカー資料より
日鉄エンジニアリング株式会社 ユニットゴムダンパー
a) 簡易モデル
本粘性ダンパーを、修正HDモデルによりモデル化します。
修正HDモデルは、土の非線形特性を表す履歴モデルとしてよく用いられているHardin-Drnevich(HD)モデルを基に、付加線形バネKaを考慮したものです。
HDモデル 修正HDモデル
(1) 等価剛性 keq(kN/mm)
$$k_{eq} = G_{eq} \times \frac{s}{d}$$$G_{eq}$:等価せん断弾性係数(kN/mm2)
$$G_{eq} = 0.84 \times \gamma^{-0.5}$$ (0.1≦γ≦3.0)
$γ$:歪み
$s$:せん断面積(mm2)
$d$:厚さ(mm)
(2) 等価粘性減衰定数 $h_{eq}$
$$h_{eq} = -0.018 \times \gamma^2 + 0.079 \times \gamma + 0.21$$ (0.1≦γ≦3.0)
(3) 一次剛性 $k_u$(kN/mm)
$$k_u = \beta \times k_{eq}$$(4) (1)~(3)より、降伏荷重特性Qy、初期戻り剛性 $K_0$、付加線形バネ係数 $K_a$を求めます。履歴ループから求まる最大点(Xm,Qm)から最小点(-Xm,-Qm)へ向かう下降曲線と逆の上昇曲線を貸し気で求めます。
$$Q = 2F(X/2-X_m / 2) + Q_m$$ :下降曲線
$$Q = 2F(X/2-X_m / 2) - Q_m$$ :上昇曲線
$$F(X) = X/(1/X_0 + X/Q_y) + K_a \times X$$(5) 以降、その時点での歪に応じて、①~④により履歴ループを逐次算出します。
b) 高精度モデル
(1) 振動モデル
取付バネを考慮し、下図に示すモデルとします。
(2) 静的・動的応力要素の変形( ${}_t \delta _e$)
$${}_t \delta _e = {}_t \delta - \frac{{} _{t-1}Q}{k _g}$$${}_t \delta$:時刻tの要素間変形
${}_{t-1}Q$:時刻t-1の要素力
${k_g}$:取付バネの剛性
(3) 静的応力要素
静的応力要素の履歴特性は、下図に示すように、鋼材と類似する紡鍾型であり、鋼材の履歴の再現に用いられるMenegotto-Pintoモデルを採用します。
(4) 動的応力要素
歪・温度・振動数依存性を再現するため、動的応力要素は、下図に示す粘弾性要素と、非線形粘性要素の並列体で表現します。
粘弾性要素 非線形粘性要素
参考文献:笠井和彦,西澤恵二,大木洋司,田中克往、田中和宏,西本晃治,山崎久雄, 「制振用高硬度ゴムの静的・動的積載実験と時刻歴解析法」, 日本建築学会構造系論文集 Vol.76 No.662
(株)免制震ディバイス RDTダンパー
(1) 軸方向に関する抵抗力
RDTの軸方向に発生する全抵抗力 $P_n$は、RDTの逆効率および正効率を考慮した等価摩擦係数λを介して次式で与えられる。
$$P_n = λ(αQ_v + Q_i + Q_f)$$ ・・・(1)
$P_n$ :RDT の軸方向に発生する全抵抗力(kN)
$λ$ :逆効率および正効率を考慮した等価摩擦係数
$Q_v$ :粘性抵抗力による軸方向力(kN)
$α$ :粘性抵抗力の繰り返しによる低下率
$Q_i$ :回転慣性による軸方向力(kN)
$Q_f$ :静止摩擦による軸方向力(kN)
(2) 粘性抵抗力による軸方向力
粘性抵抗力による軸方向力 $Q_v$は次式で与えられる。
$$Q_v = S・η(V_n,t)・V_s・A$$ ・・・(2)
S :内筒の増幅幅
$η(V_n,t)$:見かけの粘度
$Vs$ :せん断歪速度(1/s)
$t$ :粘性体温度(℃)
$A$ :せん断有効断面積(cm2)
ここに、
$$ V_s = \frac{(S・ \dot{x_n})}{dy} \times 10$$ ・・・(3)
$$η(V_n,t)=\frac{η_t}{(1 + b|V_s|^{\beta})} \times 10^{-10}$$ ・・・(4)
$\dot{x_n}$:軸速度(cm/s)
$d_y$ :せん断隙間(mm)
$η_t$:粘性体温度t℃時の粘度(cSt)
$b,β$ :見かけの粘度を計算する係数
粘性抵抗力の繰り返しによる低下率αは次式で与えられる(初期値:α=1)。
ただし0.7≦α≦1.0
$$\alpha = \frac{1}{(1 + a_1 \frac{E_V}{V_V})^{a2}}$$ ・・・(5)
$E_v$ :粘性抵抗力による累積吸収エネルギー量(j)
$V_v$ :粘性体の充填されている容積(cm3,cc)
$a_1$, $a_2$ :補正係数
ここに、
$$E_v = \frac{1}{2} \Sigma$$$$(α \cdot \Delta Q_v)(\Delta X_n)$$ ・・・(6)
$x_n$ :軸変位(cm)
$i$ :ステップ番号
(3) 回転慣性による軸方向力
回転体の慣性力による軸方向力 $Q_i$は次式で与えられる。
$$Q_i=I \cdot (\frac {2π}{L_d})・\ddot{x_n} × 10^2$$ ・・・(7)
$I$ :回転慣性モーメント(kN・cm・ s2)
$Ld$ :リード長(mm)
$\ddot{x}_n$:軸加速度(cm/s2)
(4) 静止摩擦による軸方向力
静止摩擦による軸方向力Qfは次式で与えられる。
$$Q_f = Q_{si} + Q_{RB}$$ ・・・(8)
$Q_{si}$ :シール材の摩擦による軸方向力(kN)
$Q_{RB}$ :ラジアルベアリングの摩擦による軸方向力(kN)
ここに、
$$Q_{si} = S \cdot (2・2π・r_v・μ_{si})$$ ただし $Q_{si}$は粘性抵抗力 $α_v$と同符号 ・・・(9)
$$Q_{RB} = S_{RB}・\mu_{RB}・W$$ ただし $Q_{RB}$粘性抵抗力 $αQ_v$と同符号 ・・・(10)
$r$:内筒外半径(mm)
$μ_{si}$:内筒外半径(mm):シール材の単位長さ当たりの摩擦力(kN/mm)
$S_{RB}$:ラジアルベアリングの増幅率
$μ_{RB}$:ラジアルベアリングの摩擦係数
$W$ :ラジアルベアリングが支える重量(kN)
(株)免制震ディバイス 粘性制震壁
住友理工 TRCダンパー
振動解析時のモデルは下記の4要素モデルで計算します。静的解析モデルの場合、K2のばねのみ考慮し、非線形を考慮した場合にはK2のBi-linearばねとしてモデル化します。
参考文献:夏堀・千田ほか
「スチレンオレフィン糸粘弾性体を用いた壁型ダンパーの開発、その1~3」
日本建築学会大会学術講演梗概集(2005 年9 月)、21460~21462
JFEシビル株式会社 二重鋼管座屈補剛ブレース
二重鋼管座屈補剛ブレースの履歴特性は標準型バイリニアもしくは辻・山田モデルとします。辻・山田モデルの詳細は「7.8.6辻・山田モデル」に示します。
JFEシビル株式会社 制振間柱
制震間柱の履歴特性はJFE LY トリリニアとします。JFE LY トリリニアの詳細は「7.8.7JFE LYトリリニア」に示します。
JFEシビル株式会社 間柱型粘弾性ダンパー
JFEシビル間柱型粘弾性ダンパーの構成則を以下に示します。第1項は過去に経験した最大せん断ひずみによって剛性が低下するダメージ効果を考慮した非線形ばねを、第2、3 項は塑性項を、第 4 項は Maxwell の粘弾性項を表します。第 2、3 項も過去に経験した最大せん断ひずみによって剛性や減衰が低下するダメージの効果を考慮しています。 $γ_{max}$は過去に経験した最大のせん断ひずみを、Γ はせん断ひずみの変化の絶対値|Δγ|の累積値を表します。
$$\tau(\gamma)= \left(\theta _e + (1 - \theta _e)e^{-\gamma _{max}/\alpha _e} \right) g_e \gamma + \left(\theta _p + (1 - \theta _p)e^{-\gamma _{max}/\alpha _p} \right) g_{p1} \int _\theta^f e^{-(\Gamma-\Gamma^{'})/l_1} \frac{d \gamma^{'}}{d \Gamma^{'}}d \Gamma^{'}$$表2.1 パラメータの同定結果(温度20℃)
ダンパーモデルの概念図
ばらつきは以下のように考慮します。
$$X = x[1-0.026784(y^{2.2481}-1)(y-1.3666)]、Y = y[1-0.026784(y^{2.2481}-1)(y-1.3666)]$$また、温度によるばらつきは、以下のように計算して、上記ばらつきx,yに考慮します。
$$\alpha _T = -9.029 \times 10^{-5}T^2 - 1.668 \times 10^{-2}T + 1.3697$$ $$\beta _T = -2.108 \times 10^{-4}T^2 + 5.958 \times 10^{-3}T + 0.9652$$参考文献:櫻井祐ほか:高減衰ゴムを用いた間柱型粘弾性ダンパー ~その5 性能変動を考慮できる履歴モデル~, 日本建築学会大会学術講演梗概集(東北)2018.9
コンステック CSTダンパー
弾塑性要素、弾性要素、粘性要素から成る三要素モデルとしてモデル化されます。ダンパー部は住友ゴム工業株式会社製粘弾性ダンパー(GR100)でモデル化します
住友ゴム工業 GRASTダンパー
弾塑性要素、弾性要素、粘性要素から成る三要素モデルとしてモデル化されます。
(1)弾塑性要素
静的の加振実験結果から、弾塑性要素の履歴特性を下図のように設定します。
骨格曲線:
$\tau _1 = G_r・\gamma^{\varphi}$(N/mm2)
$τ$ =せん断応力度(τ=F/S)
$γ$ =高減衰ゴムのせん断歪み(γ=δ/t)
$F$ =せん断力
$S$ =高減衰ゴムの断面積
$t$ =高減衰ゴムの厚さ
$δ$ =せん断変形
骨格曲線の勾配も歪み依存であり、 $ks = G_r \cdot \varphi \cdot \gamma^{\varphi-1}$ となります。原点付近ではその勾配が無限大となって定義できないため、極微小の歪み0.001までは線形とします。
除荷後の再降伏曲線は、骨格曲線と比例するように設定します。
再降伏曲線:
$${\tau _1}^{'} = \mu・\tau _1 = \mu・G_r・\gamma^{\varphi}$$過去の最大せん断歪みγmaxを超えない除荷と再載荷は、下図に示すノーマルバイリニア復元力特性を描きます。 骨格曲線から除荷した点は、最大せん断応力度と最大せん断歪み(τmax、γmax) となります。再降伏曲線まで除荷すると、反対側の最大点(-τmax、-γmax)を指向して直線上を再載荷します。除荷勾配ku および第二勾配kp を決めるために、下図に示す除荷カーブの折れ点(τm0、γm0)、つまり、最降伏曲線と第二勾配直線の交差点でせん断歪みγm0は次のように仮定します。
$$\gamma _{m0} = \varepsilon・\gamma _{max}$$ここで、εを次式のように定義します。
$$\varepsilon = \frac{0.94}{1+0.01・\gamma _{max}^{-0.73}}$$交差点(τm0、γm0)は、再降伏曲線上なのでせん断応力度τm0は次のように計算できます。
$$\tau _{m0} = \mu・G_r・\varepsilon^{\varphi} \gamma _{max}^{\varphi} = \mu・\varepsilon^{\varphi} \gamma _{max}$$したがって、除荷カーブの勾配 kuおよび第二勾配 kpは次のように決まります。
$$k_u = \frac{\tau _{max} - \tau _{m0}}{\gamma _{max} - \gamma _{m0}} = \frac{1 - \mu・\varepsilon^{\varphi}}{1 - \varepsilon}・\frac{\tau _{max}}{\gamma _{max}}$$ $$k_p = \frac{\tau _{max} + \tau _{m0}}{\gamma _{max} + \gamma _{m0}} = \frac{1 + \mu・\varepsilon^{\varphi}}{1 + \varepsilon}・\frac{\tau _{max}}{\gamma _{max}}$$正側交差点(τm0、γm0)から負側の最大点(-τmax、-γmax)に向く第二勾配直線:
$$\tau = -\tau _{max} + k_p(\gamma + \gamma _{max}) = \tau _{max}・\left[ \frac{1+\mu・\varepsilon^{\varphi}}{(1+\varepsilon)・\gamma _{max}}・\gamma-1 + \frac{\mu・\varepsilon^{\varphi}}{1+\varepsilon)} \right]$$負側交差点(τ’m0、γ’m0)から正側の最大点(τmax、γmax)に向く第二勾配直線:
$$\tau = \tau _{max} + k_p(\gamma - \gamma _{max}) = \tau _{max}・\left[ \frac{1+\mu・\varepsilon^{\varphi}}{(1+\varepsilon)・\gamma _{max}}・\gamma+1 - \frac{\mu・\varepsilon^{\varphi}}{1+\varepsilon)} \right]$$また、大変形を経験した後の小振幅に対しては下図に示すように、経験最大歪みより得られる菱形ループの対角線(等価剛性)が同じとなる相似形の菱形ループ上を通ります。また、その小振幅の菱形ループから経験最大歪みの菱形ループまで変形が大きくなるときは、等価剛性上をたどります。さらに経験最大歪みを更新するときは、骨格曲線上をたどります。
(2)弾性要素
振動数依存性を考慮した加振実験結果との割線剛性の差を、振動数の増加による付加される剛性として弾性要素で表現します。弾性要素は、実験結果より振動数に依存するこが確認されているため、ダンパー設置前の建物の固有振動数をパラメータとした係数α1 を定めて付加される剛性を表現します。また、弾性要素は経験した最大歪みγ max の依存性を表現し、経験最大歪み以下の小振幅の場合は、その最大歪み時の剛性を保持するように弾性剛性を設定します。
$$\gamma _{max} \leq \gamma _2 \tau _2 = \xi \cdot \gamma$$ $$\gamma _{max} \geq \gamma _2 \tau _2 = \varsigma・\gamma / \gamma^{\psi} _{max}$$γ2は剛性が歪みに依存しない最大歪みの境界値、γ2=0.005 とします。
(3)粘性要素
静的加振以外の加振実験結果より切片応力を求め、その差を加振振動数の増加により付加される応力として粘性要素で表現します。粘性要素の振動数依存性と歪み依存性を歪み速度νで下式のように表現します。
また、粘弾性ダンパーに用いた粘弾性体は、大変形を経験した後、反転時の歪みが同じであっても応力の減少が確認されています。先に算出した弾塑性要素、弾性要素は、経験最大歪みから得られる特性でその応力の減少を表現しています。一方、粘性要素は 歪み速度に用いて表現しているため、経験最大歪みと漸減時振幅の比の関数となる大変形経験後の係数α2 を求める近似式として下式を定義し、その係数をかけて粘性要素の応力の調整をします。
$$\tau _3 = \omega・\nu^{\theta}$$ $$\alpha _ 2 = A・|\gamma _u / \gamma _{max}|^B + C$$(4)初期および未経験領域加振時の応力の増大に対する対応
初期剛性を除去した製品においても初期および未経験領域加振時の応力の増大が確認されています。その応力の増大(付加応力)を速度べき乗型の粘性ダッシュポットとして表現します。
初期および未経験領域加振時 :
$$\tau _4 = \omega _4・\nu^{\theta _4}$$経験領域加振時 :
$$\tau _4 = 0$$なお、この付加応力は歪みを新たに更新するときに生じますが、経験最大歪みγmax を超えてときに突然応力がそのときの歪み速度により増大するのではなく、最大歪みγmax から(1+φ1) γmaxまでの区間は、正弦波の形で付加応力を増大させます。
AFTダンパーシステム
ダンパー、曲げバネ、軸力伝達要素、支持柱から構成されます。ダンパー部は住友ゴム工業株式会社製粘弾性ダンパー(GR100、GR400)でモデル化します。
参考文献:
軸力伝達機構を有する粘弾性ダンパーシステムを用いた工法開発に関する研究
その1.粘弾性ダンパーシステムに対する二軸載荷試験の結果
その2.粘弾性ダンパーシステムを柱に内蔵した実大フレームの静的載荷実験の結果
GBRCの建築技術性能証明評価概要報告書 GBRC 性能証明 第11-20号
Built-in Damper(BiD)フレーム工法-ダンパーを柱に内蔵するアウトフレーム型制振補強工法-
トグル制震ブレース(E&CS*1)
本プログラムでは、トグル制震ブレースの適用に関して、装置の適用範囲の判断は行いません。したがって設計者は、解析から得られた応答値と装置の限界値を別途比較し、装置の適用範囲内であることを確認することが最低限必要です。
ここでトグル制震ブレースには幾何学的非線形性などの特有の条件があり、微小変形解析による本プログラムから得られた応答値をそのまま装置の限界値と比較することができません。装置の適用範囲の確認においては、解析から得られた応答値を、幾何学的非線形性の考慮を含む特殊な割り増し計算を行った後に装置の限界値と比較する必要があります。
この特殊な割り増し計算を含めた装置の適用範囲の確認方法については、(株)E&CS*1が提供する「トグル制震構法 技術情報シート」(http://www.kk-ecs.co.jp/engineering_sheets/)を参照してください*2。また同技術情報シートには装置の適用範囲の他にも技術的な情報が示されています。
*1 (株)E&CSは、「トグル」および「トグル制震ブレース」について、知的財産権を所有する飛島建設(株)より許諾を受けて使用しています。
*2 「トグル制震構法 技術情報シート」の適用範囲を超える設計を行った場合、(株)E&CSから装置の提供ができない場合があります。
【腕軸剛性】
腕軸剛性K1 :以下の計算により算出する。
1/K1=1/(A・Es/Lu)+1/Kcf+1/Kcm+1/Kg
$A$ :腕鋼管断面積
$Es$ :鋼材のヤング係数
$Lu$ :腕鋼管の長さ $Lu=L1$-(腕両端クレビス長さの和)
クレビス長さ :腕鋼管端とクレビスピン穴芯間長さ
$L1$ :剛性計算用腕長さ $L1=Lm-Lr$
$Lm$ :トグルモデル腕長さ(構造芯節点とトグル中央交点ピン穴芯間長さ)
$e0$ :柱面または梁面とピン穴芯間の最小長さで以下による
| トグル種類 | e0値 |
|---|---|
| 850KNダンパー用 | 165mm |
| 500KNダンパー用 | 135mm |
| 300KNダンパー用 | 100mm |
$Lr$ :e0寸法で決まるピン穴芯と構造芯節点間の最小長さ
$dc$ :柱面と構造芯間長さで以下とする $dc$=(左右の柱成寸法の平均)/2
$dg$ :梁面と構造芯間長さで以下とする $dg$=(上下の梁成寸法の平均)/2
$Kcf$ :建物架構側クレビスの軸剛性
$Kcm$:トグル中央節点側クレビスの軸剛性
$Kg$ :ガセットプレートの軸剛性
【腕構面内曲げ剛性】
腕構面内曲げ剛性I1 : 以下の計算により算出する
$I1$ = $(Lm/L1)_3・I$
$I$ : 腕鋼管の断面二次モーメント
【腕構面内せん断剛性】
腕構面内せん断剛性As1 : 以下の計算により算出する
$As1$ = $(Lm/L1)・As$
【腕軸非線形特性】
腕軸の非線形特性は以下のように設定します。履歴則は逆行型とします。
【ダンパー非線形特性】
ダンパーの非線形特性はリリーフ荷重によるバイリニアとして設定します。
履歴特性
履歴特性
逆行型
常にスケルトンカーブ上を進みます。
標準型
除荷履歴はMasing則(相似則)により決定されます。除荷開始時の剛性は初期剛性となり、除荷後の第2剛性、第3剛性は骨格曲線の剛性低下率と同様になります。
原点指向型
初期履歴ではスケルトンカーブ上を進み、その直線上から戻って反対方向に進むときは原点を通る直線上を進みます。
最大点指向型
(1) $|max|<δ_{y1}$の場合は、原点を通る勾配 $K_1$の直線上を動きます。
(2) $δ$がはじめて $±δ_{y1}$または $±δ_{y2}$を超えた時点、あるいはこれまでの最大変形 $δ_{max}$を超えた時点で、スケルトンカーブ上の第2勾配 $K_2$または第3勾配 $K_3$の直線上を進みます。この直線上を戻って反対方向に進む場合は、戻り点から(この $δ$が新しく $δ_{max}$となる)反対側の、今までの最大変形点を目指します。
武田型
(1) $|max|<δ_{y1}$の場合は、原点を通る勾配 $K_1$の直線上を動きます。
(2)
ⅰ)
$δ$が
$δ_{y1}$をこえた場合、スケルトンカーブ上の第2勾配
$K_2$の直線上を進みます。
ⅱ)この直線から戻って反対方向に進む場合は、戻り点(この $δ$が新しい $δ_{max}$となる)から反対側の第1折点を目指します。
$${K_d}^+ = K_0 \times \left| \frac{{\delta^+}_{max}}{\delta _{y2}} \right|^{-\nu}$$ⅲ)反対側の最大変形が弾性域の場合は、この剛性域の範囲は反対側の第1折点までとします。
ⅳ)反対側の最大変形が $δ_{y1}$をこえている場合は、この剛性域の範囲は復元力が0となる点までとします。そして、この0点をこえた場合は、反対側の最大変形点を目指します。更に、この最大変形点を目指す直線から戻る場合以降の規則は、図を参照して下さい。
ⅴ)最大変形点をこえた場合は、スケルトンカーブ上の第2勾配 $K_2$の直線上を進みます。
(3)
ⅰ) $δ$が $δ_{y2}$をこえた場合、スケルトンカーブ上の第3勾配 $K_3$の直線上を進みます。
ⅱ)この直線上を戻って反対方向に進む場合は、戻り点(この $δ$が新しい $δ_{max}$となる)から、下式で求まる勾配 $K_d$の直線上を進みます。
ⅲ) 反対側の最大変形が $δ_{y1}$をこえていない場合は、勾配 $K_d$の範囲は反対側の $Q_c$までとします。更にこの $Q_c$をこえた場合は、第2折点を目指します。
ⅳ) 反対側の最大変形が $δ_{y1}$をこえている場合は、勾配 $K_d$の範囲は復元力0の点までとします。更にこの0の点をこえた場合は、最大変形点を目指します。ただし、反対側の最大変形が $δ_{y2}$をこえていない場合は第2折点を目指します。また、この場合は $δ_{max}=δ_{y2}$となります。
ⅴ) ⅲ)において、第2折点を目指す直線上から戻る(この $δ$が新しい $δ_{max}$となる)場合は、勾配 $K_0$の直線上を進みます。更に復元力0の点をこえると、最大変形点を目指します。この最大変形点を目指す直線上から戻る場合は、上式で求まる勾配 $K_d$上を進み、復元力0をこえると、反対側の最大変形点を目指します。
ⅵ) ⅳ)において、最大変形点を目指す直線上から戻る(この $δ$が内部ループの最大変形 $_iδ_{max}$となる)場合は、勾配 $K_d$上を進み、復元力0の点をこえると、最大変形点を目指します。この最大変形点を目指す直線上から戻る(内部ループの反対側の最大変形 $_iδ_{max}$とする)場合も、勾配 $K_d$上を進み、復元力0の点をこえると内部ループの最大変形点を目指します。
ⅶ) ⅳ)において、内部ループの最大変形点をこえてスケルトンカーブ上の最大変形点に向かって動いている途中で、反対方向に進む場合は勾配 $K_d$上を進み、復元力0の点をこえると、反対側のスケルトンカーブ上の最大変形点を目指します。
【参考文献】
Takeda, Sozen and Nielsen : Reinforced Concrete Response to Simulated
Earthquakes, Journal, Structural Division, ASCE, Vol.96,No.ST12,1970
ⅶ)の説明図
A→B→…→Kと進みます。
辻・山田モデル
辻・山田モデルのスケルトンは、バイリニアです。スケルトン情報以外に、辻・山田モデル用β値の設定を行う必要があります。辻・山田モデルは、以下に示す法則に従って動きます。
(1) $δ_n ≤ δ ≤ δ_p$の場合、原点を通る勾配 $K_1$の直線上を動きます。
(2) i) $δ$が $δ_n$および $δ_p$を越えた場合、勾配 $K_2$の直線上を進みます。
ii) この直線上の点( $δ_1$, $Q_1$)から戻って反対方向に進む場合は、勾配 $K_1$で以下の点( $δ_2$, $Q_2$)を目指します。( $δ_2$, $Q_2$)は点 $A_1$を通る勾配 $K_2$の直線との交点です。
ここに $ΔQ_1$ :等方硬化開始点と除荷点との耐力差
正側で初降伏の場合: $ΔQ_1=Q_1-Q_p$
負側で初降伏の場合: $ΔQ_1=Q_1-Q_n$
$β$ :辻・山田モデル用
$β$値
$(0.0≦β≦1.0)$
$d$ :変形
$d_p$ ,
$d_n$:降伏変形
iii) ( $δ_2$, $Q_2$)を目指している途中で反対方向に進む場合は、勾配 $K_1$で( $δ_1$, $Q_1$)を目指し、( $δ_1$, $Q_1$)に到達した場合、勾配 $K_2$の_直線上を進みます。
iv) ( $δ_2$, $Q_2$)に到達した場合、勾配 $K_2$の直線上を進みます。
(3)
i) 勾配 $K_2$を進行中、( $δ_3$, $Q_3$)より反対方向に進む場合は、勾配 $K_1$で以下の点( $δ_4$, $Q_4$)を目指します。( $δ_4$, $Q_4$)は点 $A_2$通る勾配 $K_2$の直線との交点です。
ii)( $δ_4$, $Q_4$)に達した後は、勾配 $K_2$で進みます。
【β値】
辻・山田モデル用 $β$値とは、移動硬化と等方硬化の割合を決定するパラメータです。
$\Delta \bar{\sigma} = \beta \left| \Delta \sigma \right|$ $\Delta \bar{ \alpha } = (1 - \beta) \left|\Delta \sigma \right|$ここに、
$\Delta \sigma$:剛性変更点からの増分応力
$\Delta \bar{\sigma}$:等方硬化が負担した増分応力(降伏幅の膨張)
$\Delta \bar{\alpha}$:移動硬化が負担した増分応力(降伏幅中心の移動)
$β=1.0$の場合、剛性変更点から塑性化した応力分だけ降伏幅が膨張します。つまり、塑性化した符号の反対側の剛性変更点も同様の値となります。逆に、 $β=0.0$の場合、降伏幅の変更は起こらず、中心のみが移動するループを描く(耐力が正負同じ場合は、「標準型」と同様のループ)ようになります。
JFE LYトリリニア
履歴則を以下に示します。
(1) 基本ルール
1) $|δmax|<δ_y$の場合、原点を通る勾配 $K_1$の直線上を動きます。
2) $δ$が初めて $±δ_y$を越えた場合は、第2勾配 $K_2$(= $β・K_1$)の直線上を進みます。
3) 2)の直線上を戻って反対側に進む場合は、戻り点から勾配 $K_1$にて進み、反対側の第2勾配を規定する直線( $-Q_d$を通る勾配 $P_3・K_1$の直線)の交点まで進みます。折れ点以降は、第2勾配 $K_2$(= $β・K_1$)の直線上を進みます。
4) 3)の直線上を戻って、反対側に進む場合は、3)の規則を繰り返します。
注)現在プログラム内部において、 $P_2=0$としている。
(2) 履歴ループが第3勾配の直線と交差した場合は、以下の基本ルールに従うものとします。
1) 第2勾配で進み、第3勾配の直線(図の一点波線内)を越えた場合、その直線上第3勾配 $K_3$(= $P_2・K_1$)の直線上を進みます。
2) 1)の直線上を戻って反対側に進む場合は、戻り点から勾配 $K_1$にて進み、反対側の第2勾配を規定する直線( $-Q_d$を通る勾配 $P_2・K_1$の直線)の交点まで進みます。折れ点以降は、第2勾配 $K_2$(= $β・K_1$)の直線上を進みます。
3) 2)の直線上を戻って反対側に進む場合は、2)の規則を繰り返します。
4) ただし、下図のように $K_1$で進む直線が、第2勾配を規定する直線と交差する前に第3勾配と交差する場合は、直接第3勾配で進みます。(次項図④の直線を参照)
注)現在プログラム内部において、 $P_2=0$としている。
その他の解析機能
その他の解析機能
位相差入力解析
下記の計算式により、位相遅れ時間を計算します。
$V_s$ :せん断波速度 $(m/s)$
$L$ :矩形基礎長さ $(m)$
$θ$ :入射角 $(°)$
$t$ :位相遅れ時間
$L$ = $L_x$ または $L_y$
位相遅れ方向 X方向 → $L_x$
位相遅れ方向 Y方向 → $L_y$
$t = ( L × sinθ) / V_s$
上記位相遅れによってねじれ加速度時刻歴波形を作成し、並進方向加速度時刻歴波形と同時加振することにより位相差を考慮します。
鉄骨梁端部の累積損傷度計算
指定により、鉄骨梁端部の累積損傷度を計算できます。 累積損傷度の計算は以下の方法から選択できます。
- レインフロー法
- 累積塑性変形倍率(最大振幅)
- 累積塑性変形倍率(振幅頻度分布一様)
レインフロー法
梁端曲げ塑性率の振幅を用いて、レインフロー法によるサイクルカウントを行います。
塑性率の振幅は振れ幅としてカウントされるため、片振幅としてカウントされた振幅を $1/2$ した値を塑性率 $μ$ として、以下の計算を行います。
$N_{fi}$ : 振幅
$i$ による破断寿命
$N_{ei}$ : 振幅
$i$ による繰り返し回数
$D_{i}$ : 振幅
$i$ による累積損傷度
$N_{fi} = (\frac{\mu}{C})^{-\frac{1}{\beta}}$
$D_{i} = N_{ei} / N_{fi}$
$D = \sum(D_i)$
累積塑性変形倍率
梁端曲げ復元力特性の履歴から、累積塑性変形倍率を算出します。
累積塑性変形は、 $M-θ$ 履歴においてX軸を横切った変形分を累積することにより求めます。
算出された累積塑性変形倍率を用い、以下のように累積損傷度を計算します。
$D = \frac{\eta}{4(\mu_{max}-1)}(\frac{\mu_{max}}{C})^{\frac{1}{\beta}}$ (最大振幅の場合)
$D = \frac{\eta \mu_{max}}{2(1+\frac{1}{\beta})(\mu_{max}-1)^2}(\frac{\mu_{max}}{C})^{\frac{1}{\beta}}$ (振幅頻度分布一様の場合)
08. 免震層の設計
08. 免震層の設計のサブセクション
免震層偏心率の計算
免震層偏心率の計算
計算方法
剛心計算用の免震部材の剛性は、「免震層設計条件」で設定された「免震層想定変形」に基づいた等価剛性として計算します。剛性の計算方法は「免震層偏心率計算・固有値解析モデルの剛性」と同様です。
出力例
免震層上下大梁の検定
免震層上下大梁の検定
設計用応力
大梁の設計用応力は1次設計時の応力を用います。
免震部材のせん断力による付加曲げモーメント
「応力計算条件」-「免震装置のモデル化」において、「せん断力によって発生するモーメントを考慮する」としている場合には1次設計用のモーメントに免震部材のせん断力による付加曲げモーメントが含まれています。「せん断力によって発生するモーメントを考慮しない」としている場合には、免震上下大梁の断面検定時に応力として加算します(免震設計計算書)。このとき、採用する $Q-h$モーメントは、「 $P-δ$、 $Q-h$付加曲げ計算用層間変位」で入力された変位が発生した際に各支承材に発生するせん断力を用いて計算されます。
免震部材のP-δ効果による付加応力
「免震層設計条件」-「免震層上下大梁設計時の $P-δ$効果による付加曲げモーメント」の「 $P-δ$、 $Q-h$付加曲げ計算用層間変位」で入力した層間変位 $δ$から付加曲げモーメントを計算します。 $P-δ$効果による付加曲げモーメントは支承材タイプにより計算方法が異なります。 $P-δ$効果による付加曲げモーメントを計算する際に、上下動係数を考慮するか否かは計算条件により設定可能です。
・付加曲げモーメントは免震部材の軸力が引張のときには $0$とします。
・付加曲げモーメントは、左端・右端それぞれにおいて水平荷重時のモーメントと同じ符号としてモーメントを割り増す方向に作用させます。
・端部以外のモーメントは左端・右端から線形補間により計算します。
・支承材がない位置の付加曲げモーメントは $0$とします。
・付加せん断力は ( $M_{pd}+M_pd/L$ により計算します。
( $_LM _{pd}$:左端付加曲げモーメント、 $_RM _{pd}$:右端付加曲げモーメント、 $L$:材長)
・大梁を分割して入力し、支承材が抜ける箇所がある場合には下記のように付加応力が計算されるため注意が必要です。その場合、一本部材指定を行うことで付加応力を適切に評価することが可能です。
大梁が分割されて支承材が配置されない箇所がある場合の仮定
$P-δ$効果による付加応力は支承材のタイプにより以下のように計算されます。
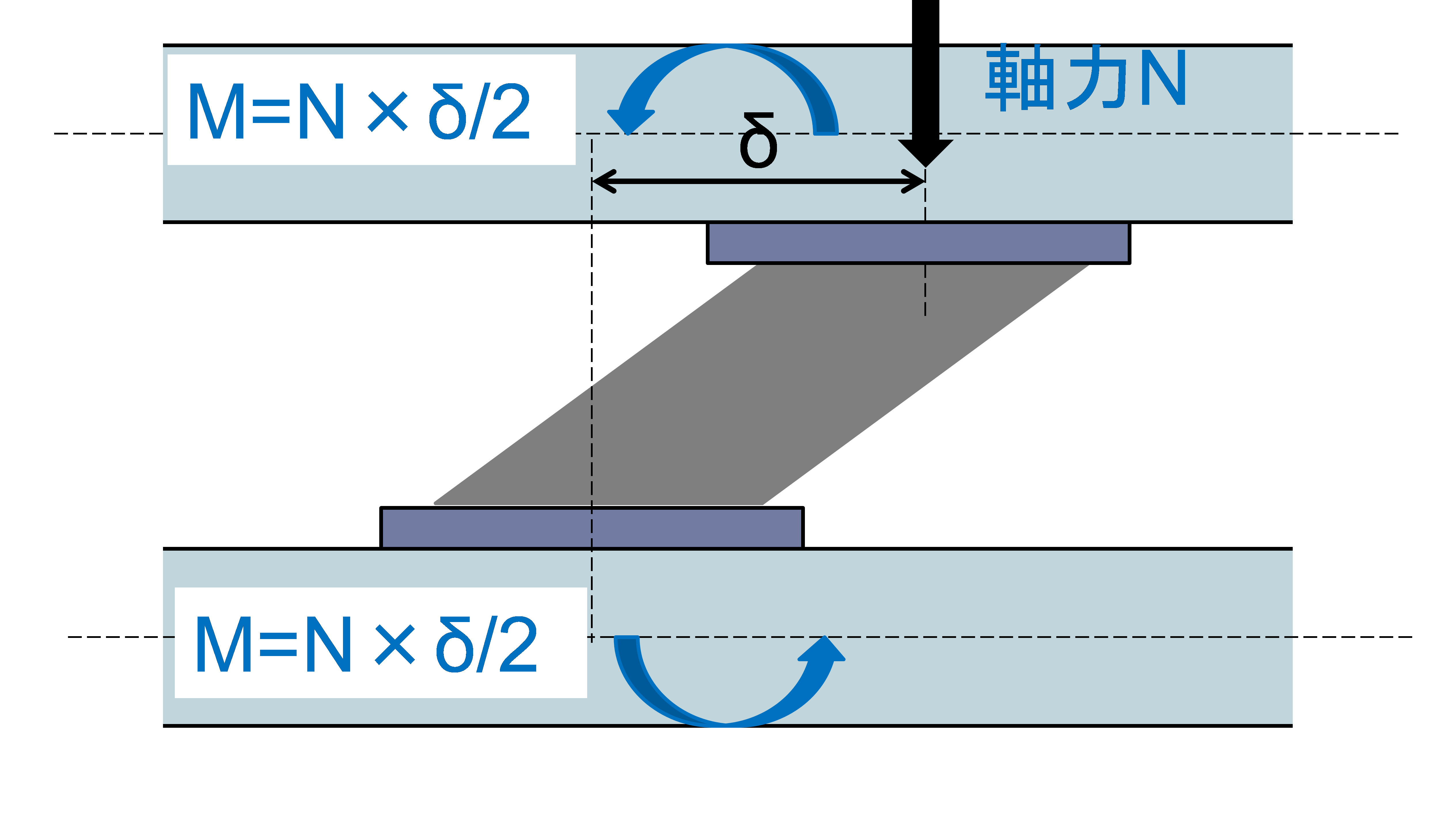
積層ゴム支承(すべり、転がり支承以外)
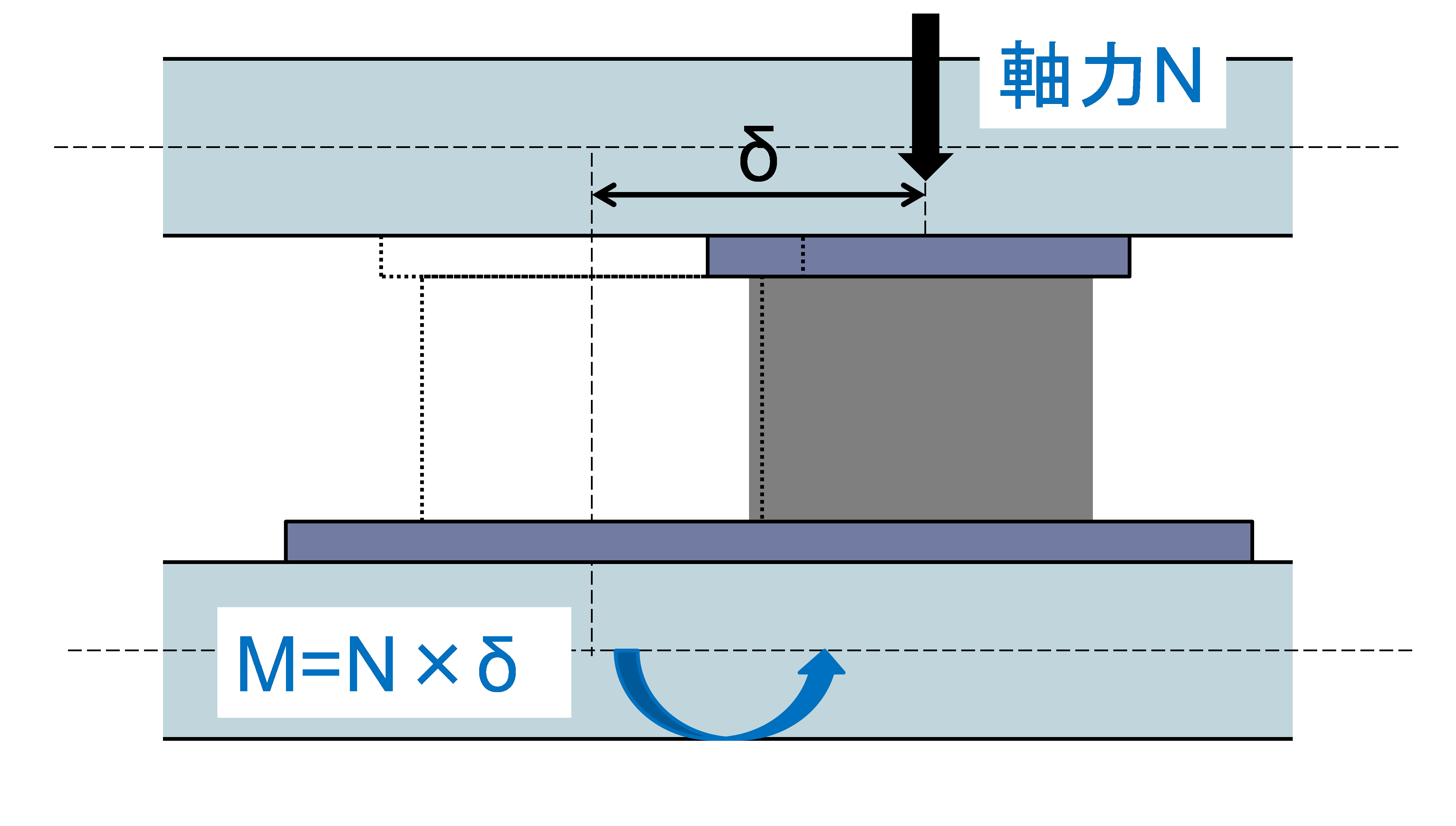
すべり支承(すべり面が下側の場合)
また、大梁ごとに「 $P-δ$付加曲げを無視する」の指定を行うことが可能です。これは配置形状から、 $P-δ$による付加曲げを負担すべきでないと判断される大梁がある場合のための機能になります。たとえば、大梁として配置されている片持ち梁などが該当します。この指定をした大梁が $P-δ$付加曲げ計算対象となる節点の周辺に存在する場合、指定された大梁以外の大梁で付加曲げを分配して計算されます。
固有値解析
固有値解析
計算方法
「免震層設計条件」で設定された「免震層想定変形」から計算した免震部材の剛性を考慮した固有値解析を行います。また、免震部材を十分に硬くした固有値解析も行います。
出力例
質点系固有値
立体固有値
免震部材の面圧検定
計算方法
各免震部材の許容面圧に応じて、振動解析結果の面圧が許容値を超えていないかどうかをチェックします。各部材の面圧・歪みは以下とします。指定による静的解析結果を採用することも可能です。
a) 立体振動解析結果
面圧 :
・(静的解析結果を用いる場合)1次設計時軸力による免震部材の面圧
・(動的解析結果を用いる場合)振動解析結果による免震部材の面圧±上下震度による面圧
※水平上下同時入力を行った場合には、上下震度を設定しておくと重複して評価されることに注意が必要です。歪み :
・クライテリア変形時
・(動的解析結果を用いる場合)最大応答変形
b) 質点系振動解析結果
面圧 :
・1次設計時軸力による免震部材の面圧±上下震度による面圧
※OTM低減係数を設定した場合、水平荷重時軸力にOTM低減係数を乗じた値を水平荷重軸力として採用します。歪み :
・クライテリア変形時
・(動的解析結果を用いる場合)免震層最大応答変形から計算される歪み
出力例
・検定比図 (発生面圧)/(各ひずみによる許容面圧)
・部材種類ごとの面圧詳細図
09. 数量積算
09. 数量積算のサブセクション
各部位共通事項
各部位共通事項
鉄筋コンクリート造
(1)鉄筋
鉄筋のフック、余長、重ね継手長さ及び溶接継手長さについては考慮していません。
鉄骨造
(1)鉄骨
鉄骨重量は次のように計算します。
・鉄骨鋼材の場合
$ W=L \times A \times 7.85$ここで、 $W$:鉄骨重量、 $L$:鋼材長さ、 $A$:鋼材断面積、 $7.85t/m^3$:鉄骨単位重量(固定値)
鉄骨鉄筋コンクリート造
(1)コンクリ―ト
コンクリート体積は鉄骨体積を差し引かずに計算します。
基礎梁・基礎フーチング
基礎梁・基礎フーチング
(1)コンクリート
・ハンチなしの場合: $B×D×L$
・ハンチ付きの場合: $B×D×L+\frac{[(B+B_i)×(D+D_i)]×L_i}{A}+\frac{[(B+B_j)×(D+D_j)]×L_j}{A}$
※寸法のとり方は「大梁」の図を参照のこと。
(2)型枠
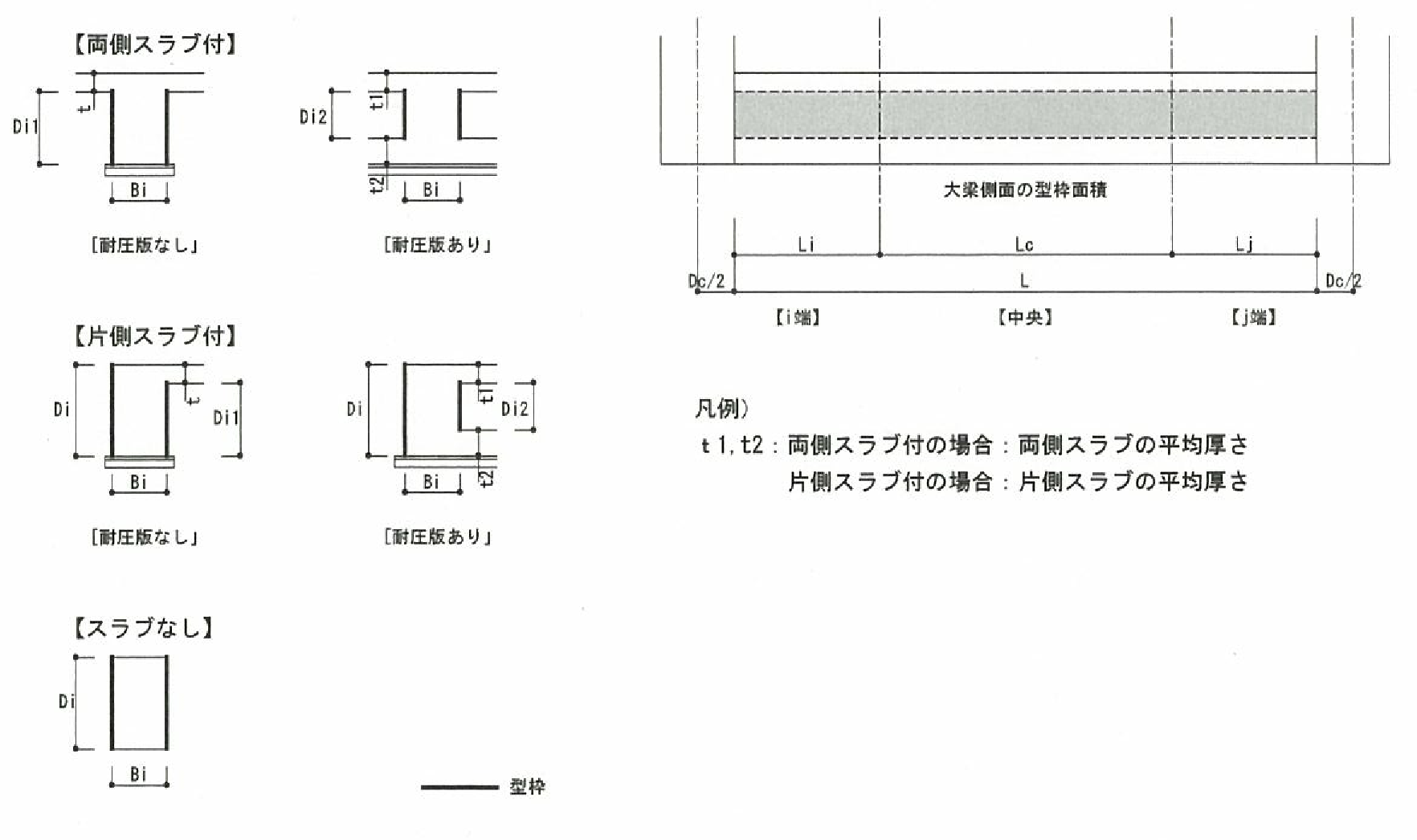
型枠面積: $D×L+\frac{(D_i-D×L_i)}{2}+\frac{(D_i-D×L_i)}{2}+B×L+(B_i-B)×L_i+(B_j-B)×L_j$
※ $D$, $D_i$, $D_j$については、上図のようにスラブ(2重スラブを指定した場合の耐圧版を含む)の有無により適宜スラブ厚さを控除します。また、片持ちスラブが取り付く場合も一般スラブが取り付く場合と同様に取り扱います。
(3)鉄筋
主筋、スターラップは大梁を参照。
(4)鉄筋継手
基礎梁ごとに0.5個所の継手があるものとみなし、基礎梁の長さ $L$が5.0m以上の場合は5.0mごとに0.5個所の継手を加えて計算します。 圧接の場合は、継手個所数を集計します。
(5)基礎フーチング
①コンクリート
コンクリート体積: $B×D×h$
②型枠
型枠面積: $2×(B+D)×h+B×D$
③鉄筋
下端筋を $D13@200$と仮定して算定します。鉄筋長さは $B(D)$とし、端部の定着は考慮しません。また、はかま筋(上端筋) $D13@400$で計算します。
柱
柱
(1)寸法のとり方
柱長さは床上~床上を柱長さとして計算します。
(2)コンクリート
コンクリート体積= $D_x \times D_y \times H$
$H$:柱長さ
(3)型枠
型枠面積= $2×(D_x+D_y)×H$
(4)鉄筋
X,Y方向で鉄筋径が異なる場合には、隅の重なり合う部分は差し引かずに計算します。
- 主筋
すべての柱はHで計算します。
- フープ
フープ筋の長さ = $n_x×D_x+n_y×D_y$
$n_x$:X方向一組のフープ本数
$n_y$:Y方向一組のフープ本数
柱フープ本数 = 柱内法部分フープ本数
柱内法部分フープ本数= $H/cP$
(5)鉄筋継手
柱頭・柱脚通しの主筋は階ごとに1個所継手があるものとみなし、階高が7.0m以上の場合は7.0m毎にさらに1個所の継手を加えます。
※柱頭・柱脚通しの主筋の本数=min(柱頭の本数、柱脚の本数)とします。
(6)鉄骨
各節毎、または各階毎に種類別の長さと重量を算出します。柱頭と柱脚で鋼材サイズが変わる場合は、継手位置を考慮します。
大梁
大梁
(1)寸法のとり方
端部にハンチがある場合にはこれを考慮して計算します。
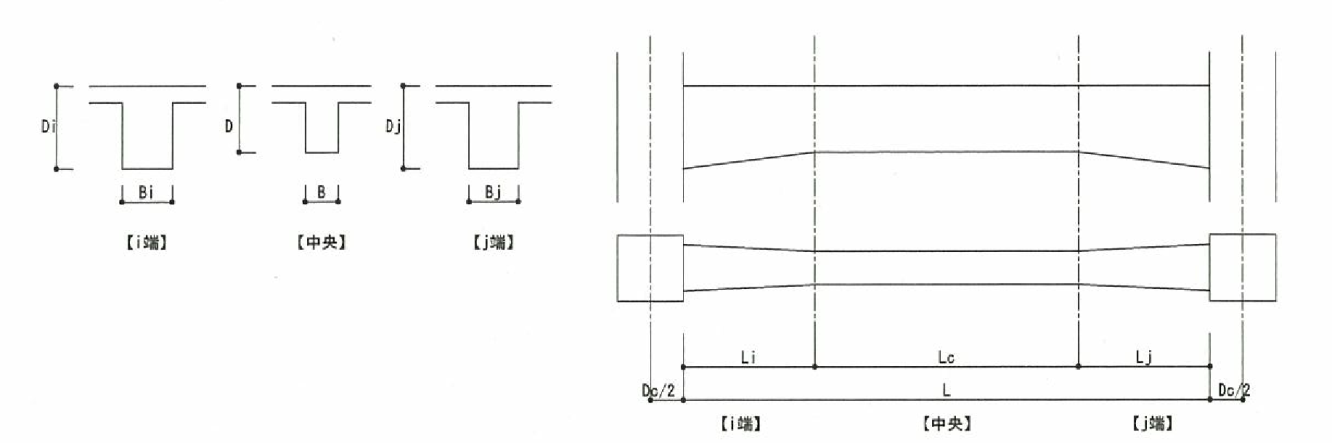
(2)コンクリート
・ハンチなしの場合: $B×D×L$
・ハンチ付きの場合:上記にハンチ部分の体積を加算します。
(3)型枠
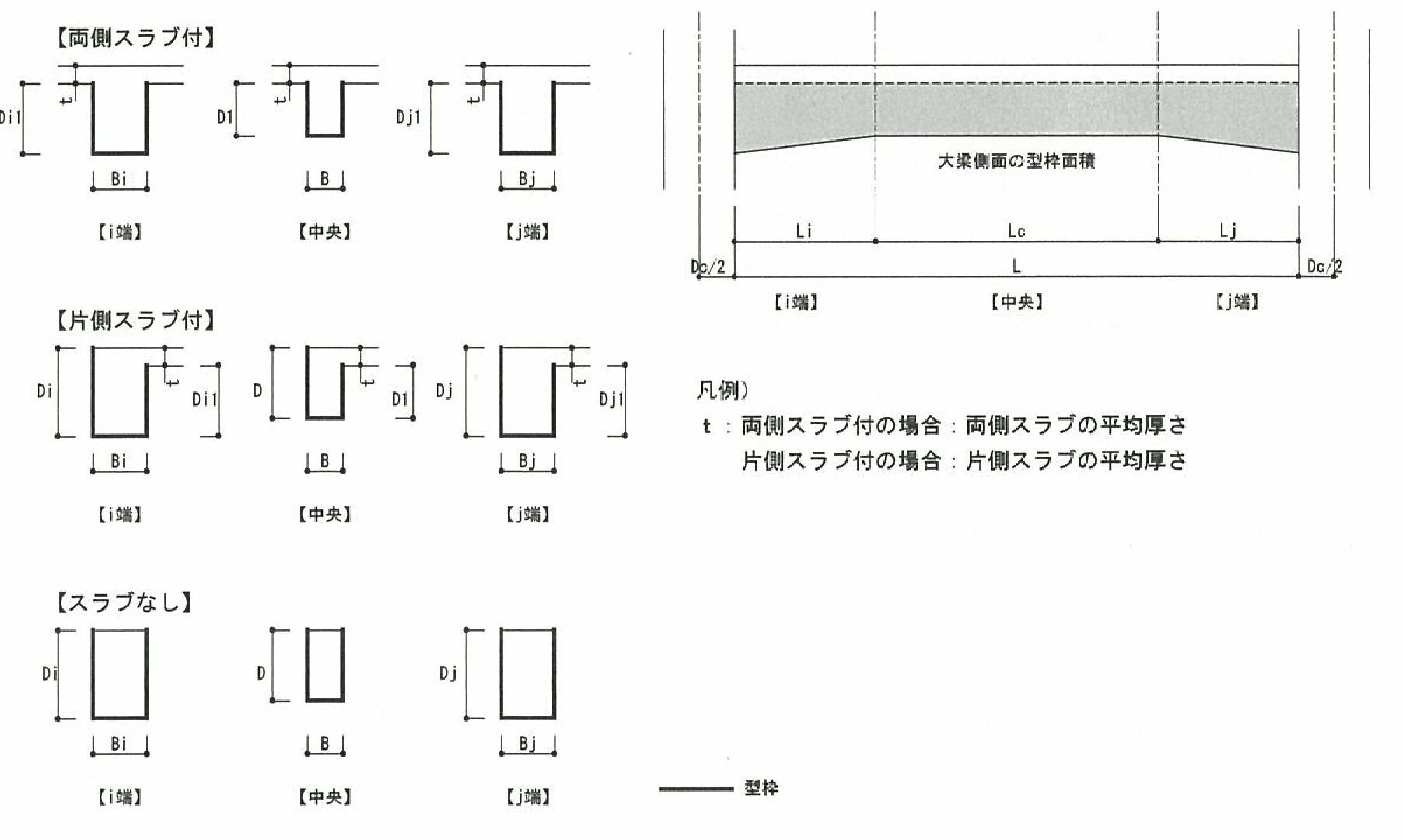
型枠面積: $(D×L+\frac{D_i-D}{2}×L_i+\frac{D_j-D}{2}×L_j)×2+B×L+\frac{B_i-B}{2}×L_i+\frac{B_i-B}{2}×L_j$
※上記の式は両側スラブ厚が等しい場合のものです。
※ $D,D_i,D_j$については、上図のようにスラブ(2重スラブを指定した場合の耐圧版を含む)の有無により適宜スラブ厚さを控除します。また、片持ちスラブが取り付く場合も一般スラブが取り付く場合と同様に取り扱います。
※ハンチ部分の型枠は傾斜を無視し、大梁底面または側面に対する投影面積で計算します。
(4)鉄筋
- 主筋
主筋の長さは大梁の断面数に応じて次のように算定します。
1断面(全断面) :大梁の全長について算定
2断面(両端・中央) :端部と中央部に分けて算定
3断面(外端・中央・内端):外端・内端及び中央部に分けて算定
計算式は下図によります。
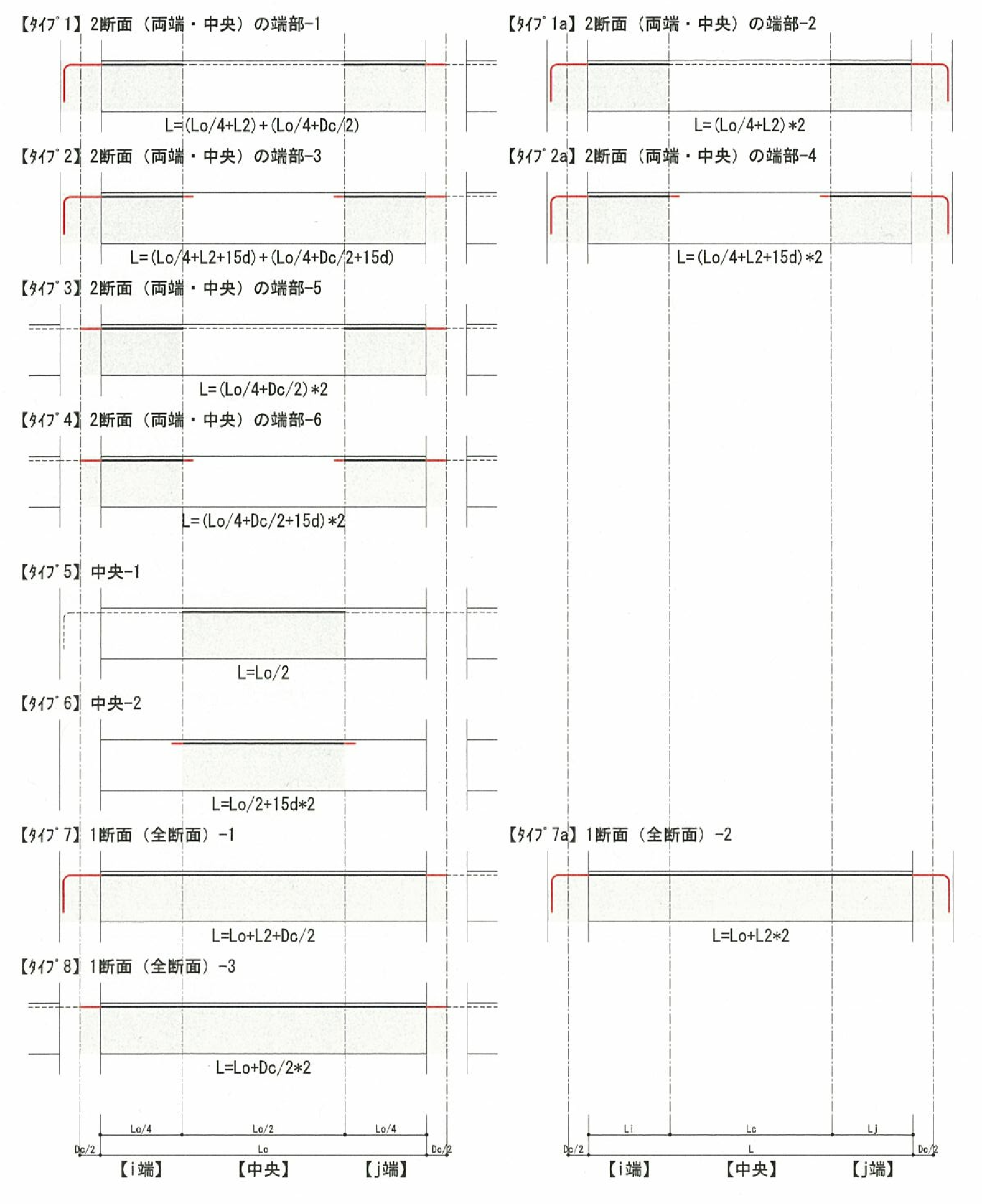
- スターラップ
スターラップ長さ= $2×B+n×D$
$n$:一組のスターラップ本数
(5)腹筋
段数は入力値、腹筋長さ= $L$として計算します。
(6)幅止筋
幅止筋長さ= $B$
(7)鉄筋継手
梁毎に0.5個所の継手があるものとみなし、梁の長さ $L$が5.0m以上の場合は5.0m毎に0.5個所の継手を加えて計算します。
小梁
小梁
(1)寸法のとり方
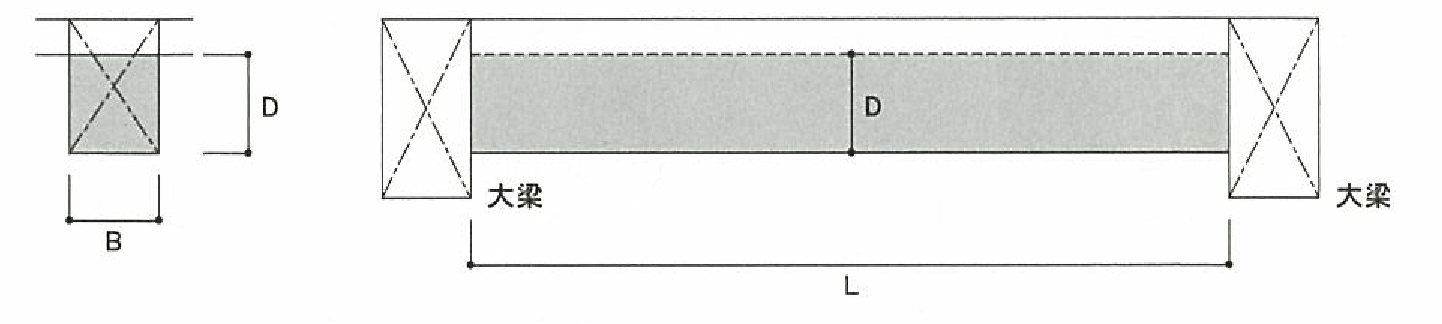
注)2次小梁の長さは大梁(小梁)芯間の距離とします。
(2)コンクリート
コンクリート体積= $B×D×L$(床荷重表で入力した値)
*デッキスラブの場合デッキ高さ分のコンクリートは拾いません。
(3)型枠
型枠面積= $(B+2×D)×L$
(4)鉄筋
- 主筋
主筋重量 :小梁コンクリート体積×0.8(%)
- スターラップ
スターラップ重量:小梁コンクリート体積×0.1(%)
床
床
(1)寸法のとり方
床面積は大梁内法で囲まれた範囲のうちで、小梁で区切られた部分ごとに計算し、床が配置されていない部分については計算しません(下図参照)。床と小梁の重なり部分は床に含めて計算します。
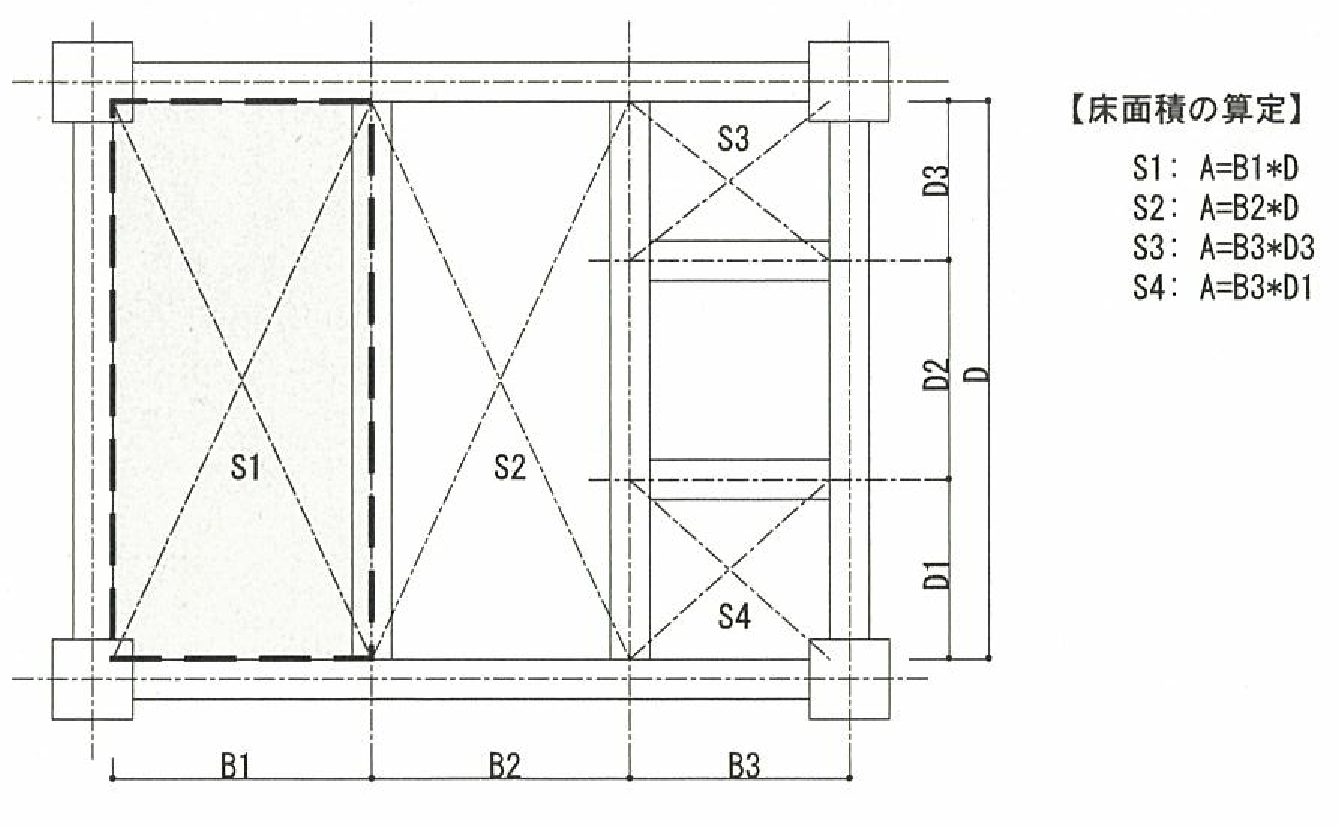
(2)コンクリート
コンクリート体積=面積×床厚(床荷重で入力した値)
*デッキスラブの場合、デッキ高さ部のコンクリートは拾いません。
(3)型枠
型枠面積=面積
(4)鉄筋
鉄筋重量:床コンクリート体積×1.0(%)
片持ち床、出隅、入隅
片持ち床、出隅、入隅
(1)寸法のとり方
片持ち床・出隅は、長方形として計算します。
入隅は長方形×2として計算し、面積は、大梁、片持ち梁、小梁、リブ間の内法とし、柱による欠除は考慮しません。
(2)コンクリート
コンクリート体積=面積×床厚
(3)型枠
型枠面積=面積
片持ち梁については、先端リブ、片持ち床等が何も取り付いていない側面の型枠も計上しています。
(4)鉄筋
鉄筋重量:床コンクリート体積×1.0(%)
壁
壁
耐震壁及びフレーム内雑壁
(1)寸法のとり方
壁の幅は柱内法距離、壁高さは梁内法高さとし、柱及び大梁による欠除を考慮します。
また開口部分の面積を考慮します。
(2)コンクリート
コンクリート体積=面積×壁厚
(3)壁枠
壁枠面積=面積×2
(4)鉄筋
横筋 : $(L+2S)・W$
縦筋 : $(H+2S)・h$
開口部補強筋:考慮していません。
$S$ :定着長さ $(35d)$
ブレース
ブレース
各階ごと、部材符号毎に種類別の長さと重量を算出します。
(1)寸法のとり方
ブレースの長さは節点間距離として計算します。
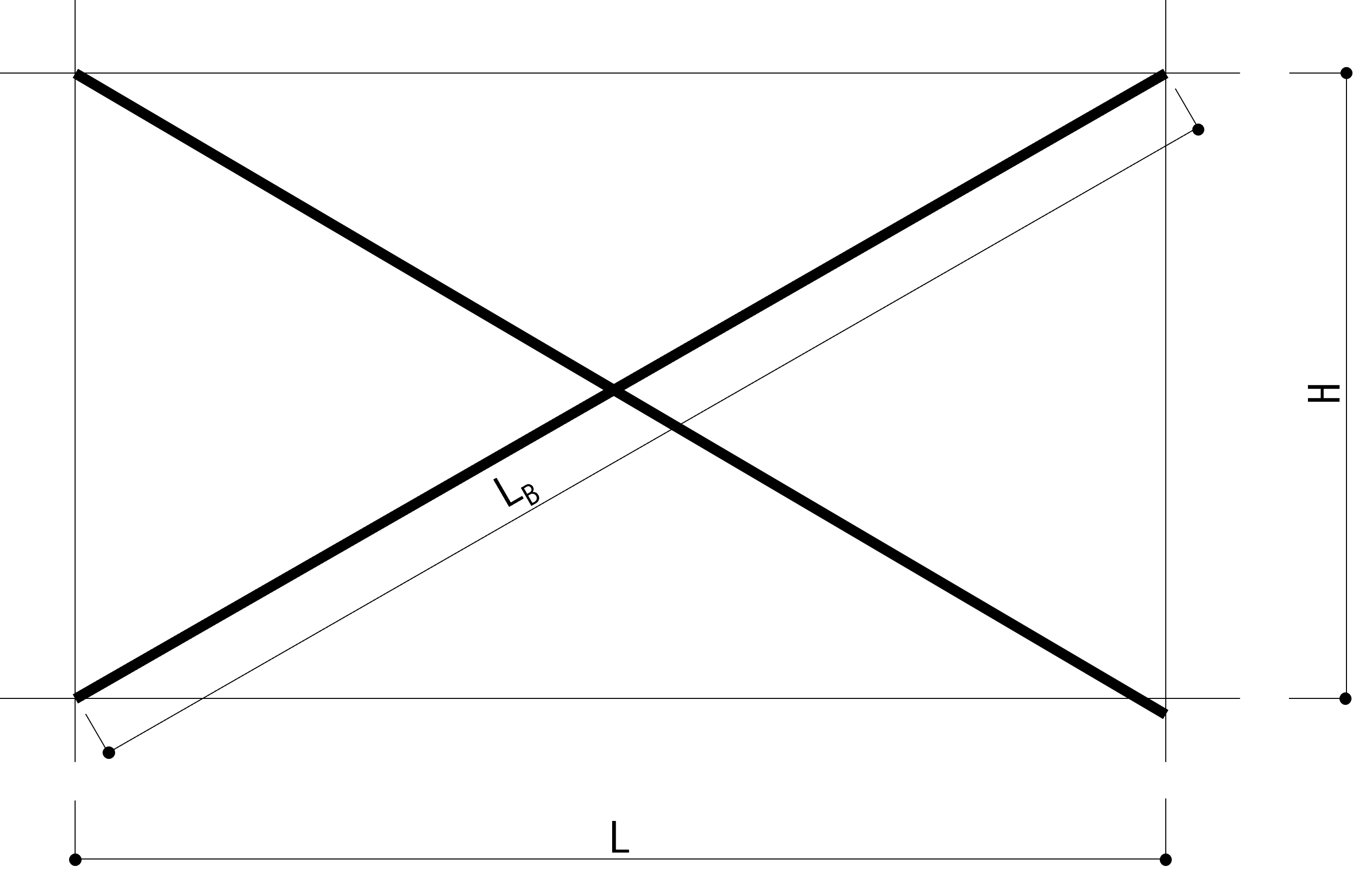
$L_B$ :ブレース長
$H$ :階高
$L$ :スパン長
(2)その他
接合部のプレート、ボルト等は考慮しません。
10.その他計算機能
10.その他計算機能のサブセクション
ドキュメント出力
ドキュメント出力
鉄骨ロングスパン大梁の検討
鉄骨ロングスパン大梁の検討を行います。
弾性、弾塑性が選択できます。
柱MN相関の検討
柱のMN相関の検討を行います。 検討は1軸曲げをベースにした検討となります。 そのため、2軸曲げを考慮している一覧表と整合しない場合があります。
柱2軸曲げの検討
柱の2軸曲げの検討を行います。
45°加力時の柱の評価を行う場合などの機能です。
2つの検討方法があります。
- a) X,Y方向加力を組み合わせ、45°加力時の応力を作る
- b) 解析された加力方向による応力をそのまま採用する
b) の場合は、解析時の加力方向を45°にした場合などに用いる検討になります。
その他、通常のX,Y方向加力でも直交方向応力の確認をしたい場合などに使用する事ができます。
なお、採用軸力は各方向加力の最大圧縮軸力、最大引張軸力を採用します。
そのため、実際には加力方向による応力と対応しない軸力によって耐力を定め、安全側として評価することになります。
a) X,Y方向加力を組み合わせ、45°加力時の応力を作る
- X,Y方向加力時の長期を除いた水平荷重によるモーメントに対して1/√2倍したモーメントを合算します。
- 上下動係数を考慮した場合、上下動係数による増減倍率に応じて、長期モーメントも変動させます。
b) 解析された加力方向による応力をそのまま採用する
- 上下動係数を考慮した場合、上下動係数による増減倍率に応じて、長期モーメントも変動は行いません。
検討集計
柱関係の検討集計
柱関係の検討集計を行います。
大梁関係の検討集計
大梁関係の検討集計を行います。
ブレース関係の検討集計
ブレース関係の検討集計を行います。
耐震壁関係の検討集計
耐震壁関係の検討集計を行います。