履歴特性

逆行型

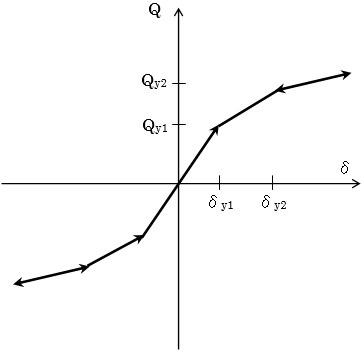
常にスケルトンカーブ上を進みます。

標準型

除荷履歴はMasing則（相似則）により決定されます。除荷開始時の剛性は初期剛性となり、除荷後の第2剛性、第3剛性は骨格曲線の剛性低下率と同様になります。

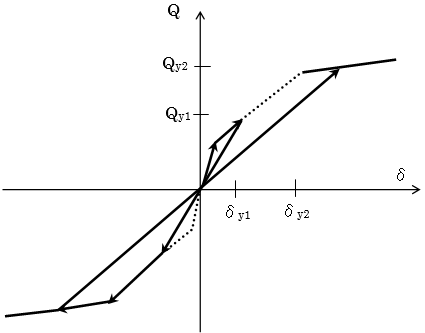
原点指向型

初期履歴ではスケルトンカーブ上を進み、その直線上から戻って反対方向に進むときは原点を通る直線上を進みます。

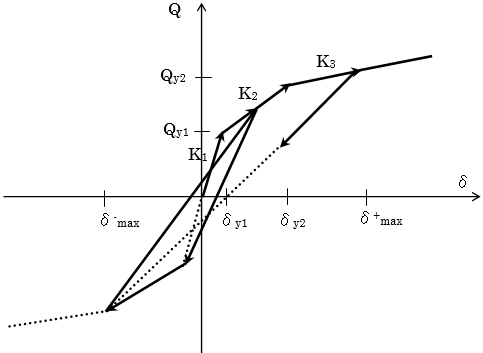
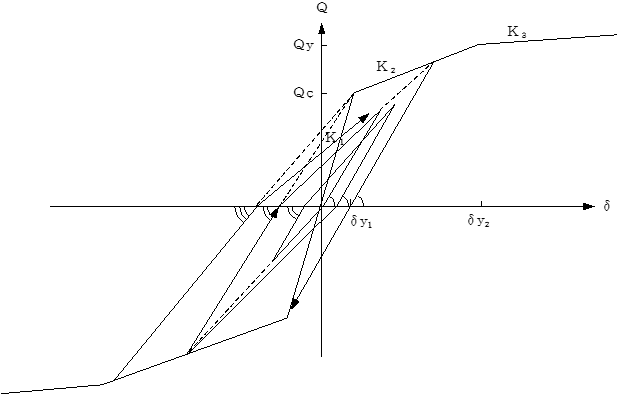
最大点指向型

(1) $|max|＜δ_{y1}$の場合は、原点を通る勾配 $K_1$の直線上を動きます。

(2) $δ$がはじめて $±δ_{y1}$または $±δ_{y2}$を超えた時点、あるいはこれまでの最大変形 $δ_{max}$を超えた時点で、スケルトンカーブ上の第2勾配 $K_2$または第3勾配 $K_3$の直線上を進みます。この直線上を戻って反対方向に進む場合は、戻り点から（この $δ$が新しく $δ_{max}$となる）反対側の、今までの最大変形点を目指します。

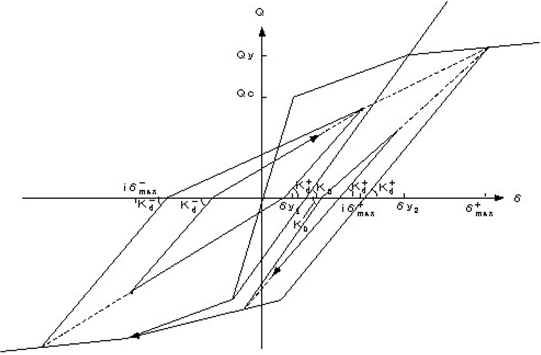
武田型

(1) $|max|＜δ_{y1}$の場合は、原点を通る勾配 $K_1$の直線上を動きます。

(2)
ⅰ) $δ$が $δ_{y1}$をこえた場合、スケルトンカーブ上の第2勾配 $K_2$の直線上を進みます。

ⅱ)この直線から戻って反対方向に進む場合は、戻り点（この $δ$が新しい $δ_{max}$となる）から反対側の第１折点を目指します。

$${K_d}^+ = K_0 \times \left| \frac{{\delta^+}_{max}}{\delta _{y2}} \right|^{-\nu}$$

ⅲ)反対側の最大変形が弾性域の場合は、この剛性域の範囲は反対側の第1折点までとします。

ⅳ)反対側の最大変形が $δ_{y1}$をこえている場合は、この剛性域の範囲は復元力が0となる点までとします。そして、この0点をこえた場合は、反対側の最大変形点を目指します。更に、この最大変形点を目指す直線から戻る場合以降の規則は、図を参照して下さい。

ⅴ)最大変形点をこえた場合は、スケルトンカーブ上の第2勾配 $K_2$の直線上を進みます。

(3)

ⅰ) $δ$が $δ_{y2}$をこえた場合、スケルトンカーブ上の第3勾配 $K_3$の直線上を進みます。

ⅱ)この直線上を戻って反対方向に進む場合は、戻り点（この $δ$が新しい $δ_{max}$となる）から、下式で求まる勾配 $K_d$の直線上を進みます。

ⅲ) 反対側の最大変形が $δ_{y1}$をこえていない場合は、勾配 $K_d$の範囲は反対側の $Q_c$までとします。更にこの $Q_c$をこえた場合は、第2折点を目指します。

ⅳ) 反対側の最大変形が $δ_{y1}$をこえている場合は、勾配 $K_d$の範囲は復元力0の点までとします。更にこの0の点をこえた場合は、最大変形点を目指します。ただし、反対側の最大変形が $δ_{y2}$をこえていない場合は第２折点を目指します。また、この場合は $δ_{max}＝δ_{y2}$となります。

ⅴ) ⅲ)において、第２折点を目指す直線上から戻る（この $δ$が新しい $δ_{max}$となる）場合は、勾配 $K_0$の直線上を進みます。更に復元力0の点をこえると、最大変形点を目指します。この最大変形点を目指す直線上から戻る場合は、上式で求まる勾配 $K_d$上を進み、復元力0をこえると、反対側の最大変形点を目指します。

ⅵ) ⅳ)において、最大変形点を目指す直線上から戻る（この $δ$が内部ループの最大変形 $_iδ_{max}$となる）場合は、勾配 $K_d$上を進み、復元力0の点をこえると、最大変形点を目指します。この最大変形点を目指す直線上から戻る（内部ループの反対側の最大変形 $_iδ_{max}$とする）場合も、勾配 $K_d$上を進み、復元力0の点をこえると内部ループの最大変形点を目指します。

ⅶ) ⅳ)において、内部ループの最大変形点をこえてスケルトンカーブ上の最大変形点に向かって動いている途中で、反対方向に進む場合は勾配 $K_d$上を進み、復元力0の点をこえると、反対側のスケルトンカーブ上の最大変形点を目指します。

【参考文献】

Takeda, Sozen and Nielsen : Reinforced Concrete Response to Simulated

Earthquakes, Journal, Structural Division, ASCE, Vol.96,No.ST12,1970

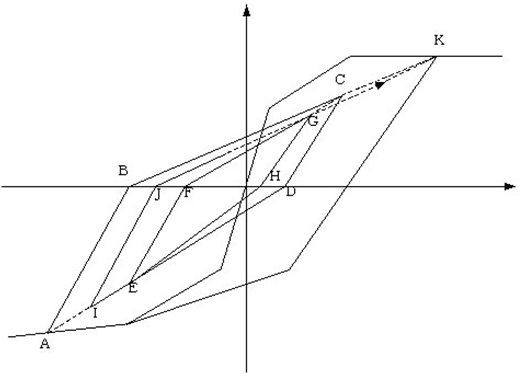
ⅶ)の説明図

A→B→…→Kと進みます。

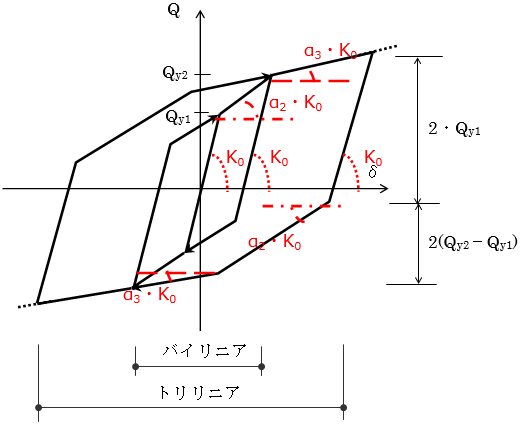
辻・山田モデル

辻・山田モデルのスケルトンは、バイリニアです。スケルトン情報以外に、辻・山田モデル用β値の設定を行う必要があります。辻・山田モデルは、以下に示す法則に従って動きます。

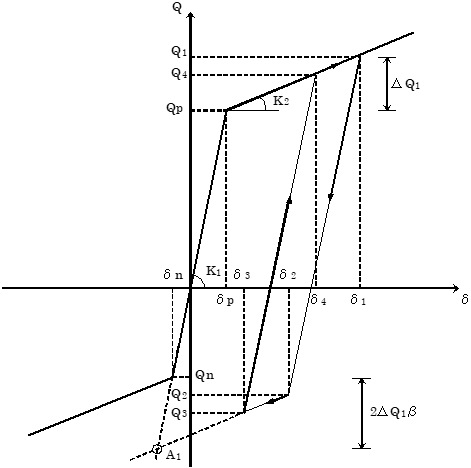
(1) $δ_n ≤ δ ≤ δ_p$の場合、原点を通る勾配 $K_1$の直線上を動きます。

(2) i) $δ$が $δ_n$および $δ_p$を越えた場合、勾配 $K_2$の直線上を進みます。

ii) この直線上の点（ $δ_1$, $Q_1$）から戻って反対方向に進む場合は、勾配 $K_1$で以下の点（ $δ_2$, $Q_2$）を目指します。（ $δ_2$, $Q_2$）は点 $A_1$を通る勾配 $K_2$の直線との交点です。

ここに $ΔQ_1$ ：等方硬化開始点と除荷点との耐力差

正側で初降伏の場合： $ΔQ_1=Q_1-Q_p$

負側で初降伏の場合： $ΔQ_1=Q_1-Q_n$

$β$ ：辻・山田モデル用 $β$値 $(0.0≦β≦1.0)$
$d$ ：変形
$d_p$ , $d_n$：降伏変形

iii) （ $δ_2$, $Q_2$）を目指している途中で反対方向に進む場合は、勾配 $K_1$で（ $δ_1$, $Q_1$）を目指し、（ $δ_1$, $Q_1$）に到達した場合、勾配 $K_2$の_直線上を進みます。

iv) （ $δ_2$, $Q_2$）に到達した場合、勾配 $K_2$の直線上を進みます。

(3)

i) 勾配 $K_2$を進行中、（ $δ_3$, $Q_3$）より反対方向に進む場合は、勾配 $K_1$で以下の点（ $δ_4$, $Q_4$）を目指します。（ $δ_4$, $Q_4$）は点 $A_2$通る勾配 $K_2$の直線との交点です。

ii)（ $δ_4$, $Q_4$）に達した後は、勾配 $K_2$で進みます。

【β値】

辻・山田モデル用 $β$値とは、移動硬化と等方硬化の割合を決定するパラメータです。

$\Delta \bar{\sigma} = \beta \left| \Delta \sigma \right|$ $\Delta \bar{ \alpha } = (1 - \beta) \left|\Delta \sigma \right|$

ここに、

$\Delta \sigma$：剛性変更点からの増分応力

$\Delta \bar{\sigma}$：等方硬化が負担した増分応力（降伏幅の膨張）

$\Delta \bar{\alpha}$：移動硬化が負担した増分応力（降伏幅中心の移動）

$β=1.0$の場合、剛性変更点から塑性化した応力分だけ降伏幅が膨張します。つまり、塑性化した符号の反対側の剛性変更点も同様の値となります。逆に、 $β=0.0$の場合、降伏幅の変更は起こらず、中心のみが移動するループを描く（耐力が正負同じ場合は、「標準型」と同様のループ）ようになります。

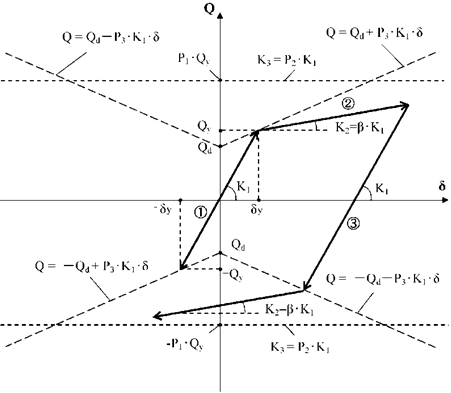
JFE LYトリリニア

履歴則を以下に示します。

(1) 基本ルール

1) $｜δmax｜＜δ_y$の場合、原点を通る勾配 $Ｋ_1$の直線上を動きます。

2) $δ$が初めて $±δ_y$を越えた場合は、第2勾配 $Ｋ_2$（＝ $β・K_1$）の直線上を進みます。

3) 2)の直線上を戻って反対側に進む場合は、戻り点から勾配 $K_1$にて進み、反対側の第2勾配を規定する直線（ $-Q_d$を通る勾配 $P_3・K_1$の直線）の交点まで進みます。折れ点以降は、第2勾配 $K_2$（＝ $β・K_1$）の直線上を進みます。

4) 3)の直線上を戻って、反対側に進む場合は、3)の規則を繰り返します。

注）現在プログラム内部において、 $P_2＝0$としている。

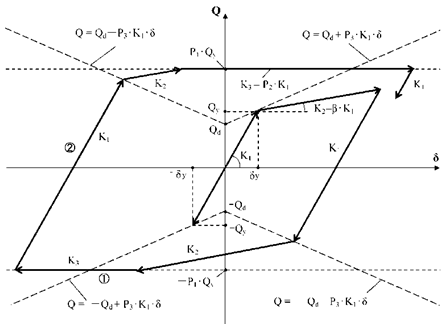
(2) 履歴ループが第3勾配の直線と交差した場合は、以下の基本ルールに従うものとします。

1) 第2勾配で進み、第3勾配の直線（図の一点波線内）を越えた場合、その直線上第3勾配 $K_3$（＝ $P_2・K_1$）の直線上を進みます。

2) 1)の直線上を戻って反対側に進む場合は、戻り点から勾配 $K_1$にて進み、反対側の第２勾配を規定する直線（ $-Q_d$を通る勾配 $P_2・K_1$の直線）の交点まで進みます。折れ点以降は、第２勾配 $K_2$（＝ $β・K_1$）の直線上を進みます。

3) 2)の直線上を戻って反対側に進む場合は、2)の規則を繰り返します。

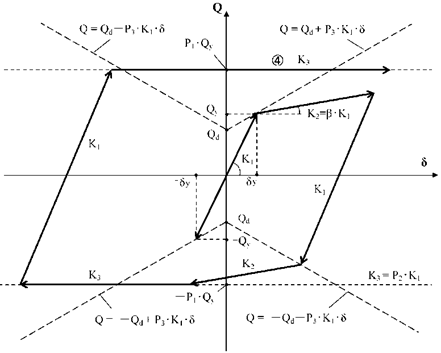
4) ただし、下図のように $Ｋ_1$で進む直線が、第２勾配を規定する直線と交差する前に第3勾配と交差する場合は、直接第3勾配で進みます。（次項図④の直線を参照）

注）現在プログラム内部において、 $P_2＝0$としている。