質点系解析モデルの非線形特性

復元力特性のモデル化（上部構造）

初期剛性

本プログラムでは、増分解析の最初のポイント（第１ステップ）の荷重－変形関係から初期剛性（K₁）を計算します。従って、荷重増分解析の第１ステップの状態で非線形領域に入ってしまう解析結果からは、初期剛性を正しく計算できません。特に、初期応力が過大なことによって発生する第１ステップでの剛性変更などには注意してください。

接線勾配

指定した位置（荷重ステップ間は線形補間）とその直前のポイント（荷重ステップ）を結ぶ勾配とします。

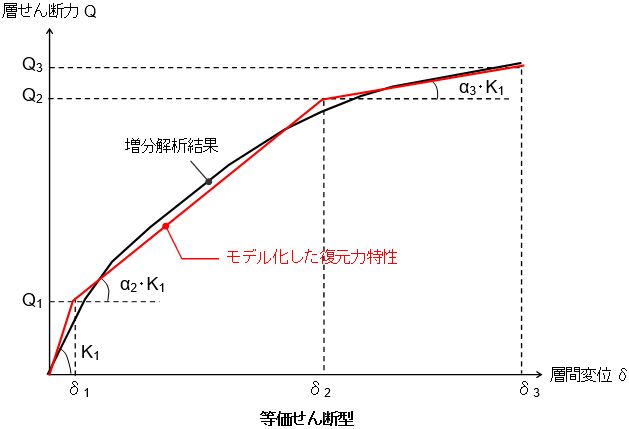
等価せん断型モデル・等価曲げせん断型モデル

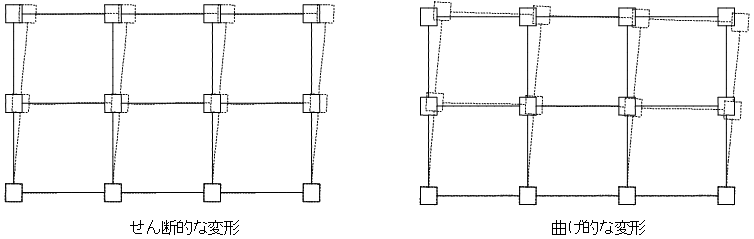
地震時の構造物の変形は、せん断的な変形（下左図）と曲げ的な変形（下右図）の組み合わさったものであると考えることができます。本プログラムでは、「等価せん断型モデル（全て非線形のせん断型成分であると仮定するモデル）」と、「等価曲げせん断型モデル（弾性の曲げ成分と非線形のせん断成分の組み合わせであると仮定するモデル）」の２つの考え方によるモデル化を行うことができます。

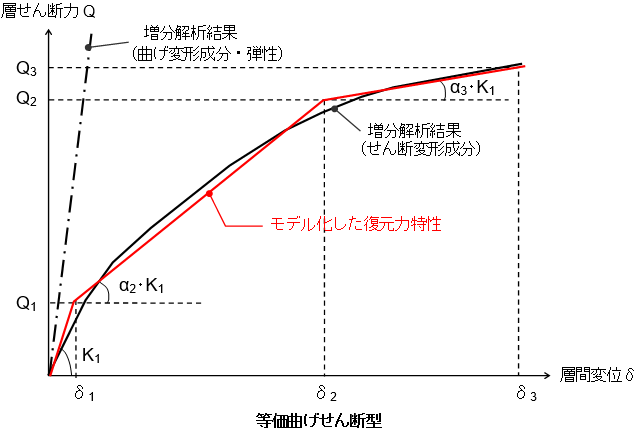
節点の鉛直変位から曲げ剛性を計算（曲げ剛性の直接入力では入力値を使用）し、曲げ変形成分を計算し、これを全体の層間変位から差し引いた残りをせん断変形成分とします。

ここで、

$K_1$：初期剛性

$α_2$・ $K_1$：第２剛性

$α_3$・ $K_1$：第３剛性

$Q_1,δ_1$：第1折点のせん断力，変位

$Q_2$, $δ_2$：第2折点のせん断力，変位

$Q_3$, $δ_3$：第3折点のせん断力，変位

本プログラムでは、第１折点および第３折点を指定し、第２折点を自動計算する方法（ルール１、２）と、第２折点および第３折点を指定し第１点を自動計算する方法（ルール３）があります。

ルール１、２による自動計算では、第３折点までの包絡面積がスケルトンカーブの包絡面積と等しくなるように、第２折点を設定します。また、第３勾配は第３折点の接線勾配とします。

ルール１では、第１折点はQ-δ曲線において割線剛性が初期剛性に対して指定値以下となった時点の変位により第１折点を決定します。

ルール２では、各階において最初に降伏部材が発生した時点の変位に対する比率を指定します。指定値に相当する変位を超えた時点の変位により第１折点を決定します。

ルール３による自動計算では、第２折点までの包絡面積がスケルトンカーブの包絡面積と等しくなるように、第１折点を設定します。また、第３勾配は第３折点の接線勾配とします。降伏ヒンジが発生した大梁端部の比率が指定値を超えた時点の変位により第２折点を決定します。

等価曲げ剛性の計算方法

第１ステップに関する柱の鉛直方向変位と柱軸力からひずみエネルギーの和が等しくなるような平面保持型の $_eθ_i$を求め、これに対応する等価曲げ剛性 $_eEI_i$を計算します。

i階での増分回転角を $_eθ_i$とすると、下式が成立するものとします。

$$ \sum_{j=1}^{n} \left( {}_{j}N_i・{}_j \Delta V_{i} \right) = \sum_{j=1}^n \left( {}_jN_i\left({}_e \Delta \theta_i・{}_jL_i \right) \right) $$

したがって、

$$ e\Delta \theta_i = \frac{\sum_{j=1}^{n} N_i (_{j}N_i \cdot _j\Delta V_i )}{\sum_{j=1}^{n} (_{j}N_i \cdot _jL_{i} )} $$

ここで、

$_jN_i$ : i階j軸の鉛直部材（柱、ブレース、壁、支持バネ）軸力 ※ブレースは指定により除外可。

$_jΔV_i$ : i層j軸の柱の鉛直方向変形

$_jL_i$ : i階j軸の柱の中立軸位置からの距離

等価曲げ剛性 $_eEI_i$は、モールの定理より

${}_e \Delta \theta _i = \int _{xi}^{xi+1} \frac{M_x}{EI_x} dx$

したがって、等価曲げ剛性 $_eEI_i$は次式で求められます。

$e EI_i = h_i \frac{M_{i+1}+M_i}{2・{}_e \Delta \theta _i}$

曲げ変形成分 $_bδ_i$は、下式で求められます。

$b \delta_i = {h_i}^2 \frac{2 \cdot M_i+M_{i+1}}{6 \cdot {}_e EI_i}$

せん断変形成分 $_Sδ_i$は、下式で求められます（ $δ_i$はi層の全体変形）。

${}_S \delta _i = \delta _i - {}_b \delta _i - \sum _{j=1}^{i-1} h_i・{}_e \Delta \theta _j$

よって等価せん断剛性は次式で求められます。

${}_eGA_i = Q_i・\frac{h_i}{{}_s \delta _i}$

中立軸位置の自動計算方法

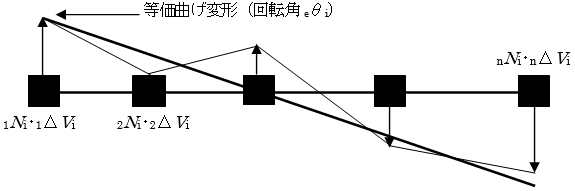
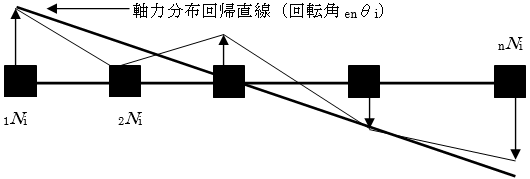
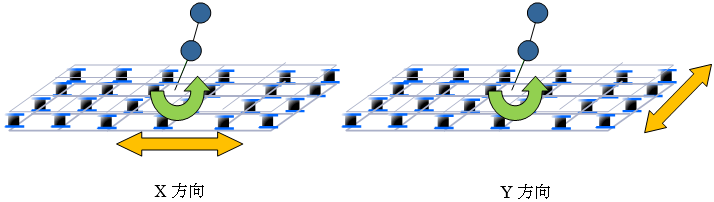
下図に示した各層軸力jNiを用いて、軸力分布回帰直線の回転角と中立軸位置を求めています。

下式が最小となる直線を最小二乗法によって求め、軸力分布回帰直線としています。

$$ \sum _{j=1}^n \left({}_jN_i-{}_jL_i \cdot _{en}\theta _i \right)^2 $$

ここで、

$_jN_i$ : i層j軸の鉛直部材（柱、ブレース、壁、支持バネ）軸力

$_jL_i$ : i層j軸の柱の中立軸位置からの距離

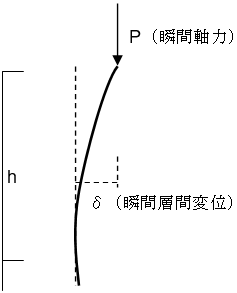
P－δ効果の評価方法（免震支承材）

鉛直支持材（柱・ブレース・壁など）の瞬間鉛直支持軸力と、各位置での瞬間層間変位を乗じて、P－δ効果による瞬間付加モーメント（ $⊿M$）を算出します。指定されたフレームに含まれる全ての鉛直支持材についての瞬間付加モーメントの総和（ $Σ⊿M$）を求め、Σ⊿Mを階高（ $h$）で除して求めた層せん断力（ $⊿Q$）をＰ－δ効果による層せん断力の低下とします。 $⊿Q$の計算は、Q－δ曲線の全ステップ分を逐次計算します。下図に示した各層軸力 $_jN_i$を用いて、軸力分布回帰直線の回転角と中立軸位置を求めています。免震支承材の場合、三山モデルを採用します。

$⊿M=P×δ$
$⊿Q=(Σ⊿M)/h$

質点系解析モデル

共通条件

Ｘ，Ｙ方向別々のモデルとしてモデル化されます。
上下方向の自由度は拘束します。

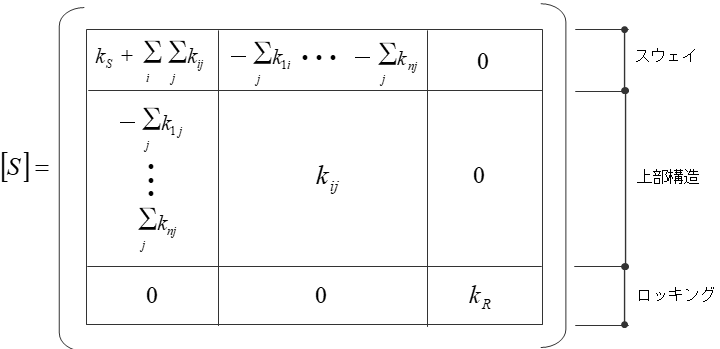
剛性マトリクス

スウェイ・ロッキングを考慮した剛性マトリクスは、以下のように表されます。

ここで、

$[S]$：剛性マトリクス　

$k_{ji}$：上部構造の剛性マトリクスの要素

$k_s$：スウェイのバネ定数

$k_R$：ロッキングのバネ定数

質量マトリクス

スウェイ・ロッキングを考慮した質量マトリクスは、以下のように表されます。

ここで、 $[M]$：質量マトリクス

$m_i$：i層の質量

$m_s$：基礎の質量

$m_r$：ロッキング質量慣性モーメント

$h_i$：i層の基礎からの高さ

モデル化タイプ

　モデル化タイプは下記の３つから選択可能です。

等価せん断型

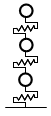
曲げ剛性を剛とします。（曲げ変形０）
剛床内並列ばねが設定できます。
一般的に塔状比の小さい建物で適用します。塔状比が大きい建物に適用した場合、立体モデルと高次モードの性状に差が生じてきます。

等価曲げせん断型

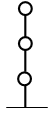
曲げ剛性を梁要素として考慮します。
剛床内並列ばねが設定できます。（Ver.2.8.0.4～）
一般的に塔状比の大きい建物で適用します。
速度依存ダンパーは曲げ変形を含んだ変形に対して作用します。

曲げせん断分離型

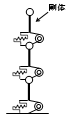
曲げ剛性を回転ばねとして考慮します。
剛床内並列ばねが設定できます。
一般的に塔状比の大きい建物で適用します。
モデル化が異なるため、等価曲げせん断型と固有周期に若干差が生じます。（概ね1%程度）
速度依存ダンパーをせん断変形のみに作用させることができます。

ダンパーのモデル化

ダンパーは履歴型、速度依存型によってそれぞれ下記のように選択できます。

履歴型ダンパーの場合

1．ダンパーを個別にモデル化する場合（付加ばねを介して質点間に接続）

各層ごとの保有付加剛性を設定するか、状態N,R,T解析から算出される保有付加剛性をダンパーごとに接続する方法があります。計算方法は保有付加剛性の計算方法をご参照ください。

2．Q-δ曲線上で分離する場合（直接質点間に接続）

静的荷重増分解析結果を元に、各ステップにおいて各階ダンパー負担せん断力-各階層間変位関係を取得します。
この層せん断力-変形関係を元に、ダンパー部の骨格曲線をトリリニアとしてモデル化します。

速度依存型ダンパーの場合

1．保有付加剛性を考慮する場合（付加ばねを介して質点間に接続）

履歴型ダンパーと同様です。

　　　※付加ばねに曲げ変形分が考慮されていると考え、減衰要素は付加ばねを介して質点間に配置します。

2．保有付加剛性を考慮しない場合（直接質点間に接続）

　　　※曲げせん断分離型の場合、減衰要素はせん断変形にのみ作用します。

保有付加剛性の計算方法

各階ごとの保有付加剛性を算出する場合

各層保有付加剛性は以下の計算により算出します。

$K'_i = Q_i * (1 / \delta_R - 1 / \delta_N)$

ダンパーごとの保有付加剛性を算出する場合

状態RまたはT解析によるダンパーの有効剛性に対し、状態Nによる実効変形比を考慮して付加剛性を算出します。

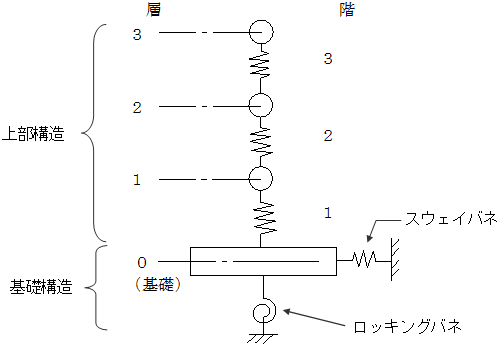
スウェイ・ロッキングモデル

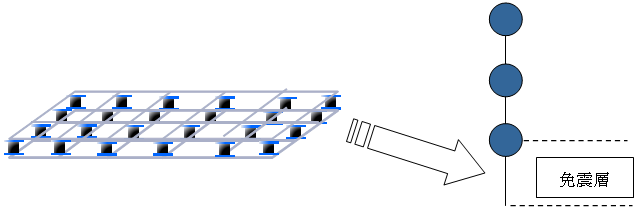
質点系解析モデルは、層・階で認識される上部構造と、その下の基礎構造により構成されます。解析モデルは、層ごとに水平方向の振動自由度をもち、基礎はロッキング（基礎回転）とスウェイ（基礎移動）の２自由度を考慮できます。

上部構造の非線形特性は、増分解析結果からモデル化した復元力特性により評価します。基礎構造については、ロッキング・スウェイを入力値（ロッキング用重量慣性モーメント・ロッキングのバネ定数・ロッキングの減衰定数、スウェイ用重量・スウェイのバネ定数・スウェイの減衰係数）により評価します。

免震考慮モデル（免震層ねじれ考慮無し）の場合

免震考慮モデル（免震層ねじれ考慮無し）の場合は免震層については上部構造と同一のＸＹ座標に対して集中配置されます（Ver.2.8.0.0よりモデル化を変更しました）。免震層の曲げ剛性は、上部構造の曲げせん断型の曲げ剛性と同様の方法で計算して考慮されます。上部構造については耐震モデルと同様にモデル化されます。免震層上下節点の自由度は並進方向、X軸回りおよびY軸回り回転をフリーとし、鉛直および回転自由度は拘束します。本モデルの場合は、スウェイ・ロッキングを考慮することができます。

免震考慮モデル（免震層ねじれ考慮、上部ねじれ非考慮）の場合

免震考慮モデル（免震層ねじれ考慮、上部ねじれ非考慮）の場合は免震層については立体的に配置され、上部構造については串団子モデルとしてモデル化されます。免震層上下節点の自由度は並進方向およびねじれ方向をフリーとし、X軸回りおよびY軸回りの回転自由度は拘束します。上部構造の各質点には並進質量の他に回転慣性質量が考慮されます。上部構造のねじれ剛性は剛としてモデル化します。本モデルで免震層のねじれの検討を行う際には以下の点に注意が必要です。

・質点系モデルを配置する座標を適切に設定する必要があります。免震層の一つ上の階のせん断力重心（軸力重心）に配置するのが望ましいです。

・本モデルでは免震層のねじれは精度よくモデル化できる可能性がありますが、上部構造の応答評価には適切でない場合があります。串団子モデルは原則的にねじれが生じない建物に対して行うモデル化であり、上部構造にねじれが生じる場合にはそのままでは精度よくモデル化できないことがあります。

・本モデルの場合は、スウェイ・ロッキングを考慮することができません。