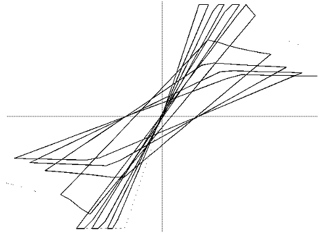
立体解析モデルの非線形特性
立体解析モデルの非線形特性
立体解析モデルの動的解析のための既定の非線形特性を部材、構造種別ごとに下表に示します。
| 部材種別 | 成分 | RC造・SRC造・CFT造 | S造 |
|---|---|---|---|
| 梁 | 曲げ | 武田型(トリリニア) | 標準型(バイリニア) |
| 軸方向 | 弾性 | 弾性 | |
| せん断 | 弾性 | 弾性 | |
| 柱 | 曲げ | ファイバーモデル*1 | ファイバーモデル*1 |
| 軸方向 | ファイバーモデル*1 | ファイバーモデル*1 | |
| せん断 | 弾性 | 弾性 | |
| 耐震壁 | 曲げ | ファイバーモデル | ― |
| 軸方向 | ファイバーモデル | ― | |
| せん断 | 原点指向型(トリリニア) | ― | |
| ブレース | 曲げ | ― | ― |
| 軸方向 | ― | 標準型(バイリニア)*2 | |
| せん断 | ― | ― |
*1:ファイバーモデルでは、鉄筋・鉄骨:標準型バイリニア、コンクリート:NewRCモデル(原点指向型)としてモデル化しています(ただし、NewRCの適用範囲であるFc60を超える強度、もしくはユーザー定義コンクリートの場合はBilinearの骨格曲線に対する原点指向型となります。適用範囲外のため、関数の形状が異常となるためです。)。また、指定により弾性とすることが可能です。
*2:指定により、非線形特性を個別に設定することが可能です。
鉄骨大梁の座屈を考慮した履歴
指定により、鉄骨大梁の座屈を考慮した履歴則を採用する事ができます。
座屈形式に応じて、以下の履歴則を採用します。
局部座屈
文献「加藤・秋山・帯: 局部座屈を伴うH形断面部材の変形, 日本建築学会論文報告集 第257号・昭和52年7月」を元に履歴則を設定します。
除荷特性は文献「孟・大井・高梨: 鉄骨骨組地震応答解析のための耐力劣化を伴う簡易部材モデル, 日本建築学会構造系論文報告集 第437号・1992年7月」によるROモデルを用います。
ROモデルの諸元は、γ=5, Φ=0.5とします。
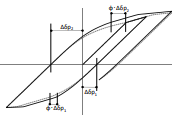
横座屈
文献「井戸田・中田・吉田・小野: 横座屈で耐力が決まるH形鋼梁の繰返し履歴モデル,?日本建築学会構造系論文集?第80巻?第711号 819-829 2015年5月」を元に履歴則を設定します。
最大曲げ耐力 $M_u$ は以下のように計算します。
$$ \frac{\mu_{Mu}}{M_p}=\frac{2h_0}{1+c_{def}\lambda_b+(1+c_{res})\lambda_b^2+\sqrt{(1+c_{def}\lambda_b+(1+c_{res})\lambda_b^2)^2-4\lambda_b^2(1+c_{res}\lambda_b^2)}} $$ここで、
$c_{res}$ : 残留応力度の大きさを考慮する係数(=0.0)
$c_{def}$ : 初期たわみ量の大きさを考慮する係数(=
$q_{\kappa}k_{def}^r$)
$h_0$ : 塑性化後の歪み硬化による耐力上昇率
$f$ : 形状係数(=1.0)
$k_{res}$ : 降伏応力度に対する最大残留応力度の大きさの比率(=0.3)
$k_{def}$ : 部材初期たわみ量の正弦波成分の最大振幅を
$k_{def}・l_b/1000$ で表したときの係数(=1.0)
$\Lambda_c'$ : 基準化幅厚比と弾性限界細長比を用いて定義される変形性能指標(=
$( \lambda_b / _e\lambda_b + WF^3)^{1/3}$)
$h_0=\alpha_{\Lambda_c'}(\Lambda_c'-1.25)+1.0$ …
$(\Lambda_c'\leq1.25)$
$h_0=1.0$ …
$(\Lambda_c'\gt1.25)$
$q_{\kappa}=-0.1\kappa+0.065$ …
$(-1.0\leq\kappa\leq0.0)$
$q_{\kappa}=0.065$ …
$(0.0<\kappa)$
$r=0.5\kappa+1.0$ …
$(-1.0\leq\kappa\leq0.0)$
$r=1.0$ …
$(0.0<\kappa)$
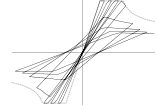
連成座屈
文献「大谷・井戸田: 局部座屈と横座屈を考慮したH形鋼梁の繰返し履歴モデル, 日本建築学会構造系論文集 第84巻 第765号 1475-1484 2019年11月」を元に履歴則を設定します。
最大耐力
$M_u$ は、横座屈と同様に算出します。
耐力劣化の開始点は、論文中の
$\theta_{static}$ を採用します。