鉄筋コンクリート柱の終局耐力
鉄筋コンクリート造柱の終局耐力
柱検定表の符号一覧
鉄筋コンクリート造柱の終局検定表の符号一覧を以下に示します。
[塑性理論式]
$B$:柱幅(mm)
$D$:柱せい(mm)
$d_t$:引張縁から引張鉄筋重心までの距離(mm)
$a_t$:引張鉄筋の断面積(mm2)
$L$ : 部材長、内法(mm)
$p_t$:引張鉄筋比(%)
$p_w$:せん断補強筋比(%)
$p_g$:主筋全断面積のコンクリート全断面積に対する比(%)
$M_{m1}$:正加力時の終局曲げ応力(kN・m)
$M_{m2}$:負加力時の終局曲げ応力(kN・m)
$M_{u1}$:正加力時の終局曲げ強度(kN・m)
$M_{u2}$:負加力時の終局曲げ強度(kN・m)
$Q_{m1}$:正加力時の終局せん断応力(kN)
$Q_{m2}$:負加力時の終局せん断応力(kN)
$Q_{su}$:せん断破壊によって決定するせん断耐力(kN)
$Q_{bu}$:付着割裂破壊によって決定するせん断耐力(kN)
$N_L$:長期柱軸力(kN)
$N_{m1}$:正加力時の終局時柱軸力(kN)
$N_{m2}$:負加力時の終局時柱軸力(kN)
$N_{ut}$:軸圧縮強度(kN)
$N_{uc}$:軸引張強度(kN) [靭性指針式]
$B$:柱幅(mm)
$D$:柱せい(mm)
$d_t$:引張縁から引張鉄筋重心までの距離(mm)
$a_t$:引張鉄筋の断面積(mm2)
$p_t$:引張鉄筋比(%)
$p_g$:主筋全断面積のコンクリート全断面積に対する比(%)
内法(mm)
$j_e$:トラス機構に関与する断面の有効せい(mm)
$b_e$:トラス機構に関与する断面の有効幅(mm)
$μ$:トラス機構の角度を表す係数( $=2-20R_p$)
$R_p$:終局限界状態でのヒンジ領域の回転角(rad)
$ν$:コンクリート圧縮強度の有効係数 $\left( =(1-20R_p)ν0 \right) $
$ν_0$:降伏ヒンジ・潜在ヒンジを計画しない時の有効係数 $\left( =0.7- \frac{σ_B}{200}\right)$
$σ_B$:コンクリートの圧縮強度(N/mm2)
$p_{we}$:有効横補強筋比(%)( $=a_w/b_{es}$)
$a_w$:1組の横補強筋の断面積(mm2)
$s$:横補強筋の間隔(mm)
$M_{m1}$:正加力時の終局曲げ応力(kN・m)
$M_{m2}$:負加力時の終局曲げ応力(kN・m)
$M_{u1}$:正加力時の終局曲げ強度(kN・m)
$M_{u2}$:負加力時の終局曲げ強度(kN・m)
$Q_L$:長期せん断応力(kN)
$Q$:両端ヒンジ時せん断力もしくは長期を除いた設計用せん断力
$V_{u1}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.1)の値(kN)
$V_{u2}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.2)の値(kN)
$V_{u3}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.3)の値(kN)
$V_{u}$せん断信頼強度( $=min(V_{u1}, V_{u2}, V_{u3})$) (kN)
$τ_{bu}$:1段目主筋の付着信頼強度(N/mm2)
$τ_f$:1段目主筋の設計用付着応力度(N/mm2)
$τ_{bu}$:2段目主筋の付着信頼強度(N/mm2)
$τ_{f2}$:2段目主筋の設計用付着応力度(N/mm2)
$V_{bu}$:付着破壊の影響を考慮したせん断信頼強度(kN)
$N_L$:長期柱軸力(kN)
$N_{m1}$:正加力時の終局時柱軸力(kN)
$N_{m2}$:負加力時の終局時柱軸力(kN)
$N_{ut}$:軸圧縮強度(kN)
$N_{uc}$:軸引張強度(kN)
OTM低減:応答転倒モーメントの低減係数
上下動係数:上下動を考慮した軸力の割増係数
鉄筋コンクリート造柱の終局検定においては、5章の非線形解析モデルによる荷重増分解析結果に対し、以降に示す終局耐力を用いて検定を行います。実際の解析時における曲げ復元力特性は5章の非線形解析モデルによるモデル化が採用され、下記の終局曲げ強度と必ずしも一致しないことにご注意ください。
a) 終局曲げ強度( $M_u$)
鉄筋コンクリート造柱の終局曲げ強度( $M_u$)は、引張側と圧縮側に各1段の主筋を配筋した略算式である、構造規定式(at式)1)またはACI規準による平面保持解析にて算定します。寄筋がある場合、寄筋も $at$に含んで計算します。
・構造規定式(at式)
$M_u = 0.8 \cdot a_t \cdot \sigma_y \cdot D+0.4 \cdot N \cdot D$
$M_u = 0.8 \cdot a_t \cdot \sigma_y \cdot D+0.5 \cdot N \cdot D \left( 1-\frac{N}{b \cdot D \cdot F_c} \right)$
$M_u = (0.8 \cdot a_t \cdot \sigma_y \cdot D+0.12 \cdot b \cdot D^2 \cdot F_c) \cdot \left( \frac{N_{\max}-N}{N_{\max}-0.4 \cdot b \cdot D \cdot F_c} \right)$
$N_{max}$:中心圧縮時終局強度( $-b・D・F_c+a_g・σ_y$)(N)
$N_{min}$:中心引張時終局強度( $-a_g・σ_y$)(N)
$a_g$:主筋全断面積(mm2)
$N$:軸方向力(N)
$a_t$:引張主筋断面積(mm2)
$b$:柱幅(mm)
$D$:柱せい(mm)
$σ_y$:主筋降伏強度(N/mm2)
$F_c$:コンクリートの設計基準強度(N/mm2)
・ACI規準(平面保持仮定)
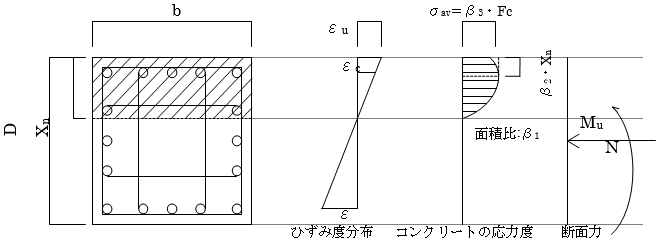
降伏曲げモーメントは、圧縮側コンクリートの応力分布を「ACI318-95規準」による等価応力度ブロック法を用いて、下記の①~⑥の仮定に基づいて算出します。
① 降伏曲げモーメントは圧縮縁のコンクリートのひずみ度が終局ひずみ $ε_u=0.3%$に達するときの曲げモーメントとする。
② 断面内各点のひずみ度は、中立軸からの距離に比例する。(平面保持の仮定)
③ 鉄筋の応力-ひずみ度関係は、降伏ひずみ度以下では弾性とする。降伏ひずみ度以上では材料強度とする。
④ コンクリートは引張応力度を負担しない。
⑤ コンクリートの圧縮応力度とひずみ度の関係は下図による。
⑥ 各係数は以下による
$ β_1 = \begin{align} \left\lbrace \begin{array}{ll} 0.85 & \displaystyle \left( F_c \leq 4000 \psi \right) \\ 0.85-0.05・(Fc-4000)/1000 & \displaystyle \left( 4000 \psi < F_c < 8000 \psi \right) \\ 0.65 & \displaystyle \left( 8000 \psi \leq F_c \right) \end{array} \right. \end{align} $
$β_2=β1/2$
$β_3=0.85$
$ ※1 (N/mm^2) \rightarrow 145.04 psi$
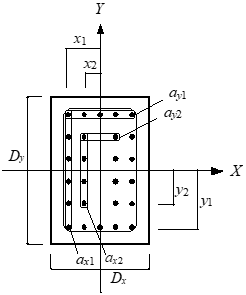
矩形柱の主筋の配置は次のように認識します。
$x_i, y_i$:図心からの各鉄筋重心位置
$a_{xi}, a_{yi}$:各鉄筋断面積
$i=1$ :1段引張主筋
$i=2$ :2段引張主筋
1) 国土交通省:2007年版建築物の構造関係技術基準解説書;P.626-627, 2007.8
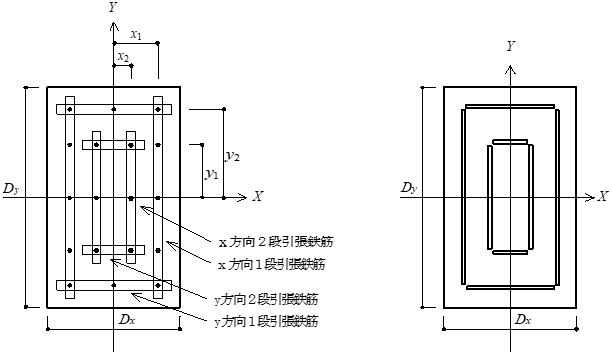
■隅部の鉄筋本数( $_{ck}N_i$)
$_{ck}N_i = \frac{2 \cdot (_{xk}n_i+ _{yk}n_i) - _{gk}N_i}{4}$
■引張鉄筋断面積( $_{jk}A$)
$_{jk}A = _{jk}a_1 \cdot _{jk}n_1 + _{jk}a_2 \cdot _{jk}n_2$
■鉄筋強度( $_{jk}Y$)
$_{jk}Y = ( _{jk} \sigma_{y1} \cdot _{jk}a_1 \cdot _{jk}n_1+_{jk}\sigma_{y2} \cdot _{jk}a_2 \cdot _{jk}n_2 )/_{jk}A$
$_{gk}N_i$:全鉄筋本数
$_{jk}a_i$:1本あたりの鉄筋断面積(mm2)
$_{jk}n_i$:鉄筋本数
$_{jk}σ_y$:鉄筋の降伏強度(N/mm2)
$i$:鉄筋径種類(i=1,2)
$j$:配置方向(j=X,Y)
$k$:1段筋または2段筋
b) 終局せん断強度( $Q_u$)
鉄筋コンクリート造柱の終局せん断強度( $Q_u$)は、鉄筋コンクリート造梁と同様に算定します(“採用応力"参照)。
鉄筋コンクリート造柱の余裕度は以下の様に計算しています。
$Q_{su}/Q_{mu} = \min (Q_{su}/Q_{mu1},Q_{su}/Q_{mu2})$
$Q_{bu}/Q_{mu} = \min (Q_{bu}/Q_{mu1},Q_{bu}/Q_{mu2})$
また、 $Q_D$と $Q_{mu}$については下記の違いがあります。
$Q_D = Q_L+a \times Q_E$
両端ヒンジを選択している場合: $Q_{mu}=(上限強度倍率)×(M_{iu}+M_{ju})/L$
存在応力を選択している場合: $Q_{mu}=Q_{L}+α×Q_{E}$
$M_{iu}$: 始端終局モーメント
$M_{ju}$: 終端終局モーメント
$Q_{mu}$: 両端ヒンジのせん断力
$L$: 危険断面位置間距離
c) 軸引張強度( $N_{ut}$),軸圧縮強度( $N_{uc}$)
鉄筋コンクリート造柱の軸圧縮強度( $N_{uc}$)、軸引張強度( $N_{ut}$)は構造規定2)に準じて算定します。本プログラムでは、圧縮軸力を正、引張軸力を負と表します。
$N_{uc} = b \cdot D \cdot F_c$
$N_{ut} = -a_g \cdot \sigma_y$
$N_{uc}$:軸圧縮強度(kN)
$N_{ut}$:軸引張強度(kN)
軸力に対する検定値は、以下のとおり算定します。OTM低減係数、上下動係数はユーザー指定によります。
スラブ筋断面積は「設計・計算条件」→「部材復元力特性条件」→「RC造大梁曲げ耐力計算方法」の設定を採用し、材料は「使用材料」→「その他」→「スラブ筋」の情報を採用します。
■長期軸力に対する検定
$N_L = N_{uc}$
■終局時軸力に対する検定
・ $min(N_{m1}$, $N_{m2})<0$または $max(N_{m1}$, $N_{m2})<0$の場合
$N_m / N_{ut}$
$N_m$:設計用柱軸力( $=min(N_{m1}, N_{m2})$または $max(N_{m1},N_{m2})$)(kN)
・ $min(N_{m1}, N_{m2})≧0$または $max(N_{m1},N_{m2})≧0$の場合
$N_m / N_{uc}$
$N_m$:設計用柱軸力( $=min(N_{m1}, N_{m2})$または $max(N_{m1}, N_{m2})$)(kN)
$N_m = N_L+|N_E| \cdot OTM \mbox{低減}+N_L \cdot \mbox{上下動係数}$
$N_L$:長期柱軸力(kN)
$N_{m1}$:正加力時の設計用柱軸力(kN)
$N_{m2}$:負加力時の設計用柱軸力(kN)
$N_E$:終局時柱軸力(kN)
国土交通省:2007年版建築物の構造関係技術基準解説書;P.626-627,629-630, 2007.8
注1) 「設計・計算条件」→「増分解析条件」→「部材耐力式・終局検定設定」参照。