鉄筋コンクリート梁の終局耐力
鉄筋コンクリート造梁の終局耐力
大梁検定表の符号一覧
鉄筋コンクリート造の大梁終局検定表の符号一覧を以下に示します。
[塑性理論式]
$B$:梁幅(mm)
$D$:梁せい(mm)
$_t$:引張縁から引張鉄筋重心までの距離(mm)
$L$ : 部材長,内法長さ(mm)
$a_t$:引張鉄筋の断面積(mm2)
$j_t$ : 応力中心間距離
$p_t$:引張鉄筋比(%)
$p_w$:せん断補強筋比(%)
$M_u$:終局曲げ強度(kN・m)
$Q_{mu}$:両端ヒンジを仮定した場合の終局せん断応力(kN)
$= \frac{\left( M_{u \textup{上}}+M_{u \textup{下}} \right) × \textup{上限強度倍率}}{ \textup{部材長(内法)}}$
$Q_L$:長期せん断応力(kN)
$Q_E$:水平荷重時せん断応力(kN)
$α$:せん断力割増率、ユーザー指定によります注1)。
$Q_{su}$:せん断破壊によって決定するせん断耐力(kN)
$α_{su}$:せん断に対する検定値(= $Q_{su}/Q_D$)
$Q_{bu}$:付着割裂破壊によって決定するせん断耐力(N)
$α_{bu}$:付着に対する検定値(= $Q_{bu}/Q_D$)
$τ_{bu}$:1段目主筋の付着信頼強度(N/mm2)
$τ_f$:設計用付着応力度(N/mm2)
$α_t$:梁の上端筋に対する付着強度低減係数
$b_{si2}$:2段目の割裂長さ比
$k_{st2}$:2段目主筋に対する横補強筋効果
$τ_{bu2}$:2段目主筋の付着信頼強度(N/mm2)
$L_d$:必要付着長さ(mm)
注1) 「設計・計算条件」→「増分解析条件」→「部材耐力式・終局検定設定」参照。
[靭性指針式]
$B$:梁幅(mm)
$D$:梁せい(mm)
$d_t$:引張縁から引張鉄筋重心までの距離(mm)
$L$ : 部材長,内法(mm)
$σ_y$:主筋の信頼強度算定用強度(N/mm2), 鉄筋材料強度×信頼強度倍率
$σ_{yu}$:主筋の上限強度算定用強度(N/mm2), 鉄筋材料強度×上限強度倍率
$j_e$:トラス機構に関与する断面の有効せい(mm)
$b_e$:トラス機構に関与する断面の有効幅(mm)
$μ$:トラス機構の角度を表す係数( $=2-20R_p$)
$R_p$:終局限界状態でのヒンジ領域の回転角(rad)
$ν$:コンクリート圧縮強度の有効係数( $=(1-20R_p)ν_0$)
$ν_0$:降伏ヒンジ・潜在ヒンジを計画しない時の有効係数 $\left( =0.7-\frac{σ_B}{200}\right)$
$σ_B$:コンクリートの圧縮強度(N/mm2)
$p_{we}$:有効横補強筋比(%)( $=a_w/b_{es}$)
$a_w$:1組の横補強筋の断面積(mm2)
$s$:横補強筋の間隔(mm)
$tanθ$:アーチ機構の圧縮束の角度のタンジェント
$Q_L$:長期せん断応力(kN)
$Q$:両端ヒンジ時せん断力もしくは長期を除いた設計用せん断力
$V_{u1}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.1)の値(kN)
$V_{u2}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.2)の値(kN)
$V_{u3}$:鉄筋コンクリート造建物の靭性保証型耐震設計指針 (6.4.3)の値(kN)
$Vu$:せん断信頼強度( $=min(V_{u1}, V_{u2}, V_{u3})$)
$V_{bu}$:付着破壊の影響を考慮したせん断信頼強度(kN)
$k_{st}$:1段目主筋に対する横補強筋効果
$k_{st2}$:2段目主筋に対する横補強筋効果
$Δσ$:1段目主筋の終局限界状態における部材両端部の応力度の差(N/mm2)
$Δσ2$:2段目主筋の終局限界状態における部材両端部の応力度の差(N/mm2)
$τ_{bu}$:1段目主筋の付着信頼強度(N/mm2)
$τ_f$:1段目主筋の設計用付着応力度(N/mm2)
$τ_{bu2}$:2段目主筋の付着信頼強度(N/mm2)
$τ_{f2}$:2段目主筋の設計用付着応力度(N/mm2)
鉄筋コンクリート造梁の終局耐力
終局検定においては、非線形解析モデルによる荷重増分解析結果に対し、以降に示す終局耐力を用いて検定を行います。
a) 梁の曲げひび割れ強度( $M_c$)、曲げ終局強度( $M_u$)
鉄筋コンクリート造梁の曲げひび割れ強度( $M_c$)および曲げ終局強度( $M_u$)については、非線形解析モデル(「曲げひび割れ強度」、「曲げ終局強度」)を参照してください。
b) 梁の塑性理論式による終局せん断強度( $Q_u$)
「終局耐力条件」で「終局強度型設計指針」を選択した場合、鉄筋コンクリート造梁の終局せん断強度( $Q_u$)は、塑性理論式により算定します。
付着に対する設計では、付着強度の確保(付着信頼強度( $τ_{bu}$)>設計用付着応力度 ( $τ_f$)が原則ですが、部材の耐力、変形性能が損なわれない範囲であれば付着ひび割れの発生、付着すべりの増大あるいは付着応力度の低下は許容することができるとされています1)。
本プログラムでは、終局時のせん断力に対してせん断強度、変形性能が損なわれないことの確認として以下の検定を行い、付着に関する数値( $τ_{bu},τ_f$)は参考として表示します。
$(Q_{su}-Q_L)/a \cdot Q_E \geq 1.0 \quad or \quad (Q_{su}-Q_L)/Q_{mu} \geq 1.0 $ せん断に対する余裕率
$(Q_{bu}-Q_L)/a \cdot Q_E \geq 1.0 \quad or \quad (Q_{bu}-Q_L)/Q_{mu} \geq 1.0 $ 付着に対する余裕率
※MK785, SPR785, SPR685を使用した場合、 $Q_L=Q_0$と読み替えて計算します。
$$Q_{su} = b \cdot j_t \cdot p_w \cdot \sigma_{wy} \cdot \cot \phi+k_1 \cdot (1-k_2) \cdot b \cdot D \cdot \nu \cdot F_c$$$k_1 = \frac{\sqrt{(L/D)^2+1}-(L/D)}{2}$
$k_2 = \frac{2 \cdot p_w \cdot \sigma_{wy}}{\nu \cdot F_c}$
$ \nu = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle (1.0-15 \cdot R_p) \cdot \nu_0 & \left(0 < Rp \leq 0.05 \right) \\ \displaystyle 0.25 \cdot \nu_0 & \left( 0.05 < Rp \right) \end{array} \right. \end{align}$
$ν_0 = 0.7- \frac{F_c}{200}$
$ \cot \phi = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle 2.0-50 \cdot Rp & \left(0 < Rp \leq 0.02 \right) \\ \displaystyle 1.0 & \left( 0.02 < Rp \right) \end{array} \right. \end{align}$
$Q_{su}$:せん断破壊によって決定するせん断耐力(N)
$b$:部材幅(mm)
$j_t$:主筋の重心間距離(mm)
$p_w$:せん断補強筋比(小数)
$σ_{wy}$:せん断補強筋の降伏強度算定用強度(N/mm2)
$L$:内法長さ(mm)
$D$:部材せい(mm)
$F_c$:コンクリートの設計基準強度(N/mm2)
※ $k_2≦1.0$とします。
※ $p_w・σ_{wy}≦ν・F_c/2$とします。
※ $ν,p_w,σ_{wy}$は次項の表によります。 $p_w$で上限を超える場合は上限値とします。
1 ) (社)日本建築学会:鉄筋コンクリート造建物の靭性保証型耐震設計指針・同解説;P.177,1997.7
| 製品名 | σwy(N/mm2) | Pw | ν |
|---|---|---|---|
| ウルボン【SBPD1275/1420】 | $min(25・Fc,1275)$ | $~1.2%$ $(~0.8\%^{*1})$ | $0.7(1.0-F_c/140)$ |
| リバーボン1275【SBPDN1275/1420】 | $~1.2\%$ | ||
| ウルボン785【UB785】 | $min(25・Fc,785)$ | $0.7(0.7-F_c/200)$ | |
| リバーボン785【KW785】 | |||
| スミフープ、ストロングフープ、 デーフープ【KSS785】 | |||
| UHYフープ【SHD685】 | $min(25・Fc,685)$ | ||
| エヌエスハイデック685H【HDC685】 | $685$ | ||
| スーパーフープ【KH785】 | $25・F_c ・・・(F_c<27.4)$ $ 785 ・・・(27.4≦F_c)$ | ||
| パワーリング785【SPR785】 | $25・F_c$
$・・・(F_c<32.0)$ $785 ・・・(32.0≦F_c)$ | ||
| パワーリング685【SPR685】 | $min(25・Fc,685)$ | ||
| エムケーフープ785【MK785】 | $25・F_c$
$・・・(F_c<31.4)$ $785 ・・・(31.4≦F_c)$ | ||
*1:柱において $F_c 27(N/mm^2)$未満の場合。
$Q_{bu}$:付着割裂破壊によって決定するせん断耐力(N)
$Q_{bu} = j_t \cdot \tau_{bu} \cdot \sum \phi+k_1 \cdot (1-k_3) \cdot b \cdot D \cdot \nu \cdot F_c$
$k_3 = \frac{2 \cdot \tau_b \cdot \sum \phi}{b \cdot \nu \cdot F_c}$
$τ_{bu}$:1段目主筋の付着信頼強度(N/mm2)
| 商品名 | 計算式 |
|---|---|
| リバーボン785【KW785】 | $τ_{bu} = k_0 \cdot 0.313 \left( 0.307b_1+0.427+ \frac{24.9a_w \cdot h}{x \cdot N \cdot d_b} \right) \cdot \sqrt{F_c}$ |
| スミフープ、ストロングフープ、 デーフープ【KSS785】 | |
| UHYフープ【SHD685】 | |
| エヌエスハイデック685H【HDC685】 | |
| ウルボン【SBPD1275/1420】 | $τ_{bu} = k_0 \cdot \left( 0.0961b_1+0.134+ \frac{7.8a_w \cdot h}{x \cdot N \cdot d_b} \right) \cdot \sqrt{F_c}$ |
| リバーボン1275【SBPDN1275/1420】 | |
| ウルボン785【UB785】 | |
| スーパーフープ【KH785】 | |
| パワーリング785【SPR785】 | |
| パワーリング685【SPR685】 | |
| エムケーフープ785【MK785】 | |
| 異径鉄筋 | $τ_{bu} = a_t \cdot \left( (0.085b_1+0.10) \cdot \sqrt{F_c}+k_{st} \right)$ $a_t =\begin{align}\left\lbrace\begin{array}{ll}\displaystyle 0.75 - \frac{F_c}{400} & (梁の上端主筋) \\\displaystyle 1.0 & ( 上記以外)\end{array}\right.\end{align}$ $ k_{st} =\begin{align}\left\lbrace\begin{array}{ll}\displaystyle (54+45N_w/N_1)(b_{si}+1)p_w & \left(b_{ci} \geq b_{si} \right) \\ \displaystyle 140A_w/(d_bs) & \left( b_{ci} < b_{si}\right) \end{array} \right. \end{align} $ |
$Σφ$:引張鉄筋の周長和(2段筋,寄筋を含める)(mm)
$k_0$: $1.0$(梁)、 $1.22$(柱)
$a_w$:せん断補強筋の断面積(mm2)
$b_i$:割裂線長さ比 $(= \min (b_{vi},b_{ci},b_{si})$
$b_{vi} = \sqrt{3} \cdot \left( \frac{2 \cdot C_{\min}}{d_{b1}}+1 \right)$
$b_{ci} = \sqrt{2} \cdot \left( \frac{C_S+C_b}{d_{b1}}-1 \right)$
$b_{si} = \frac{b}{N \cdot d_{b1}}-1$
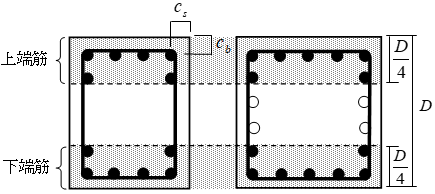
$C_{min}$:主筋のかぶり厚 $(=min(C_s,C_b))$(mm)
$C_s$:主筋の側面から側面までのかぶり厚さ(mm)
$C_b$:主筋の側面から底面までのかぶり厚さ(mm)
$d_{b1}$:1段目の主筋径(呼び名)(mm)
$h:b_i=b_{vi}$のとき $h = 0$
$b_i=b_{ci}$のとき $h = \sqrt{2}$
$b_i=b_{si}$のとき $h = 1.0+0.85 \cdot (n-2)/N$
$n$:1組のせん断補強筋の本数で、n>4の場合は4とします。
$x$:せん断補強筋ピッチ(mm)
$N$:外側一列の引張鉄筋の本数
2) (社)日本建築学会:鉄筋コンクリート造建物の靭性保証型耐震設計指針・同解説;P.175-181,1997.7
設計用付着応力度 $τ_f$、および2段目主筋の信頼強度 $τ_{bu2}$は、靭性指針2)に基づき算定します。
$\tau_f = d_b \cdot \Delta \sigma/(4 \cdot (L-d))$
$τ_f$:設計用付着応力度(N/mm2)
$⊿σ$:部材両端部の主筋の応力度の差。以下の計算により算出する。
$⊿σ= 2・σ_{yu}$ (両端ヒンジが発生している場合)
$⊿σ= σ_{yu}+σ_y$ (片端ヒンジが発生している場合)
$⊿σ= 2・σ_y$ (ヒンジが発生していない場合)
$d$:部材有効せい(圧縮縁から引張鉄筋重心位置までの距離)(mm)
$\tau_{bu2} = a_2 \cdot a_1 \cdot \left( (0.085 \cdot b_{si2}+0.10) \cdot \sqrt{F_c}+k_{st2} \right)$
$τ_{bu2}$:2段目主筋の付着信頼強度(N/mm2)
$α_2$:2段目主筋に対する強度低減係数(=0.6)
$α_t$:梁の上端筋に対する付着強度低減係数
$0.75+F_c/400$ (梁の上端主筋の場合)
$01$ (上記以外の場合)
$b_{si2}$:2段目主筋の割裂長さ比
$b_{si2} = (b-N_2 \cdot d_{b2})/(N_2 \cdot d_{b2})$
$N_2$:2段目の主筋本数
$b_2$:2段目の主筋径(呼び名)(mm)
$k_{st2}$:2段目主筋に対する横補強筋効果
$k_{st2} = 99 \cdot (b_{si2}+1) \cdot p_w$
付着設計における2段目主筋は、断面最外縁から部材せい $D$の $1/4$の範囲に配筋された主筋で、1段目主筋以外の主筋と定義します。
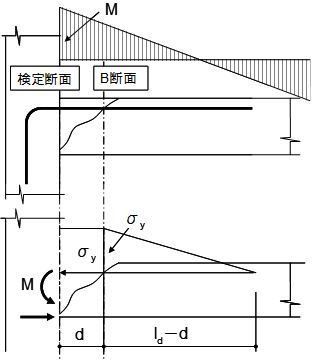
2段筋の必要付着長さ $L_d$は、RC規準による平均付着応力度の算定式を用いて求めます3)。下図に示すように、設計用付着応力度 $τ_f$は、検定断面の鉄筋の応力度 $σ_y$が検定断面から部材の有効せい $d$だけ離れた断面まで一定と見なし、B断面より一様な付着作用によって定着されるものと仮定します。よって、必要付着長さ $L_d$は検定断面を起点とする付着長さ $l_d$となります。
$L_d = \frac{\sigma_y \cdot a}{\tau_f \cdot \phi}+d$
$L_d$:必要付着長さ(mm)
$σ_y$:鉄筋の降伏強度(N/mm2)
$a$:鉄筋の断面積(mm2)
$τ_f$:設計用付着応力度(N/mm2)
$φ$:鉄筋の周長(mm)
3) 社)日本建築学会:鉄筋コンクリート構造計算規準・同解説;P.212-213,2010.2
c) 梁の靭性指針式による終局せん断信頼強度
「終局耐力条件」で「靭性保証型設計指針」を選択した場合、鉄筋コンクリート造梁の終局せん断信頼強度 $V_u$、付着破壊の影響を考慮したせん断信頼強度 $τ_{bu}$については、靭性指針4)により算定します。
また、設計用付着応力度 $τ_f$および2段目主筋の信頼強度 $τ_{bu2}$は、b)で前述した付着に対する設計と同様とします。
$V_u$:せん断信頼強度(N/mm2)
$V_u$= $min \left( V_{u1}, V_{u2}, V_{u3} \right)$
$V_{u1} = \mu p_{we}\sigma_{wy}b_ej_e+ \left( \nu \sigma_B- \frac{5p_{we}\sigma_{wy}}{\lambda} \right) \frac{bD}{2} \tan \theta$ (6.4.1)
$V_{u2} = \frac{\lambda \nu \sigma_B+p_{we}\sigma_{wy}}{3}b_ej_e$ (6.4.2)
$V_{u3} = \frac{\lambda \nu \sigma_B}{2}b_ej_e$ (6.4.3)
$μ$:トラス機構の角度を表す係数( $=2-20R_p$)
$R_p$:終局限界状態でのヒンジ領域の回転角(rad)
$p_w$:有効横補強筋比(%)( $=a_w/b_e$)
$a_w$:1組の横補強筋の断面積(mm2)
$s$:横補強筋の間隔(mm)
$σ_{wy}$:横補強筋の信頼強度(N/mm2)
$b_e$:トラス機構に関与する断面の有効幅(mm)
$j_e$:トラス機構に関与する断面の有効せい(mm)
$ν$:コンクリート圧縮強度の有効係数 $\left( =(1-20R_p)ν0 \right) $
$ν_0$:降伏ヒンジ・潜在ヒンジを計画しない時の有効係数 $\left( =0.7- \frac{σ_B}{200}\right)$
$σ_B$:コンクリートの圧縮強度(N/mm2)
$λ$:トラス機構の有効係数
$b$:梁幅(mm)
$D$:梁せい(mm)
$θ$:アーチ機構の圧縮束の角度
4) (社)日本建築学会:鉄筋コンクリート造建物の靭性保証型耐震設計指針・同解説;P.142-162,1997.7
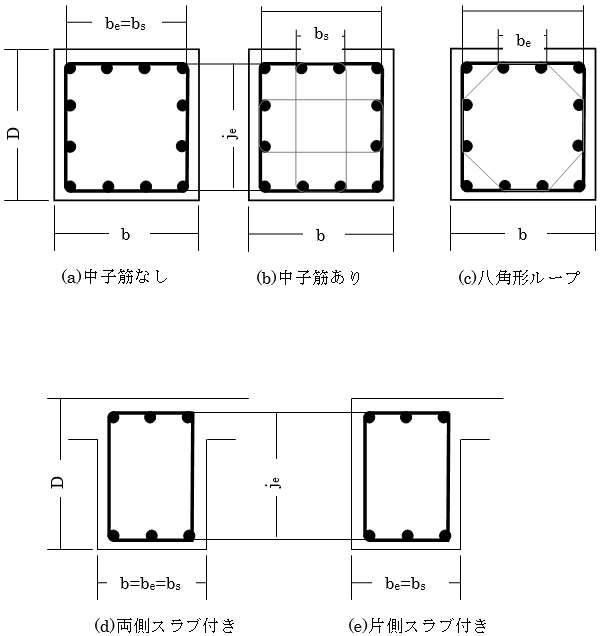
※ $b_e$は下記によります。
柱およびスラブ付きでない梁の場合は、図6.4.1(a)(b)(c)に示すように、外側の横補強筋のせん断力直交方向への芯々間隔とします。
両側スラブ付きの梁の場合は、図6.4.1(d)に示すように、 $b_e=b$とします。
片側スラブ付きの梁の場合は、図6.4.1(e)に示すように、スラブのない側の横補強筋からスラブのある側のコンクリート表面までを $b_e$とします。
※λは下記(6.4.8)によります。
$\lambda = 1- \frac{s}{2j_e}- \frac{b_s}{4j_e}$ (6.4.8)
ここで、bsは次式で算定します。
$b_s = \frac{b_e}{N_s+1}$ (6.4.9)
$N_s$:中子筋の本数(本)
※θは下記によります。
引張軸力を受ける柱では $tanθ=0$とします。
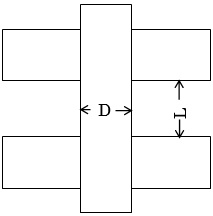
それ以外の柱・梁で、 $L/D \geqq 1.5$ の部材では、次式で算定します。
$\tan \theta =0.9 \times \frac{D}{2L}$ (6.4.10)
$L$:クリアスパン長さ(mm)(図6.4.2参照)
$L/D<1.5$の部材では次式で算定します。
$\tan \theta =\frac{\sqrt{L^2-D^2}-L}{D}$ (6.4.11)
$V_{bu}$: 付着破壊の影響を考慮したせん断信頼強度(N/mm2)
$Vb_u = min(V_{bu1}, V_{bu2} )$
$V_{bu1} = T_xj_e+ \left( \nu \sigma_B- \frac{2.5T_x}{\lambda b_e} \right) \frac{bD}{2} \tan \theta$ (6.8.14)
$V_{bu2} = \frac{\lambda \nu \sigma_B}{2}b_ej_e$ (6.8.15)
$T_x$:部材単位長さあたりに負担できる付着力
降伏ヒンジを計画しない部材: $T_x = \tau _{bu} \sum \phi _1+\tau _{bu2} \sum \phi_2$ (6.8.16a)
降伏ヒンジを計画する部材: $T_x = (1-10R_p)(\tau _{bu} \sum \phi_1+\tau _{bu2} \sum \phi_2)$ (6.8.16b)
$\sum \phi_1$:1段目主筋の周長の合計
$\sum \phi_2$:2段目主筋の周長の合計
$ν$:コンクリートの有効圧縮強度 係数終局せん断信頼強度によります