ブレース
ブレース
ブレースは、隣接する階の異なる2つの節点を端点として定義し、軸バネにモデル化します。ブレースに関する基本事項を以下に示します。
■ブレース断面は一様として断面性能および耐力を算定します。
■端部はピン接合とし、軸力のみを負担するものとします。ただし、「面内に拘束する」とした場合には面外方向には剛接合となります。
鉄骨ブレース
鉄骨造ブレースの軸非線形特性
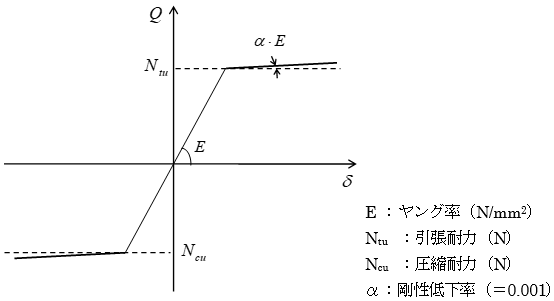
鉄骨造ブレースの軸非線形特性は、下図に示すバイリニアモデルで評価します。
引張耐力および圧縮耐力は指定により下記から選択可能です。
終局耐力(Nu)
$$N_u = \sigma_y \cdot A_n$$$σ_y$:降伏点強度(N/mm2)
$A_n$:全断面積(mm2)
許容応力度( $N_a$)
鉄骨ブレースの許容応力度は、鋼構造設計指針により次式で算定します2)。
引張
$$N_a = \sigma_{as} \cdot A_n$$$σ_{as}$:短期許容応力度(N/mm2)
$A_n$:全断面積(mm2)
圧縮
$$N_a = f_{cS} \cdot A_n$$
圧縮材の座屈の長期許容応力度( $fc_L$)は次式で算定します。なお、圧縮材の座屈の短期許容応力度( $fc_S$)は長期許容応力度( $fc_L$)の1.5倍とします。
$$ fc_L = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \frac{F}{\nu} \left( 1-0.4 \cdot \left( \frac{\lambda}{\Lambda} \right)^2 \right) & \displaystyle \left( \lambda \leq \Lambda \right) \\ \displaystyle \frac{\frac{18}{65} \cdot F}{ \left( \frac{\lambda}{\Lambda} \right)^2} & \displaystyle \left( \Lambda < \lambda \right) \end{array} \right. \end{align}$$
$fc_L$:圧縮材の座屈の長期許容応力度
$F$:鋼材の規準強度(N/mm2)
$λ$:有効細長比(= $l_k/i$)
$i$:座屈軸についての断面2次半径(mm)
$l_k$:有効座屈長さ(mm)
$Λ$:限界細長比
$ν$:安全率
$\Lambda = \frac{1500}{\sqrt{\frac{F}{1.5}}}$ $\nu = \frac{3}{2}+\frac{2}{3} \left( \frac{\lambda}{\Lambda} \right)^2$安定座屈耐力 $N_{sb}$
鉄骨ブレースの安定座屈耐力は次式で算定します。
$$ N_{sb} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \sigma_y \cdot A_n & \displaystyle \left( \lambda_B \leq 0.15 \right) \\ \displaystyle \frac{\sigma_y \cdot A_n}{11\lambda_B-0.65} & \displaystyle \left( 0.15 < \lambda_B \leq 0.3 \right)\\ \displaystyle \frac{\sigma_y \cdot A_n}{6\lambda_B-0.85} & \displaystyle \left( 0.35<\lambda_B \right) \end{array} \right. \end{align}$$$K_b$ : $0.75$
$\lambda_B = \frac{K_b \cdot L}{i} \cdot \sqrt{\frac{\sigma_y}{\pi^2E}}$
座屈拘束ブレース(直接入力)の軸非線形特性
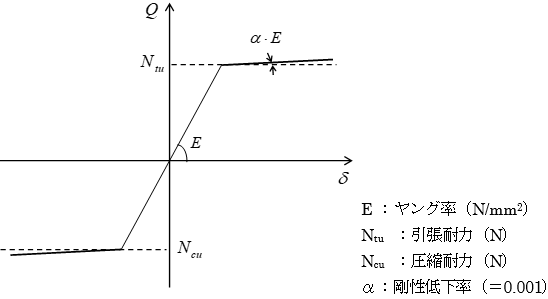
座屈拘束ブレース(直接入力)の軸非線形特性は、下図に示すバイリニアモデルで評価します。
座屈拘束ブレースの場合、引張および圧縮耐力は次式によります。
$$N_{y} = A_{n} \cdot \sigma_{y}$$メーカー製品ダンパーブレースの軸非線形特性
“制振要素"をご参照ください。
「制振要素」
1) 日本建築学会:鋼構造限界状態設計指針・同解説;P.20, 2010.2
2) 日本建築学会:鋼構造設計基準;1999.4