梁
梁
梁部材は、同一階の2つの節点を端点として定義し、両端に剛塑性回転バネを有する線材としてモデル化します。モデルの仮定条件は以下のとおりです。
■曲げ剛性、せん断剛性(弾性)、軸剛性(弾性)を持ち、指定によりねじれ剛性を考慮することが可能です。
■鉄筋コンクリート、鉄骨鉄筋コンクリート造梁の場合は、曲げひび割れを考慮します。
■梁の断面性能は中央の断面形状から算定します。鉄筋コンクリート造、鉄骨鉄筋コンクリート造梁の場合は、スラブを含めたコンクリート形状と鉄筋あるいは鉄骨の影響を考慮します。
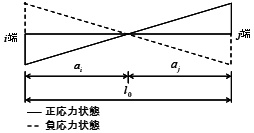
■梁の曲げ・せん断耐力は、端部の断面より求めます。曲げ耐力には、下図に示す部材の両端で計算した正負応力を採用し、せん断耐力は両端の正負応力状態について求めた絶対値の最小値を用います。
■せん断スパン( $M/Q$)およびモーメント反曲点長さ( $a$)は可撓長さ( $l_0$)の $1/2$とし、他端ピンの場合はせん断スパン( $M/Q$)が可撓長さ( $l_0$)に一致するものとします。
$a_i$, $a_j$:i端、j端のモーメント反曲点高さ( $ = 1/2 \cdot l_0 $)
$l_0$:内法スパン
共通
梁の曲げ非線形特性のモデル化
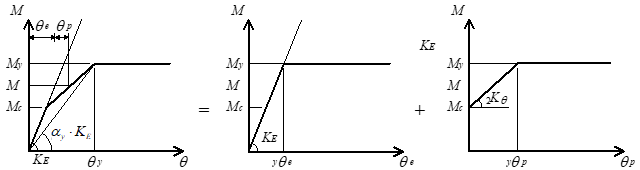
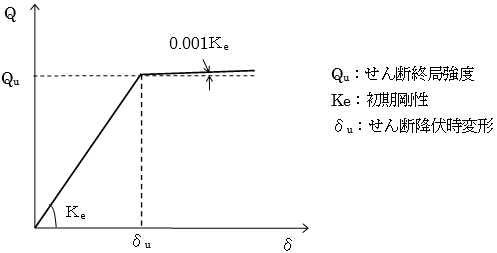
梁の曲げ非線形特性は、部材の両端に取付く剛塑性回転バネにより評価します。なお、塑性率の計算はバイリニアの場合は第1折れ点、トリリニアの場合は第2折れ点を起点とします。
部材の曲げ非線形特性( $M-θ$関係)は、曲げ降伏時剛性低下率( $α_y$)を用いて、トリリニア型のスケルトンカーブにモデル化します。
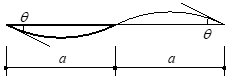
ここで、反曲点位置をaとしたとき、長さ2aとなるような逆対称モーメント分布を持つ仮想部材を考えます。
この部材の降伏変形角を $θ_y$とすると、せん断変形を考慮して下式で表されます。
$$\theta_y = \left( \frac{M_y \cdot a^2}{3 \cdot E \cdot I_e}+ \frac{M_y}{G \cdot A_s} \right) \cdot \frac{1}{a} \cdot \frac{1}{\alpha_y}$$この弾塑性の復元力特性から弾性変形分を差引いて、剛塑性回転バネの特性を求めます。降伏変形角(
$θ_y$)は、
曲げ降伏時変形角(yθe)と塑性変形角(yθp)の和により下式となります。
以上より、塑性変形(yθp)は下式となります。
$${_y}\theta_p = \left( \frac{1}{\alpha_y}-1 \right) \cdot \left( \frac{M_y \cdot a^2}{3 \cdot E \cdot I_e}+ \frac{M_y}{G \cdot A_s} \right) \cdot \frac{1}{a}$$したがって、曲げひび割れ後の材端回転バネのバネ定数( $_2 K_\theta$)は下式となります。
$$_2 K_\theta = \frac{M_y-M_c}{{_y}\theta_p}$$
$M_y$:曲げ降伏モーメント
$α_y$:曲げ降伏時剛性低下率
$a$:反曲点高さ
$E$:ヤング係数
$G$:せん断弾性係数
$I_e$:断面2次モーメント
$A_S$:せん断変形用断面積
鉄筋コンクリート造
鉄筋コンクリート造梁の曲げ復元力特性
鉄筋コンクリート造梁の曲げ復元力特性の諸元値を以下に示します。なお、耐震壁付梁の場合は弾性とします。
各耐力式に用いる主な記号は以下のとおりとします。
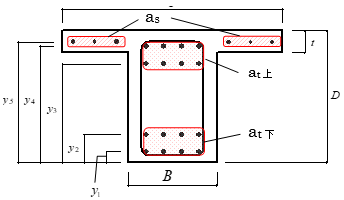
$y_i$ :梁下端からの各鉄筋重心までの距離
$a_i$:各鉄筋断面積
$i=1$ :下端1段筋
$i=2$ :下端2段筋
$i=3$ :上端1段筋
$i=4$:上端2段筋
$i=5$ :スラブ筋
$a_t$:引張鉄筋断面積
$a_s$:スラブ筋の断面積
$b$:T型梁の有効幅
$B$:梁幅
$D$:梁せい
$t$:スラブ厚
※ 鉄筋の剛性を考慮しない場合は、「剛性条件」→「RC造」で"各断面の剛性計算時,鉄筋の剛性を考慮しない"にチェックを入れる必要があります。
※ スラブ筋を考慮する場合は、「終局耐力条件」でスラブ筋の断面積を直接入力する必要があります。
※ スラブ筋の重心位置はスラブ厚(t)の1/2とします。
※ 初期設定では片持ち床のスラブ筋は考慮しません。考慮する場合は、「剛性計算条件」→「剛性条件1」で"協力幅の計算に片持ちスラブを含む"にチェックを入れる必要があります。
※ 片持ち床のスラブ筋を考慮した場合、曲げ終局強度を計算する際の圧縮縁から引張鉄筋重心までの距離はスラブ筋を考慮したうえで計算したものになります。
※ 引張鉄筋比( $p_t$)へのスラブ筋の考慮は以下のとおりとします。
■スラブ筋を考慮する場合
上端引張:
$p_t$ =
$(a_s + a_{t{上}})/(B \cdot D)$
下端引張:
$p_t$ =
$a_{t{下}}/(b \cdot D)$
■スラブ筋を考慮しない場合
上端引張:
$p_t$ =
$a_{t{上}}/(B \cdot D)$
下端引張:
$p_t$ =
$a_{t{下}}/(B \cdot D)$
・上端引張(スラブ引張)時は、梁幅Bと梁せいDからなる長方形梁を想定
・下端引張(スラブ圧縮)時は、T型梁の有効幅bと梁せいDからなる仮想の長方形梁を想定
※ 非線形解析においては、鉄筋およびコンクリートのヤング係数は下式によります1)。
$$E_c = 3.35 \cdot 10^4 \cdot \left( \frac{\gamma}{24} \right)^2 \cdot \left( \frac{F_c}{60} \right) ^\frac{1}{3}$$ $$E_s = 2.05 \cdot 10^5$$
$E_c$:コンクリートのヤング係数(N/mm2)
$γ$:コンクリートの気乾単位体積重量(kN/m3)
$F_c$:コンクリートの設計基準強度(N/mm2)
$E_s$:鉄筋のヤング係数(N/mm2)
1) 日本建築学会:鉄筋コンクリート構造計算基準・同解説;P.50-51,2010.2
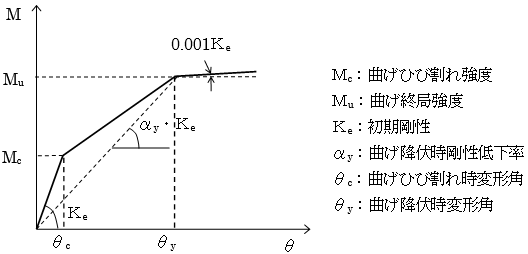
(1) 曲げひび割れ強度( $M_c$)
鉄筋コンクリート造梁の曲げひび割れ強度(Mc)は構造規定(略算式)により計算します2)。
$$M_c = \kappa \cdot \sqrt{F_c} \cdot Z_e$$$κ$:ひび割れモーメント算定用係数(=0.56)
$Z_e$:鉄筋を考慮した断面係数(mm3)
上端引張の場合 $I_e/(D-g)$
下端引張の場合 $I_e/g$
$I_e$:断面2次モーメント(mm4)
異種強度梁の場合、引張側のコンクリート強度(上端引張の場合 $F_{cu}$, 下端引張の場合 $F_{cd}$)を用います。
2) 国土交通省:2007年版建築物の構造関係技術基準解説書;P.621-623,2007.8
(2) 曲げ降伏時剛性低下率( $α_y$)
鉄筋コンクリート造梁の曲げ降伏時剛性低下率( $α_y$)は下式で算定します2)。
$$ \alpha_y = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle \left( 0.043+1.635 n \cdot p_t+0.043 \frac{a}{D} \right) \left( \frac{d}{D}\right)^2 & \displaystyle \left( 2.0 \leq \frac{a}{D} \leq 5.0\right) \\ \displaystyle \left(-0.0836+0.159 \frac{a}{D}\right) \left( \frac{d}{D}\right)^2 & \displaystyle \left( 1.0 \leq \frac{a}{D} < 2.0\right) \end{array} \right. \end{align}$$※ $ \frac{a}{D}<1.0$または $5.0 < \frac{a}{D}$の場合、 $\frac{a}{D}$はそれぞれ $1.0 , 5.0$とします。
$p_t$:引張鉄筋比(小数)
$a/D$:シアスパン比
$a$:せん断スパン(= $l_0/2$)(mm)
$l_0$:可撓長さ(mm)
$d$:有効せい(圧縮縁から引張鉄筋重心までの距離)(mm)
$n$:ヤング係数比(= $Es/Ec$)
・上端引張の場合
$p_t = \frac{\sum a_i}{B \cdot D} \quad d = \frac{\sum a_i \cdot y_i}{\sum a_i}$・下端引張の場合(指定によりb=Bとすることも可能です)
$p_t = \frac{\sum a_i}{b \cdot D} \quad d = \frac{\sum a_i \cdot (D-y_i)}{\sum a_i}$$a_i$:各鉄筋断面積(mm2)
$y_i$:梁下端からの各鉄筋重心位置(mm)
※ スラブ筋断面積が入力されている場合は、上端引張側の $p_t$にスラブ筋の断面積を含めて算定します。
※ T型梁または腰壁、垂壁付梁の場合は、求まった $α_y$を下式により補正します3)。指定により、補正しないこともできます。
・上端引張の場合
$α_y'=α_y \frac{I_{e0}+I_{wl}}{I_e+I_{wu}+I_{wl}}$※腰壁、垂壁が存在しない場合、 $α_y'=α_y \frac{I_{e0}}{I_e}$と等価
・下端引張の場合
$α_y'=α_y \frac{I_{e0}+I_{wl}}{I_e-I_{wu}+I_{wl}}$※腰壁、垂壁が存在しない場合、 $α_y'=α_y$と等価
$I_{e0}$:矩形断面の断面2次モーメント(mm4)
$I_e$:T型断面の断面2次モーメント(mm4)
$I_{wu}$:腰壁断面の断面2次モーメント(mm4)
$I_{wl}$:垂壁断面の断面2次モーメント(mm4)
異種強度梁の場合、ヤング係数比の算定において、引張側のコンクリート強度(上端引張の場合 $F_{cu}$, 下端引張の場合 $F_{cd}$)を用います。
3) 梅村魁;鉄筋コンクリート建物の動的耐震設計法;技報堂;P.106-108,1973.8
(3) 曲げ終局強度( $M_u$)
a) 大梁の曲げ終局強度
鉄筋コンクリート造梁の曲げ終局強度( $M_u$)は構造規定による略算式もしくはACI規準に基づく平面保持仮定により算定します4)。
略算式
$$M_u = 0.9 \cdot (\sum \sigma_{yi} \cdot a_i) \cdot d$$ $$ d = \frac{\sum \sigma_{yi} \cdot a_i \cdot d_i}{\sum \sigma_{yi} \cdot a_i} $$$σ_{yi}$:各引張鉄筋の降伏強度(N/mm2)
$a_i$:各引張鉄筋の断面積(mm2)
$d$:梁有効せい(圧縮縁から引張鉄筋重心位置までの距離)(mm)
$d_i$:圧縮縁から各引張鉄筋重心位置までの距離(mm)
4) 国土交通省:2007年版建築物の構造関係技術基準解説書;P.623,2007.8
平面保持
「鉄筋コンクリート造柱の終局耐力」をご確認ください。
b) 腰(垂)壁付き大梁の曲げ終局強度
腰(垂)壁付き鉄筋コンクリート造梁の曲げ終局強度( $M_u$)は構造規定により算定します4)。
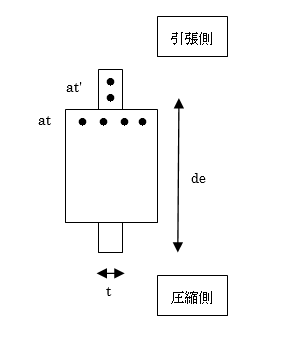
$$M_u=a_{te} \cdot σ_y \cdot (d_e-0.5x_n)$$ただし、 $a_{te}=a_t+Σa_{t'}\left(\frac{σ_{y'}}{σ_y}\right)$ かつ $a_{te}\le(0.85F_c \cdot t \cdot x_{nb}/σ_y)-Σa_{t'}\left(\frac{σ_{}y'}{σ_y}\right)$
$x_n=a_{te} \cdot σ_{y}/(0.85F_c \cdot t)$
$F_c$:コンクリート圧縮強度
$t$:圧縮側の壁厚(壁がない場合、 $t=b$)
$_cε_B$:コンクリートの圧縮強度歪み( $0.002$)
$_sε_y$:梁主筋降伏点時の歪み( $σ_y/_sE$)
c) 異種強度梁の曲げ終局強度
略算式
異種強度梁特有の変更はありません。
平面保持
終局曲げ耐力の算定における留意点は以下となります。
- $F_c$を圧縮側のコンクリート強度(上端引張の場合 $F_{cd}$, 下端引張の場合 $F_{cu}$)と置き換えて既存の式で算定します。
- 計算条件>部材復元力特性計算条件>終局耐力条件2>平面保持スラブの設定の片側スラブ幅の値を採用します。
- 中立軸位置と水平接合面位置が異なる場合でも、中立軸位置より上は $F_{cu}$, 中立軸位置より下は $F_{cu}$とします(下図参照)。
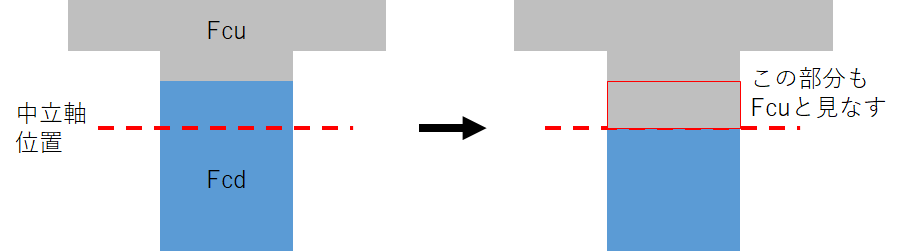
平面保持を選択した場合の終局曲げ耐力の算定における留意点
鉄筋コンクリート造梁のせん断復元力特性
せん断復元力特性は指定により考慮できます。鉄筋コンクリート造梁のせん断復元力特性の諸元値を以下に示します。なお、壁付梁の場合は指定によらず弾性とします。
せん断終局耐力は上端引張、下端引張の耐力の平均値を採用します。
(1) 大梁のせん断終局強度(RC)
RC大梁のせん断終局強度は下記に式により計算されます。スラブについては $b_e≦1.2b$ の範囲で考慮されます。
$$Q_{su} = \left( \frac{k \cdot p_t^{0.23} (18+F_c)}{ \displaystyle \frac{M}{(Q \cdot d)}+0.12}+0.85 \sqrt{p_w \cdot \sigma_{wy}} \right) \cdot b_e \cdot j_e$$ $\kappa : 0.053 または 0.068$$p_{te}$ : $a_t/(b・d)$
$d$ : 大梁の引張鉄筋の中心から圧縮縁までの距離
$p_w・σ_wy$ : 大梁の帯筋比とその降伏強度の積
$σ_0$ : $N/(b・j)$
$j : 7d/8$$M/Q・d$ : せん断スパン比 ( $1.0≦M/Q・d≦3.0$)
| $κ$ | $σ_{wy}$ | |
|---|---|---|
| ウルボン1275 | $0.053$ | 特になし |
| パワーリング785 | $0.053$ | $σ_{wy}=25・Fc (Fc<32)$ |
| パワーリング685 | $0.068$ | 特になし |
| エムケーフープ | $0.053$ | $σ_{wy}=25・Fc (Fc < 31.4)$ |
(2) 腰(垂)壁付き大梁のせん断終局強度(RC)
腰(垂)壁付きRC大梁のせん断終局強度は下記に式により計算されます。
$$Q_{su} = \left( \frac{k \cdot p_t^{0.23} (18+F_c)}{\displaystyle \frac{M}{(Q \cdot d)}+0.12}+0.85 \sqrt{p_we \cdot \sigma_{wy}} \right) \cdot b_e \cdot j_e$$$k$: $0.053$ または $0.068$
$p_{te}:a_{t}/(b_{e} \cdot d_{e})$$d_{e}$ : 大梁の引張鉄筋の中心から圧縮側壁の最外縁までの距離
$p_{we} \cdot \sigma_{wy}$ : $p_w \cdot \sigma_{wy}(b/b_e)+p{_sh} \cdot \sigma_{sy}(t/b_e)$
$p_{w} \cdot \sigma_{wy}$ : 大梁の帯筋比とその降伏強度の積
$p_{sh} \cdot \sigma_{sy}$ : 腰(垂)壁の横筋比とその降伏強度の積
$\sigma_{0e}$ : $N/(b_e \cdot j_e)$
$j_{e}$ : $7d_{e}/8$
$b_{e} = \Sigma A/L'$ : 断面積とせいを同じにしたときの等価幅
$M/Q \cdot d_{e} = \frac{h_{CW0}}{L'} \quad (0.5 \leq M/Q \cdot d \leq 2.0)$$h_{CW0}$:反曲点の高さ
$L'$:腰(垂)壁を含む全せい
高強度せん断補強筋を用いた場合は以下が適用されます。
| $κ$ | $σ_{wy}$ | |
|---|---|---|
| ウルボン1275 | $0.053$ | 特になし |
| パワーリング785 | $0.053$ | $σ_{wy}=25・Fc (Fc<32)$: |
| パワーリング685 | $0.068$ | 特になし |
| エムケーフープ | $0.053$ | $σ_{wy}=25・Fc (Fc< 31.4)$ |
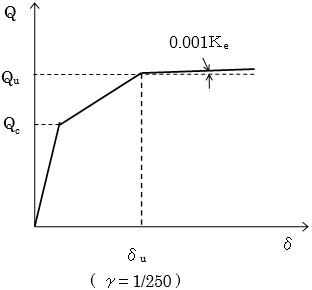
(3) 大梁のせん断ひび割れ強度(RC)
指定により、ひび割れを考慮したトリリニアとしてモデル化します。ひび割れ耐力は以下のように計算します。せん断降伏時歪みは1/250としてトリリニアモデルを作成します。
$$Q_c = \left( \frac{0.061 \cdot (Fc+49)}{\left( \frac{M}{Q \cdot d} \right)+1.7} \right) \cdot b \cdot j$$
鉄筋コンクリート造梁の軸復元力特性
指定により、軸復元力特性を考慮する場合には以下の式により復元力特性を設定します。
(1) 引張ひび割れ軸力
$$N_{ct} = \kappa \sqrt{F_c} \cdot A_c$$$κ$:ひび割れ軸力算定用係数(=0.56)
$Ac$:コンクリート断面積(mm2)
$Fc$:コンクリート強度(N/ mm2)
(2) 引張降伏軸力
$$N_{ut} = at \cdot \sigma_y$$$a_t$:鉄筋断面積(mm2)
$σ_y$:鉄筋材料強度(N/mm2)
(3) 圧縮降伏軸力
$$N_{uc} = at \cdot \sigma_y+F_c \cdot (A_c-at)$$鉄骨造
鉄骨梁の曲げ復元力特性
指定により、曲げ復元力特性を考慮する場合には以下の式により復元力特性を設定します。
(1) 全塑性モーメント $M_p$
$$M_p=Z_p・σ_y$$$Z_p$:塑性断面係数(mm3)
$σ_y$:鉄骨降伏強度(N/mm2)
(2) 横座屈モーメント $M_{cr}$
横座屈を考慮する場合、鋼構造塑性設計指針に基づき以下の式により計算します。鉄骨材料はフランジ部の材料を採用し、横座屈を考慮する断面形状はH形鋼のみとします。
a) SN400, SS400,SM400材( $σ_y$=235N/mm2)
$$ \frac{M_{cγ}}{M_P} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle 1.0 & \left( 0 \leq \frac{l_b・H}{A_f} \leq 300 \right) \\ \displaystyle 1-0.00075 \cdot \left( \tfrac{l_b・H }{A_f}-300\right) & \left( 300 < \frac{l_b・H}{A_f} \leq 835 \right)\\ \displaystyle \frac{500}{\frac{l_b \cdot H}{A_f}} & \left( 835 < \frac{l_b・H}{A_f} \right) \end{array} \right. \end{align}$$b) SN490, SM490, SM490T材( $σ_y$=325N/mm2)
$$ \frac{M_{cγ}}{M_P} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle 1.0 & \left( 0 \leq \frac{l_b・H}{A_f} \leq 220 \right) \\ \displaystyle 1-0.0010 \cdot \left( \tfrac{l_b・H }{A_f}-220 \right) & \left( 220 < \frac{l_b・H}{A_f} \leq 605 \right)\\ \displaystyle \frac{363}{\frac{l_b \cdot H}{A_f}} & \left( 605 < \frac{l_b・H}{A_f} \right) \end{array} \right. \end{align}$$c) その他
$$ \frac{M_{cγ}}{M_P} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle 1.0 & \left( 0 \leq \frac{l_b・H}{A_f} \leq \frac{70500}{α} \right) \\ \displaystyle 1- \frac{0.4}{ \frac{117000}{0.6σ_y} - \frac{70500}{σ_y}} \cdot \left( \tfrac{l_b・H}{A_f}- \tfrac{70500}{σ_y} \right) & \left( \frac{70500}{α} < \frac{l_b・H}{A_f} \leq \frac{117000}{0.6σ_y} \right)\\ \displaystyle \frac{ \frac{117000}{σ_y}}{{l_b}{A_f}} & \left( \frac{117000}{0.6σ_y} < \frac{l_b・H}{A_f} \right) \end{array} \right. \end{align}$$$l_b$:横方向補剛材の間隔(mm)
$H$:梁のせい(mm)
$A_f$:圧縮フランジの断面積(mm2)
鉄骨梁の軸復元力特性
指定により、軸復元力特性を考慮する場合には以下の式により復元力特性を設定します。
(1) 引張降伏軸力・圧縮降伏軸力
$$N_u = A_f \cdot \sigma_{fy}+A_w \cdot \sigma_{wy}$$$A_f$:フランジ断面積(mm2)
$A_w$:ウェブ断面積(mm2)
$σ_{fy}$:鉄筋材料強度(N/mm2)
$σ_{wy}$:鉄骨材料強度(N/mm2)
鉄骨鉄筋コンクリート造
鉄骨鉄筋コンクリート造梁の曲げ復元力特性
鉄骨鉄筋コンクリート造梁の曲げ復元力特性は、RC部分をトリリニア、S部分をバイリニアとして累加し、エネルギー吸収能力において等価なトリリニア型スケルトンカーブを求めます。
鉄骨鉄筋コンクリート造梁のせん断復元力特性
(1) 大梁のせん断終局強度(SRC)
SRC大梁のせん断終局強度は下記の3式からの選択により計算されます。
a) SRC規準
$$Q_u = ({_r}Q_u+{_s}Q_u)$$ $$_rQ_u= min(_rQ_{u1}, _rQ_{u2})$$ $$_sQ_u= min(_sQ_{u1},_sQ_{u2})$$ $$_rQ_{u1}=b \cdot {_r}j(0.5 \times \alpha \cdot f_s+0.5 \cdot {_r}p_w \cdot _{rw}\sigma_y)$$ $$_rQ_{u2}=b \cdot {_r}j(b'/bf_s+{_r}p_w \cdot _{rw}\sigma_y)$$ $$_{s}Q_{u1}={_s}A_w \cdot {_s}\sigma_y/ \sqrt{3}$$ $$_{s}Q_{u2}=\Sigma{_s}M_u/l'$$ $$f_s = \min (0.15 \times Fc,22.5+ \frac{4.5 \times Fc}{100})$$ $$ a = 4/ (M/(Q \cdot rd)+1 ) かつ 1 \leq a \leq 2 $$$b$:梁幅
$b'$:鉄筋フランジ位置のコンクリート有効幅
$_rj$:鉄筋コンクリート部分の応力中心間距離
$_rd$:梁の有効せい
$_rp_w$:せん断補強筋比
$_{rw}\sigma_y$:せん断補強筋の材料強度
$_sA_w$:せん断力が作用する方向の鉄骨ウェブ断面積
$_s\sigma_y$:鉄骨ウェブの材料強度
$F_c$:コンクリートの設計基準強度
$_sM_u$:鉄骨部分の一端あるいは他端における全塑性モーメント
$l'$:内法スパン
b) SRC診断式
スラブについては $b_e≦1.2b$の範囲で考慮されています。
$$Q_{su} = \left( \frac{k \cdot p_t^{0.23} \cdot k_{cs}(18+F_c)}{M/(Q \cdot d)+0.12}+0.85 \sqrt{p_w \cdot \sigma_{wy}} \right) \cdot b_e \cdot j_e+{_s}Q_u$$ $$ _sQ_u = min \displaystyle \left( \frac{2 \cdot _sM_0}{h_0} , t_w \cdot h_w \cdot _s \sigma_{wy} \sqrt{3} \right)$$$k$: $0.053$または $0.068$
$p_{w}:a_{t}/(b \cdot d)$$k_{cs}:(0.5+b`/b)$かつ1.0以下
$d$:大梁の引張鉄筋の中心から圧縮縁までの距離
$p_{w} \cdot \sigma_{wy}$:大梁の帯筋比とその降伏強度の積
$\sigma_{0}:N/(b \cdot j)$$j$: $7d/8$
$M/Q \cdot d$:せん断スパン比 $(1.0≤M/Q \cdot d≤3.0)$
c) 構造関係技術基準解説書
$$Q_u = (_{r}Q_u+{_s}Q_u)$$ $$_rQ_u= min(_rQ_{u1}, _rQ_{u2})$$ $$_sQ_u=min(_sQ_{u1}, _sQ_{u2})$$ $$_rQ_{u1}=b \cdot _rj ( \alpha \cdot f_s+0.5 \cdot_rp_w \cdot _{rw} \sigma_y)$$ $$_rQ_{u2}= b \cdot _rj ( 2b'/bf_s+_rp_w \cdot _{rw} \sigma_y)$$ $$_sQ_{u1} = _sA_w \cdot _s\sigma _y/\sqrt{3}$$ $$_sQ_{u2} = \Sigma _sM_u/l'$$ $$f_s = \min ( Fc/20,(5+Fc/100) \cdot 1.5 )$$ $$α = 4/ (M/(Q \cdot rd)+1 )$$
$b$:梁幅
$b'$:鉄骨フランジ位置のコンクリート有効幅
$_{r}j$:鉄骨コンクリート部分の応力中心間距離
$_{r}d$:梁の有効せい
$_rP_w$:せん断補強筋比
$_{rw}\sigma_y$:せん断補強筋の材料強度
$_rA_w$:せん断力が作用する方向の鉄骨ウェブ断面積
$_s\sigma_y$:鉄骨ウェブの材料強度
$F_{c}$:コンクリートの設計基準強度
$_sM_u$:鉄骨部分の一端あるいは他端における全塑性モーメント
$l'$:内法スパン
(2) 大梁のせん断終局強度(非充腹SRC)
a) 格子材
非充腹SRC(格子材)のせん断耐力式は以下によります。
$$Q_{su} = \left( \frac{k \cdot p_t^{0.23} \cdot k_{cs}(18+F_c)}{M/(Q \cdot d)+0.12}+0.85 \sqrt{{_r}p_w \cdot {_r}\sigma_{wy}+ \frac{1}{2}{_s}p_w \cdot {_s}\sigma_{wy}} \right) \cdot b_e \cdot j$$$κ$: $0.053$または $0.068$
$b$:梁の断面幅
$be$:梁の有効幅で以下の式による
$be=ΣAg/D$$Ag$:スラブの断面積を加算した梁の全断面積
$d$:梁の有効せい
$j$:応力中心間距離( $=0.8D$)
$p_t$:引張鋼材比( $_rp_t+_sp_t$)(%)
$_rp_t$:引張鉄筋比(%)
$_sp_t$:引張鉄骨比(%)
$_rp_w$:せん断補強筋比(= ${_r}a_w/(b\cdot {_r}s)$)
$_sp_w$:帯板比(= $_sa_w/(b・_ss)$)
$_ra_w$:1組のせん断補強筋断面積
$_sa_w$:1組の帯板の断面積
$_rs$, $_ss$:それぞれせん断補強筋および帯板の間隔
$_rσ_{wy}$, $_sσ_{wy}$:それぞれせん断補強筋および帯板の降伏点強度
$M/Q$:せん断スパン、弾性水平荷重解析結果より計算
$M/Q・d$:せん断スパン比( $1.0≦M/Q・d ≦3.0$)
b) ラチス材
非充腹SRC(ラチス材)のせん断耐力式は以下によります。
$$Q_{su} = \left( \frac{k \cdot {_r}p_t^{0.23} \cdot k_{cs}(18+F_c)}{M/(Q \cdot d)+0.12}+0.85 \sqrt{{_r}p_w \cdot {_r}\sigma_{wy}} \right) \cdot b_e \cdot {_r}j+{_s}Q_u$$ $${_s}Q_u=min\left(\frac{2\cdot{_s}M_0}{h_0}, {_D}A_s\cdot \sigma _y \cdot sin\theta\right) $$
$κ$ : $0.053$または $0.068$
$b$ :梁の断面幅
$be$ :梁の有効幅で以下の式による
$be=ΣAg/D$$Ag$ :スラブの断面積を加算した梁の全断面積
$d$ :梁の有効せい
$j$ :応力中心間距離( $=0.8D$)
$p_t$ :引張鋼材比( $_rp_t+_sp_t$)(%)
$_rp_t$ :引張鉄筋比(%)
$_sp_t$ :引張鉄骨比(%)
$_rp_w$ :せん断補強筋比(= $_ra_w/(b・_rs$))
$_sp_w$ :帯板比(= $_sa_w/(b・_ss$))
$_ra_w$ :1組のせん断補強筋断面積
$_sa_w$ :1組の帯板の断面積
$_rs$, $_ss$ :それぞれせん断補強筋および帯板の間隔
$ _rσ _{wy} $ , $ _sσ _{wy} $ :それぞれせん断補強筋および帯板の降伏点強度
$M/Q$ :せん断スパン、弾性水平荷重解析結果より計算
$M/Q・d$ :せん断スパン比( $1.0≦M/Q・d ≦3.0$)
$h_o$ :内法長さ
${_D}A$ :ラチス材の断面積
$θ$ :ラチス材と材軸のなす角
(3) 腰(垂)壁付き大梁のせん断終局強度(SRC)
腰(垂)壁付きSRC大梁のせん断終局強度は下記に式により計算されます。
$$Q_{su} = \left( \frac{k \cdot p_t^{0.23} \cdot k_{cs}(18+F_c)}{M/(Q \cdot d)+0.12}+0.85 \sqrt{p_{we} \cdot \sigma_{wy}} \right) \cdot b_e \cdot j_e$$
$k$ :
$0.053$または
$0.068$
$k_cs$ :梁材の鉄骨フランジ側面のせん断破壊による低減係数
$0.5+b'/b$ で1以下の値
$p_{te}$ :
$a_t/(b_e\cdot d_e)$
$d_e$ :大梁の引張鉄筋の中心から圧縮側壁の最外縁までの距離
$p_{we}\cdot \sigma_{wy}$ :
$p_w\cdot \sigma_{wy}(b/b_e)+p_{sh}\cdot\sigma_{sy}(t/b_e)$
$p_w\cdot \sigma_{wy}$ :大梁の帯筋比とその降伏強度の積
$p_sh{sh}\cdot \sigma_{sy}$ :腰(垂)壁の横筋比とその降伏強度の積
$p_{te}$ :
$N/(b_e\cdot j_e)$
$p_{te}$ :
$7d_e/8$
$b_e=\Sigma A/L'$
$M/Q\cdot d_e = \frac{h_{cw0}}{L'}$
$h_{cw0}$ : 半曲点高さ
$L'$ : 腰(垂)壁を含む全せい

鉄骨鉄筋コンクリート造梁の軸復元力特性
指定により、軸復元力特性を考慮する場合には以下の式により復元力特性を設定します。
(1) 引張ひび割れ軸力
$$N_{ct} = \kappa \sqrt{F_c} \cdot A_c$$$κ$:ひび割れ軸力算定用係数(=0.56)
$Ac$:コンクリート断面積(mm2)
$Fc$:コンクリート強度(N/ mm2)
(2) 引張降伏軸力
$$N_{ut} = at \cdot \sigma_{yr}+A_{st} \cdot \sigma_{ys}$$$at$:鉄筋断面積(mm2)
$σ_{yr}$:鉄筋材料強度(N/mm2)
$σ_{ys}$:鉄骨材料強度(N/mm2)