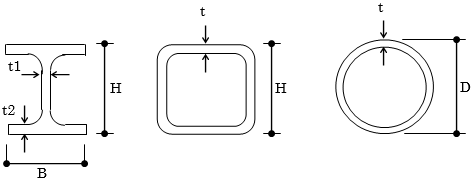
鉄骨造柱の断面検定
記号説明
$A$ :全断面積
$A_w$ :ウェブ有効断面積
$Z$ :断面係数
$f_t$ :許容引張応力度
$f_b$ :許容曲げ応力度
$f_s$ :許容せん断応力度
$f_c$ :許容圧縮応力度
$σ_b$ :曲げ応力度
$σ_c$ :圧縮応力度
$τ$ :せん断応力度
$N$ :設計用軸力
$M$ :設計用曲げモーメント
$Q$ :設計用せん断力
軸力と曲げモーメントに対する検討
a) H形鋼
$σ_c=N/A$ :圧縮応力度
$σ_{bX}=M_X/Z_y$ :曲げ応力度
$σ_{bY}=M_Y/Z_x$$τ=Q/(t_1・H)≦f_s$ :せん断応力度
$σ_c/f _c+σ _{bX}/f _b+σ _{bY}/f _b≦1.0$強軸まわりは、必ず横座屈( $l_b$)を考慮したfb、弱軸まわりは $f_b=f_t$
$l_b$は階高とします
b) 角形鋼管
$σ_c=N/A$ $σ_{bX}=M_X/Z_y$ $σ_{bY}=M_Y/Z_x$ $τ=2Q/A$ $σ_c/f_c+σ_{bX}/f_b+σ_{bY}/f_b≦1.0$$f_b=f_t$とします。
c) 鋼管
$σ_c=N/A$ $cσ_b = (M_{X}^2 + M_{Y}^2)^{1/2} /Z_c$$tσ_b $ = $(M_{X}^2 + M_{Y}^2)^{1/2} /Z_t$
$τ=2(Q_{X^2}+Q_{Y^2})^{1/2}/A$ $σ_c/f_c+σ_b/f_b≦1.0$せん断に対する検討
$\frac{\sqrt{\sigma^2+3\tau^2}}{f_t} \leq 1$ …(1)
$\frac{\tau}{f_s} \leq 1$ …(2)
a) H形断面の場合
・曲げ許容応力度にウェブを考慮する場合
検定値は(1)または(2)の大きい方とします。
その際、 $σ=σ_c+σ_{b'}、σ_{b'}=σ_{b×}(H -- 2・t2) / H$とします。
・曲げ許容応力度にウェブを考慮しない場合
検定値は(2)とします。
b) それ以外の断面の場合
検定値は(1)または(2)の大きい方とします。
その際、 $σ=σ_c+σ_{bx}+σ_{by}$とします。
柱の座屈長さ係数は、「鋼構造塑性設計指針」(6.65)~(6.67)式により、水平移動が拘束されない場合の座屈長さ係数Kを求めます。
座屈長さ係数は、以下の式より求めます。
$\frac{G_AG_B(\pi /K)^2-36}{6(G_A+G_B)} = \frac{\pi /K}{\tan (\pi /K)}$G:節点に集まる柱と梁の剛度の比
$G = \frac{\sum (l_c/l_c)}{\sum (l_g/l_g)}$添え字のA,Bは、柱の両端の節点を示します。
柱端がピン接合の場合は、G=10とします。
節点に接する梁が無い場合は、G=10とします。
混合構造の場合、節点に接する部材の構造種別がRC造またはSRC造のときは、その部材の剛性をヤング係数比により補正して計算します。
節点に接する部材の角度は考慮していません。
一本部材の指定は考慮していません。
梁の結合状態および支点の状態は考慮していません。
$I$:断面2次モーメント 添え字cは柱、gは梁
$l$:部材の長さ 添え字cは柱、gは梁
特殊形状による材長を考慮します。
$∑$:節点に集まる部材についての和
幅厚比の検討
a) 部材ランクの検討 ※部材ランク検討機能は現状では一部対応となります。
構造規定の幅厚比により、部材ランクを検討します。
| 部材 | 断面 | 部位 | 鋼種 | FA | FB | FC | FD |
|---|---|---|---|---|---|---|---|
| 柱 | H型鋼 | フランジ | 400N/mm2級 490N/mm2級 | 9.5 8 | 12 10 | 15.5 13.2 | 左記以外 |
| ウェブ | 400N/mm2級 490N/mm2級 | 43 37 | 45 39 | 48 41 | |||
| 円形鋼管 | - | 400N/mm2級 490N/mm2級 | 50 36 | 70 50 | 100 73 | ||
| 角形鋼管 | - | STKR400 | 33 | 37 | 48 | ||
| - | STKE490 | 27 | 32 | 41 | |||
| - | BCR295 | 30 | 34 | 43 | |||
| - | BCP235 | 33 | 37 | 48 | |||
| - | BCP325 | 27 | 32 | 41 | |||
| 梁 | H型鋼 | フランジ | 400N/mm2級 490N/mm2級 | 9 7.5 | 11 9.5 | 15.5 13.2 | |
| ウェブ | 400N/mm2級 490N/mm2級 | 60 51 | 65 55 | 71 61 |
幅厚比の検討式、およびb、dの取り方を以下に示します。
| 断面 | 部位 | 検討式 | |
|---|---|---|---|
| H形鋼 | フランジ | $\frac{b}{t_2}$ | $b=\frac{B}{2}$ |
| ウェブ | $\frac{d}{t_1}$ | $d=H-2t_2$ | |
| 角形鋼管 | - | $\frac{d}{t}$ | $d=H$ |
| 鋼管 | - | $\frac{d}{t}$ | $d=D$ |