鉄骨造梁の断面検定
記号説明
$A$ :全断面積
$A_w$ :ウェブ有効断面積
$Z$ :断面係数
$f_t$ :許容引張応力度
$f_b$ :許容曲げ応力度
$f_s$ :許容せん断応力度
$f_c$ :許容圧縮応力度
$σ_b$ :曲げ応力度
$σ_c$ :圧縮応力度
$τ$ :せん断応力度
$N$ :設計用軸力
$M$ :設計用曲げモーメント
$Q$ :設計用せん断力
曲げモーメント、せん断に対する検討
a) H形鋼全断面
端部
$σ_b=M/Z$ $τ=Q/(t_1・H)$$σ_b/f_b≦1.0$ :曲げ応力度比
$\frac{\sqrt{\sigma_b'^2+3\tau^2}}{f_t} \leq 1$ :せん断検定比(1) ここで、 $σ_{b'}=σ_{b×}(H - 2・t_2) / H$
$\frac{\tau}{f_s} \leq 1$ :せん断検定比(2)
max((1)式、(2)式) :せん断検定比
※指定により(2)のみとすることが可能です。
※許容曲げモーメント算定時にウェブを考慮しない場合には(2)で検定します。
中央
$σ_b=M/Z$$σ_b/f_b≦1.0$ (長期)
$\frac{\sqrt{\sigma_b'^2+3\tau^2}}{f_t} \leq 1$ :せん断検定比(1) ここで、 $σ_{b'}=σ_{b×}(H - 2・t_2) / H$
$\frac{\tau}{f_s} \leq 1$ :せん断検定比(2)
max((1)式、(2)式) :せん断検定比
※指定により(2)のみとすることが可能です。
※許容曲げモーメント算定時にウェブを考慮しない場合には(2)で検定します。
b) H形鋼(ウェブ非考慮)
曲げモーメント ・・・フランジ負担
せん断 ・・・ウェブ負担
端部
$σ_b=M/(h・B・t_2)$ $τ=Q/(t_1・H')$ $σ_b/f_b≦1.0$$\frac{\tau}{f_s} \leq 1$ :せん断検定比
中央
端部に同じ
c) 大梁必要横補剛数の算定
$n=(170-λ_y)/20$ (SS400級)
$n=(130-λ_y)/20$ (SM490級)
ただし、 $λ_y=L/i_y$ (梁の弱軸に関する細長比)
$i_y=√(l_y/A)$ (梁の弱軸に関する回転半径)
d) たわみ量の検定
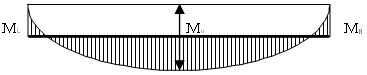
梁中央部のたわみを次の仮定にしたがって計算します。
中央断面が部材全長にあると仮定します。
応力状態は元の荷重パターンに拘わらず等分布荷重を想定し、下図のようであると仮定します。中央のたわみSは下式により求めます。
e) 横座屈長さLbの計算方法
フランジの拘束条件を「横補剛材による拘束」としている場合、以下のように横座屈長さを計算します。
(1) 横座屈長さを直接入力した場合
- 始端:「始端横座屈長(mm)」の値
- 始端側ジョイント位置:「中央座屈長(mm)」の値
- 中央:「中央座屈長(mm)」の値
- 終端側ジョイント位置:「中央座屈長(mm)」の値
- 終端:「終端横座屈長(mm)」の値
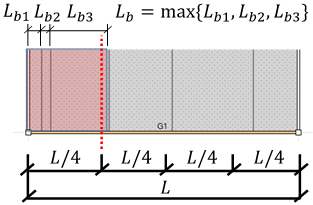
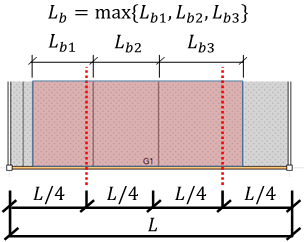
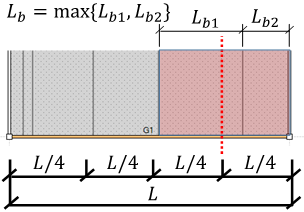
(2) 横座屈長さ自動計算の場合(直接入力していない場合)
- 始端:始端からL/4位置までの横補剛間隔の内、最大のもの
- 始端側ジョイント位置:始端からL/4位置の横補剛間隔
- 中央:部材中心から両端にL/4位置までの補剛間隔の内、最大のもの
- 終端側ジョイント位置:始端から3L/4位置の横補剛間隔
- 終端:3L/4位置から終端までの横補剛間隔の内、最大のもの
始端の横座屈長さ計算の例
中央の横座屈長さ計算の例
終端の横座屈長さ計算の例