鉄筋コンクリート造梁の断面検定
記号説明
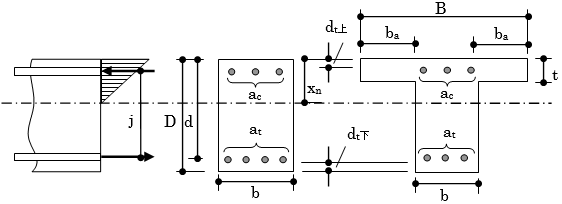
$B$ :T形断面部材の有効幅(mm)
$b$ :長方形梁の幅(mm)
$D$ :梁せい(mm)
$d_t$ :引張縁から引張鉄筋重心までの距離(mm)
$d$ :圧縮縁から引張鉄筋重心までの距離(有効せい)(=D-dt)(mm)
$j$ :梁の応力中心間距離(=7/8・d)(mm)
$a_t$ :引張鉄筋の断面積(mm2)
$a_c$ :圧縮鉄筋の断面積(mm2)
$p_w$ :せん断補強筋比(%)
$α_L$ :長期のせん断スパン比M/(Qd)による割増係数
$α_{S1}$ :短期正加力時のせん断スパン比M/( $Q_d$)による割増係数
$α_{S2}$ :短期負加力時のせん断スパン比M/( $Q_d$)による割増係数
$l$ :梁の内法スパン長さ(mm)
$t$ :スラブ厚(mm)
[梁の曲げに対する断面算定]
$M_L$ :長期曲げモーメント
$M_{sn}$ :積雪荷重曲げモーメント
$M_{E1}$ :正加力時の地震荷重による曲げモーメント
$M_{E2}$ :負加力時の地震荷重による曲げモーメント
$M_{w1}$ :正加力時の風圧力による曲げモーメント
$M_{w2}$ :負加力時の風圧力による曲げモーメント
$M_S$ :短期設計用曲げモーメント注1)
$M_{AL}$ :長期許容曲げモーメント
$M_{AS}$ :短期許容曲げモーメント
$M_y$ :終局曲げ強度
$M_L/M_{AL}$ :長期曲げモーメントに対する検定値
$M_S/M_{AS}$ :短期曲げモーメントに対する検定値
[梁のせん断に対する断面算定]
$Q_L$ :長期せん断力
$Q_{sn}$ :積雪荷重によるせん断力
$Q_E$ :地震荷重によるせん断力
$Q_w$ :風圧力によるせん断力
$Q_D$ :短期設計用せん断力
$Q_{AL}$ :長期許容せん断力
$Q_{AS}$ :短期許容せん断力
$Q_L/Q_{AL}$ :長期せん断力に対する検定値
$Q_D/Q_{AS}$ :短期せん断力に対する検定値
曲げモーメントに対する検討
梁の長期および短期の許容曲げモーメントが設計用曲げモーメント以上であることを以下の検定式により確認します。
$ M_L/M_{AL} \verb|≦|1.0 $ 長期曲げモーメントに対する検定
$ M_S/M_{AS} \verb|≦|1.0 $ 短期曲げモーメントに対する検定
スラブ付き梁であるT形梁の有効幅(B)は、長方形梁の幅(b)に両側または片側の協力幅( $b_a$)を加えたものとします。協力幅(ba)の算定については、“断面性能の計算式"を参照してください
a) 梁の許容曲げモーメント( $M_A$)
長方形梁の許容曲げモーメント( $M_A$)は、RC規準13条により次式で算定します。また、T形梁で上端引張になる場合においても、スラブを無視した長方形梁として次式で算定します。
$$M_A = C \cdot b \cdot d^2$$$M_A$:許容曲げモーメント
Cは以下に求める $C_1,C_2$のうち小さいほうの数値とします。
$C_1 = \frac{p_t \cdot f_c}{3 \cdot x_n} (n \cdot (1-x_{n1})(3-x_{n1})-\gamma \cdot (n-1)(x_{n1}-d_{c1})(3 \cdot d_{c1}-x_{n1}) )$ $C_2 = \frac{p_t \cdot f_c}{3 \cdot n \cdot (1-x_{n1}} (n \cdot (1-x_{n1})(3-x_{n1})-\gamma \cdot (n-1)(x_{n1}-d_{c1})(3 \cdot d_{c1}-x_{n1}) )$$d_c$:圧縮縁から圧縮鉄筋重心までの距離(=dt)(mm)
$d_{c1}$=dc/d
$f_c$:コンクリートの設計基準強度(N/mm2)
$n$:ヤング係数比
$γ$:複筋比(=ac/at)
$p_t$:引張鉄筋比(=at/(b・d))
$x_n$:圧縮縁より中立軸までの距離(mm)
$x_{n1} = p_t \cdot \left[ \sqrt({ n \cdot (1+\gamma)-\gamma )^2+ \frac{2}{p_t} ( n \cdot (1+\gamma \cdot d_{c1})-\gamma \cdot d_{c1} ) } - ( n \cdot (1+\gamma)-\gamma ) \right]$$p_{tb}$:釣合鉄筋比
$P_{tb} = \frac{1}{ 2 \cdot \left( 1+ \frac{f_t}{n \cdot f_c} \right) \cdot \left[ \frac{f_t}{n \cdot f_c} ( n+(n-1) \cdot \gamma \cdot d_{c1}-(n-1) \cdot \gamma \cdot(1-d_{c1}) \right]}$引張鉄筋比( $p_t$)が釣合鉄筋比( $p_{tb}$)以下の場合は、許容曲げモーメント( $M_A$)を次式により算定します。T形梁で下端引張になる場合においても、一般に有効幅(B)が大きいためにほとんどが釣合鉄筋比以下となることから、次式により算定します。また、釣合鉄筋比が負の場合においても次式により算定します。
$$M_A = \alpha_t \cdot f_t \cdot j$$$f_t$:引張鉄筋の許容引張応力度(N/mm2)
b) 梁主筋の2段筋重心位置
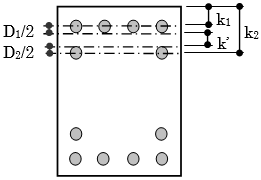
梁主筋の2段筋重心位置は、ユーザーによる入力がない場合、鉄筋コンクリート造配筋指針・同解説(以下、RC配筋指針と記します)により次式で算定します。
$$k_2 = k_1+ \frac{D_1}{2}+k'+ \frac{D_2}{2}$$$k_1$:1段筋重心位置(mm)
$k_2$:2段筋重心位置(mm)
$D_1$:1段筋最外径(mm)
$D_2$:2段筋最外径(mm)
$k'$:鉄筋のあき(mm)
$k' = \max (25, \quad 1.5 \cdot d')$ $d' = (d_1+d_2)/2$$d_1$:1段筋径(呼び名の数値)
$d_2$:2段筋径(呼び名の数値)
■ 重心位置の入力について
1段筋重心位置( $k_1$)は、①と②の2通りの入力方法があります。両方を入力した場合は、②による入力値が優先されます。
2段筋重心位置( $k_2$)は②による個別入力のみに対応しています。未入力の場合は内部計算値を採用します。
①メインメニュー「使用材料」→「鉄筋」→「鉄筋重心位置」で、方向および階ごとに一括で入力できます。デフォルト値は75mmです。
②メインメニュー「RC大梁リスト」→「詳細」で、符号ごとに個別に入力できます。
c) 異種強度梁の場合
異種強度梁の曲げに対する許容応力度検定は、圧縮側のコンクリート強度(上端引張の場合
$F_{cd}$, 下端引張の場合
$F_{cu}$)を用いて既存の方法で行います。
なお、T形梁による耐力計算を選択した場合、長方形梁とT形梁で耐力が大きくなる方を採用します。
せん断力に対する検討
梁の長期および短期の許容せん断力が設計用せん断力以上であることを、以下の検定式により確認します。
$ Q_L/Q_{AL} \verb|≦| 1.0 $ 長期せん断力に対する検定
$ Q_D/Q_{AS} \verb|≦| 1.0 $ 短期せん断力に対する検定
a) 梁の許容せん断力( $Q_A$)
■ 長期許容せん断力( $Q_{AL}$)
梁の長期許容せん断力( $Q_{AL}$)は、長期荷重によるせん断ひび割れの発生を前提とした下式により算定します。
$$Q_{AL} = b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_s(p_w-0.002) )$$ $α = \frac{4}{\frac{M}{Q \cdot d}+1}$かつ
$1.0 \verb|≦| \alpha \verb|≦| 2.0$とする。
$Q_{AL}$:長期許容せん断力
$f_s$:コンクリートの長期許容せん断応力度(N/mm2)
$_{w}f _{t}$:せん断補強筋の長期許容引張応力度(N/mm2)
$p_w$:せん断補強筋比(= $a_w/(b・x)$)
$p_w$の値が0.6%を超える場合は0.6%とする。
$a_w$:1組のせん断補強筋の断面積(mm2)
x:せん断補強筋の間隔(mm)
■ 短期許容せん断力( $Q_{AS}$)
梁の短期許容せん断力( $Q_{AS}$)は下式により算定します。
$$ Q_{AS} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle b \cdot j (\frac{2}{3} \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_s(p_w-0.002) ) & \displaystyle \left( \text{損傷制御のための検討} \right) \\ \displaystyle b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_s(p_w-0.002) ) & \displaystyle \left( \text{安全確保のための検討} \right) \end{array} \right. \end{align} $$ $\alpha = \frac{4}{\frac{M}{Q \cdot d}+1}$かつ
$1.0 \verb|≦| \alpha \verb|≦| 2.0$とする。
$Q_{AS}$:短期許容せん断力
$f_s$:コンクリートの短期許容せん断応力度(N/mm2)
$_wf _s $:せん断補強筋の短期許容引張応力度(N/mm2)
$p_w$:せん断補強筋比(= $a_w/(b・x)$)
1.2%を超える場合は1.2%とする。
・ $α$の算定に用いるせん断スパン比( $M/Q_d$)は、各検定位置のうちモーメントが最大となる位置の値を採用します。このとき、せん断力( $Q$)に水平荷重時割増係数( $n$)は考慮しません。
b) 梁の設計用せん断力( $Q_D$)
梁の短期設計用せん断力( $Q_D$)は、ユーザー選択注2)により $Q_{D1}$と$Q_{D2}$のいずれか、または小さいほうとします。
$$Q_D = \min (Q_{D1}, Q_{D2})$$ $$ Q_{D1} = \begin{align} \left\lbrace \begin{array}{ll} \displaystyle Q_0+ \frac{\sum {_B}M_y}{l} & \displaystyle \left( \text{MK785の場合} \right) \\ \displaystyle Q_L+ \frac{\sum {_B}M_y}{l} & \displaystyle \left( \text{上記以外の鉄筋の場合} \right) \end{array} \right. \end{align} $$ $$Q_{D2} = Q_L+ n \cdot Q_E$$$Q_D$:短期設計用せん断力
$Q_L$:長期設計用せん断力
$Q_0$:単純梁の長期せん断力
$Q_E$:地震荷重によるせん断力
$n$:水平荷重時せん断力の割増係数
$Σ_BM _y $:梁両端の降伏曲げモーメントの絶対値の和(= $ΣM_u $)
梁の曲げ終局強度( $M_u$)は5.1.1(2)を参照してください。このとき、 $M_u$にスラブ筋は考慮しません。
※積雪時、暴風時の短期設計用せん断力は以下とします。
・積雪時: $Q_D=Q_L+Q_{sn}$
・暴風時: $Q_D=Q_L+Q_w$
c) 高強度せん断補強筋を使用する場合について
■せん断補強筋比( $p_w$)
高強度せん断補強筋を使用する場合は、許容せん断力( $Q_A$)算定時に用いるせん断補強筋比( $p_w$)の制限値を以下とします。
| 製品名 | 長期pw | 短期pw |
|---|---|---|
| ウルボン1275【SBPD1275】BCJ評定-RC0220-05 MSRB-9009 | 0.6% | 1.2%(損傷制御) 1.0%(安全性確保) |
| リバーボン1275【SBPDN1275/1420】 | 0.6% | 0.8% |
| ウルボン785【UB785】 | 0.6% | 1.2%(損傷制御) 1.0%(安全性確保) |
| リバーボン785【KW785】 | 0.6% | 0.8% |
| スミフープ,ストロングフープ,デーフープ【KSS785】 | 0.6% | 0.8% |
| UHYフープ【SHD685】 | 0.6% | 1.2% |
| エヌエスハイデック685H【HDC685】 | 0.6% | 0.8% |
| スーパーフープ【KH785】 GBRC評定 第10-10号改 平成23年9月27日 MSRB-0061 | 0.6% | 1.2% もしくは 1.0%×(Fc/27)の小さい方 |
| スーパーフープ【KH685】 SABTEC評価 15-02 MSRB-0087 | 0.6% | 1.2% もしくは 1.2%×(Fc/27)の小さい方 |
| パワーリング785【SPR785】 BCJ評定-RC0395-02 MSRB-0066 | 0.6% | 1.2%(損傷制御) 1.0%(安全性確保) |
| パワーリング685【SPR685】 SABTEC評価15-03 MSRB-0094 | 0.6% | 1.2% もしくは 1.2%×(Fc/27)の小さい方 |
| エムケーフープ785【MK785】 BCJ評定-RC0419-03 MSRB-0067 | 0.6% | 1.2% |
■許容せん断力( $Q_A$)
高強度せん断補強筋を使用する場合の許容せん断力( $Q_A$)は下式で算定します。
【ウルボン1275の場合】
$$Q_{AS} = \phi \cdot b \cdot D \cdot \left( 850 \cdot \sqrt{\frac{W_0}{D} \cdot \frac{p_W}{_L\sigma_0+3} }\cdot \frac{M}{Q \cdot D}+1 \right) \cdot _L\tau_{SC}$$ $W_0 = \frac{W_a}{3 \cdot Q_L/(Q_L+Q_E)+1}$$_L\tau_{SC}$ = $\sqrt{\sigma_T{^2}+\sigma_T \cdot {_L\sigma}_0}/\kappa$
(損傷制御のための検討)
・ $M/(Q・D)$が2.0を超える場合は2.0とします。
・ $_Lσ_0$が0以下の場合、 $_Lτ _{SC} $の算定では負として扱い、 $ Q _{AS} $算定では0として扱います。
・ $_Lσ_0$が18N/mm2を超える場合、 $_Lσ_0$が18N/mm2とします。
また、損傷制御のための検討を選択していた場合でも、基礎梁および軽量コンクリートは対象外のため、安全性確保として検討します。
(安全性確保のための検討)
$Q_{AS} = b \cdot j( \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001))$$f_s$は軽量コンクリートの場合、0.75倍とします。
【スーパーフープKH785,KH685の場合】
$Q_{AL} = b \cdot j ( \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.002))$$Q_{AS} = b \cdot j (\beta_c \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.002))$ (損傷制御のための検討)
$Q_{AS} = b \cdot j ( \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.002))$ (安全確保のための検討)
$β_c:1-(100pw-0.2)/3$$Q_{AL}$:長期許容せん断力
$Q_{AS}$:短期許容せん断力
【パワーリング785の場合】
SPR785の損傷制御のための検討、安全性確保のための検討は下式で算定します。
$Q_{AS} = b \cdot j (2/3 \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (損傷制御のための検討)
$Q_{AS} = b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (安全確保のための検討)
また、損傷制御のための検討を選択していた場合でも、梁せいが1000mmを超える梁部材、基礎梁については安全性確保のための検討で算定します。
【パワーリング685の場合】
SPR685の損傷制御のための検討、安全性確保のための検討は下式で算定します。
$Q_{AS} = b \cdot j (\beta_c \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001))$ (損傷制御のための検討)
$ Q_{AS} = b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) ) $ (安全確保のための検討)
$β_c$は以下の式を用いるか、2/3とするか選択できます。ただし、梁内法スパン長比が3.0未満の場合、$β_c$=2/3とします。
$\beta_c = 1-(100p_w-0.2)/3$【エムケーフープの場合】
MK785の損傷制御のための検討、安全性確保のための検討は下式で算定します。
$Q_{AS} = b \cdot j (2/3 \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (損傷制御のための検討)
$Q_{AS} = b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (安全確保のための検討)
また、損傷制御のための検討を選択していた場合でも、梁せいが1000mmを超える梁部材については安全性確保のための検討で算定します。
【上記以外の高強度せん断補強筋の場合】
$Q_{AS} = b \cdot j (2/3 \cdot \alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (損傷制御のための検討)
$Q_{AS} = b \cdot j (\alpha \cdot f_s+0.5 \cdot {_w}f_t(p_w-0.001) )$ (安全確保のための検討)
※上式は暫定対応による計算となっています。メーカーの設計指針と計算内容が異なる場合があります。
注2) メインメニュー「設計・計算条件」→「断面算定条件」→「RC造」参照。
d) 異種強度梁の場合
異種強度梁のせん断に対する許容応力度検定は、等価平均強度
$F_{ce}$による許容せん断応力度を用います。
等価平均強度は以下のように計算されます。
ただし、等価平均強度は梁下部のコンクリート強度を上限とします。
$A_u$ : 梁上部の断面積(スラブの協力幅含む) $A_d$ : 梁下部の断面積 $F_{cu}$ : 梁上部のFc $F_{cd}$ : 梁下部のFc