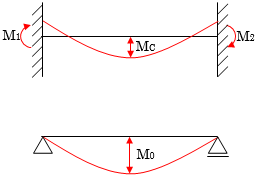
採用応力

■モーメント分布

曲げモーメントの分布は２次曲線と仮定して以下の式で計算します。

$M_{1},M_{2}$ ：端部モーメント

$M_{0}$ ：単純梁の中央モーメント

$x$ ：応力採用位置

$L$ ：材長

■一本部材指定時の採用応力

大梁において一本部材指定を行った場合のM0は、端部のせん断力と釣り合う荷重が等分布として単純梁に作用したものと仮定した場合のA式もしくは,一本部材とした場合の中央位置におけるモーメントを中央に位置する分割部材の端部モーメントおよびM0から算出した場合のB式のうち、大きい数値を採用します。

A. 　　 $ M_0 = \frac{(Q_1+Q_2) \cdot L}{8} $

$Q_1,Q_2$ ：端部せん断力

$L$ ：材長

B. 　　 $ M_c = M_{c1}+\frac{(-M_{c1}-M_{c2}+4M_{c0}) \cdot x}{L} -\frac{4M_{c0} \cdot x^2}{L^2}$

$M_1,M_2$ ：一本部材の端部モーメント

$M_0$ ：一本部材の単純梁中央モーメント

$M_{c1},M_{c2}$ ：中央部分割部材の端部モーメント

$M_{c0}$ ：中央部分割部材の単純梁中央モーメント

$x$ ：中央部分割部材の応力採用位置

$L$ ：中央部分割部材の材長

$M_c$ ：一本部材の中央モーメント

■大梁直交方向加力時採用応力

　大梁の採用応力は、各水平荷重加力ケースにおいて最大せん断力が発生するケースを採用応力とします。したがって、加力方向を0°方向・90°方向としていない場合もしくは大梁がX軸、Y軸に平行でない場合には、大梁の方向と異なる加力ケースの応力が採用される場合があります。その場合、計算書出力の断面検定表においてその旨が出力されます。