段階的耐力喪失解析
段階的耐力喪失解析
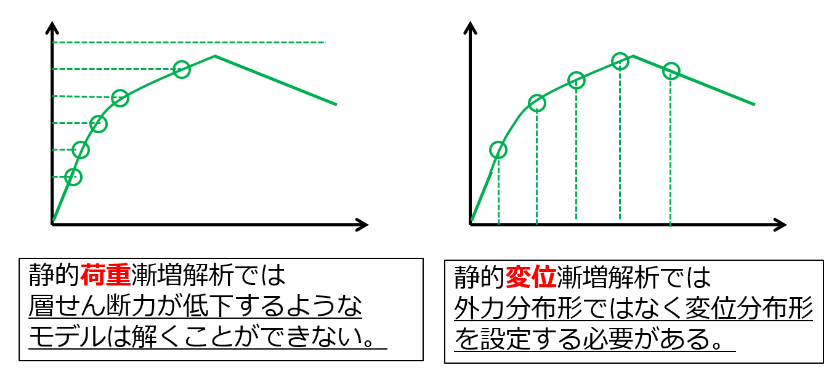
荷重漸増解析において、擬似的に耐力劣化を考慮する解析です。 通常の荷重漸増解析では、荷重が減少するような層として耐力劣化を生じる計算を行うことはできません。
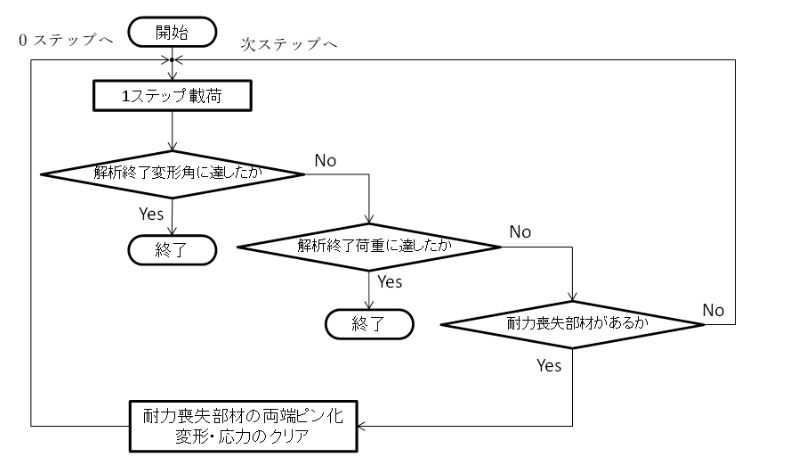
段階的耐力喪失解析では、以下のように擬似的に耐力劣化を考慮します。
- 耐力喪失変形角を設定します。
- せん断降伏後耐力喪失変形角に達する部材が発生するまで荷重漸増を行います。
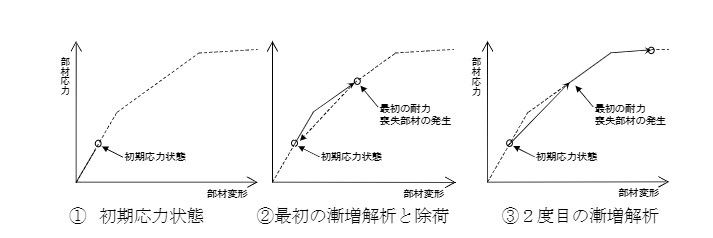
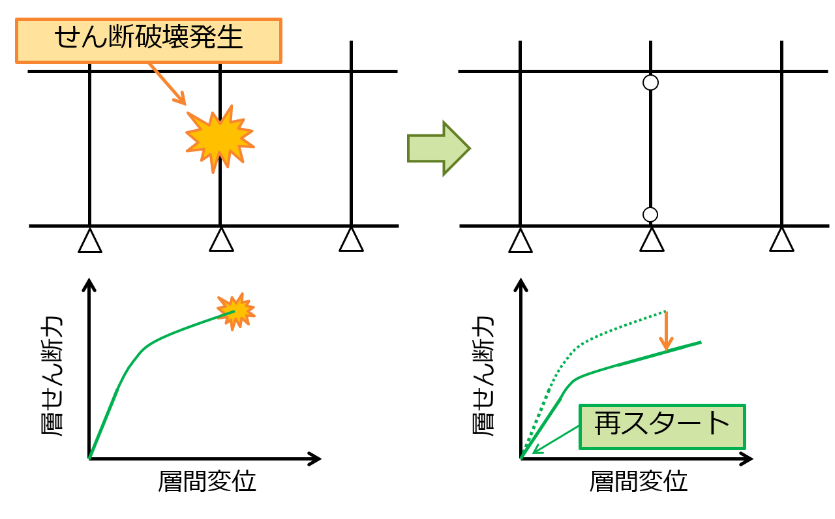
- 耐力喪失変形角に達した部材が発生した場合、当該部材を両端ピンとしてせん断力を負担しない部材に変更したのち荷重を0から再載荷します。
- これを繰り返し、得られた荷重変形関係を包絡することで耐力劣化を考慮した曲線を得ます。
耐力喪失変形角直接指定の場合
耐力喪失開始変形角と終了変形角を指定します。
せん断降伏後、終了変形角を超えた部材が発生した際に、開始変形角を超える部材はまとめて両端ピンとして再載荷を行います。
FEMAによる非線形特性設定の場合
大梁
FEMAを用いた段階的耐力喪失解析を行う場合、以下のように計算されます。
各範囲内における塑性回転角は線形補間により算出します。
$b$: 梁幅
$D$: 梁せい
$\rho$ : 引張側鉄筋比
$\rho'$ : 圧縮側鉄筋比
$\rho_{bal}'$ : 釣り合い鉄筋比
$s$: せん断補強筋間隔
$V_s$: せん断耐力
$V$: 両端降伏時せん断力
$f_c'$: コンクリート強度(N/mm2)
“C”, “NC” は以下のように判定します。 “C” : $s <= D / 3 $ かつ $ Vs >= 0.75 * V $
塑性回転角は以下のように算出されます。 塑性回転角に達した梁は耐力喪失部材として除去されます。
| $\frac{\rho-\rho'}{\rho_{bal}} $ | $C/NC$ | $\frac{V}{bd\sqrt{f_c'}}$ | 塑性変形角 $a(rad)$ |
|---|---|---|---|
| ≦0.0 | C | ≦0.25 | 0.025 |
| ≦0.0 | C | ≧0.5 | 0.02 |
| ≧0.5 | C | ≦0.25 | 0.02 |
| ≧0.5 | C | ≧0.5 | 0.015 |
| ≦0.0 | NC | ≦0.25 | 0.02 |
| ≦0.0 | NC | ≧0.5 | 0.01 |
| ≧0.5 | NC | ≦0.25 | 0.01 |
| ≧0.5 | NC | ≧0.5 | 0.005 |
柱
柱については現状未対応となります。