ブレースの剛性
一般ブレースの剛性
一般ブレースの剛性計算は、下式によって求めます。 引張専用ブレースとした場合、引張となるブレースと圧縮となるブレースが対になって存在すると考え、弾性解析では剛性を1/2としてモデル化します。弾塑性解析の場合は初期剛性は1倍としてモデル化されます。
$K_B = \frac{EA}{L}$
ここで、
$L$:芯々間の長さ
$A$:降伏部の断面積
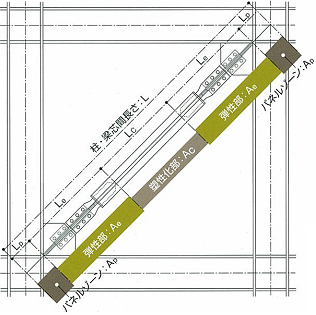
日鉄エンジニアリングアンボンドブレースの剛性
アンボンドブレースの1次剛性は下式により計算します。
$K_1 = \phi_A\times \frac{EA_c}{L}$
$φ_A$:等価剛性倍率
$L$:芯芯間の長さ
$A_c$:塑性化部断面積
等価剛性倍率の計算例を以下に示します。
$\phi_A = \frac{1}{\alpha+2\beta \frac{A_c}{A_e}+(1-\alpha-2\beta ) \frac{A_c}{A_p}}$
ここで、
$α$ :塑性化部長さの柱・梁芯間長さに対する比(= $L_c/L$)
$β$ :弾性部長さの柱・梁芯間長さに対する比(= $L_e/L$)
$A_c/A_e$ : 塑性化部断面積の弾性部断面積に対する比
$A_c/A$p$ : 塑性化部断面積のパネルゾーン断面積に対する比
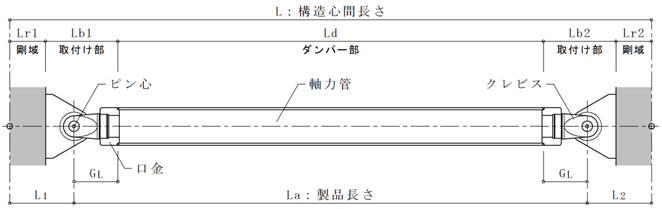
JFEシビル KTブレースの剛性
JFEシビルKTブレースの剛性計算は下式によって求めます。
$K_B = \frac{EA}{L}$ ここで、
$L$:構造心間長さ
$A$:軸力管の断面積
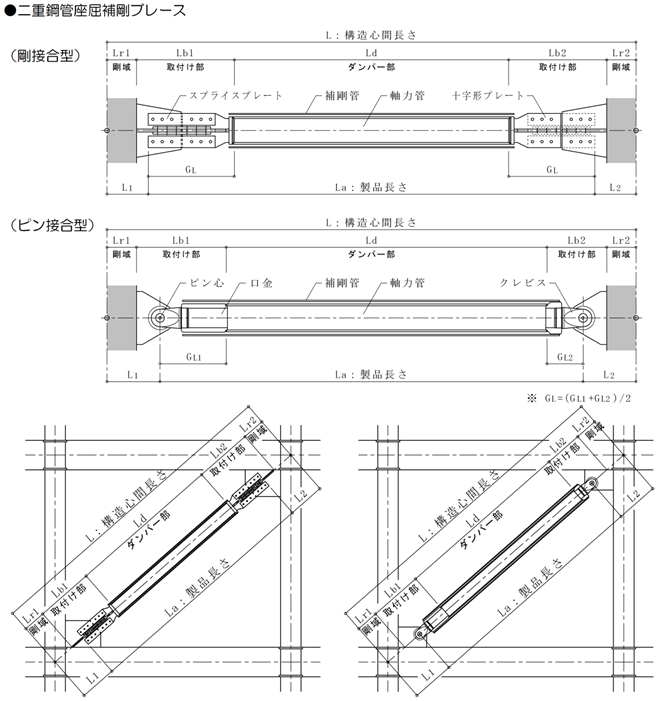
JFEシビル 二重鋼管座屈補剛ブレースの剛性
JFEシビル二重鋼管座屈補剛ブレースの剛性計算は以下によって求めます。
剛性計算を「自動」とした場合、JFEシビル二重鋼管座屈補剛ブレースの剛性計算は下式によって求めます。
$\frac{1}{K_e} = \frac{1}{K_d}+\frac{1}{K_b}+\frac{1}{K_r}, \quad K_d = \frac{E \cdot A_d}{L_d}, \quad K_b = \frac{b \cdot E \cdot A_d}{L_b}, \quad K_r = \frac{E \cdot A_r}{L_r} = \infty$$K_e$ : ブレース剛性
$K_d$ : ダンパー部剛性
$K_b$ : 取付け部剛性
$K_r$ : 剛域部剛性
$b : 取付け部断面積比(=$A_b/A_d$)
$L_d$ : ダンパー部長さ
$L_b$ : 取付け部長さ
$L_r$ : 剛域部長さ
$A_d$ : ダンパー部
$A_b$ : 取付け部断面積
$A_r$ : 剛域部断面積(=∞)
ダンパー部長さ、取付け部長さを以下のように計算します。
$L_d = d \cdot L, \quad L_b = (1-d-r) \cdot L, \quad L_r = L-L_d-L_r$$d$ : ダンパー部長さ
$r$ : 剛域部長さ
$L$ :構造芯間長さ
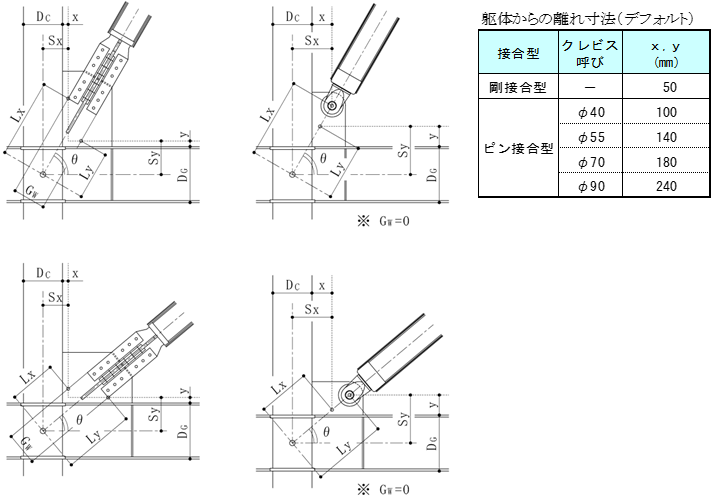
ダンパー部長さ比、剛域長さ比は以下のように計算します。
$d = 1-\frac{\max (L_{x1},L_{y1})+\max (L_{x2},L_{y2}) +2 \cdot G_L}{L}$ $L_{x1} = S_{x1}/ \cos \theta+0.5 \cdot G_w \cdot \tan \theta$ $L_{y1} = S_{y1}/ \sin \theta+0.5 \cdot G_w/ \tan \theta$ $S_{x1} = 0.5 \cdot D_{C1}+x1$ $S_{y1} = 0.5 \cdot D_{G1}+y1$ $L_{x2} = S_{x2}/ \cos \theta+0.5 \cdot G_w \cdot \tan \theta$ $L_{y2} = S_{y2}/ \sin \theta+0.5 \cdot G_w/ \tan \theta$ $S_{x2} = 0.5 \cdot D_{C1}+x2$ $S_{y2} = 0.5 \cdot D_{G1}+y2$ $r = \frac{\max (R_{x1},R_{y1})+\max (R_{x2},R_{y2})}{L}$ $R_{x1} = 0.5 \cdot D_{C1}/ \cos \theta$ $R_{y1} = 0.5 \cdot D_{G1}/ \sin \theta$ $R_{x2} = 0.5 \cdot D_{C2}/ \cos \theta$ $R_{y2} = 0.5 \cdot D_{G2}/ \sin \theta$剛性計算を「倍率指定」とした場合、JFEシビル二重鋼管座屈補剛ブレースの剛性計算は下式によって求めます。
$K_e = \alpha \cdot K_d, \quad K_d = \frac{E \cdot A_d}{L}$$L$ : 構造芯間長さ
$K_e$ : ブレース剛性
$K_d$ : ダンパー部合成
$α$ : 指定倍率