S大梁
S梁の剛性
断面積
梁の断面積は、角形鋼管のコーナー部分、H形鋼のフィレット部分などを考慮した実断面積とします。
合成梁の断面性能
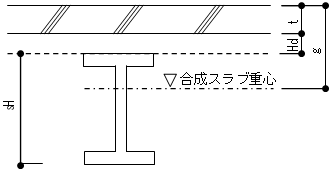
梁が合成梁の場合の断面性能を自動計算します。合成梁の剛性は、下式で求められるスラブを考慮した剛性と鉄骨梁のみの剛性の平均とします。
$g = \frac{_cE \cdot B \cdot t \cdot (t/2)+_sE \cdot _sA \cdot (t+Hd+_sH/2)}{_cE \cdot B \cdot t+_sE \cdot _sA}$ $I = \left( \frac{_cE}{_sE} \right) \cdot \left( \frac{B \cdot t^3}{12} +B \cdot t \cdot (g-t/2)^2 \right) +_sI+_sA \cdot (g-t-Hd-_sH/2)^2$ここで、
$_cE$ :コンクリートのヤング係数
$_sE$ :鋼材のヤング係数
$_sA$ :鋼材の断面積
$_sI$ :鋼材の断面2次モーメント
$t$ :スラブの厚さ(計算条件の剛性で入力した値)
$Hd$ :デッキ高さ(計算条件の剛性で入力した値)
断面欠損の考慮
(フランジ)
継手部の断面欠損を考慮する場合、ユーザー指定の低減値によりフランジ幅を低減します。
(ウェブ)
継手部およびスカラップによる断面欠損を考慮する場合には、ユーザー指定の低減値によりウェブ板厚を一律に低減します。
S大梁の断面性能
軸断面積( $A_n$)
柱・梁の軸断面積( $A_n$)は、次式により算定します。
$A_n=A$$A$:鉄骨全断面積( $mm^2$)
せん断変形用断面積( $A_S$)
$A_s=\frac{A_w}{\kappa}$$κ$:形状係数(=1.0)
断面2次モーメント( $I$)
H形 : $I = \frac{BH^3-(B-t_w)(H-2t_f)^3}{12}$
角型鋼管 : $I = \frac{BH^3-(B-2t_w)(H-2t_f)^3}{12}$
円形鋼管 : $I = \frac{\pi (D^4-d^4)}{64}$
$H$ :鉄骨梁せい (mm)
$B$ :フランジ幅 (mm)
$t_f$ :フランジ厚 (mm)
$t_w$ :ウェブ厚 (mm)
ねじり断面2次モーメント( $J$)
指定により、ねじり剛性を考慮することが可能です。
H形 : $J = \frac{1}{3} \left( 2 \cdot B \cdot t_f^3+(H-2 \cdot t_f) \cdot t_w^3 \right)$