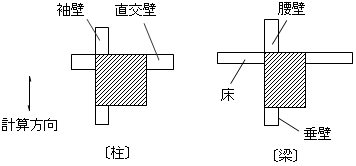
RC柱

RC柱の剛性

剛性増大率

軸断面積

柱の軸断面積は袖壁および直交袖壁を考慮し、せん断断面積には直交袖壁は無視し袖壁のみ考慮します。袖壁のヤング係数は母材と同じと仮定します。

断面2次モーメント

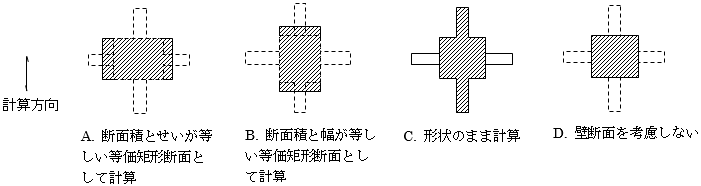
柱の断面2次モーメントの算定方法は、下記のいずれかの選択により設定できます注1）。 $A～C$を選択した場合は、直交壁は無視し、袖壁のみを評価して断面2次モーメントを求めます。求めた断面2次モーメントと元の断面の断面2次モーメントの比率を剛性増大率として設定します。

※「鉄筋・鉄骨の剛性を考慮する」とした場合には剛性増大率は変化せず、剛性増大率を乗じる元となる断面2次モーメントを増大させます。

RC柱の断面性能

鉄筋コンクリート造柱の断面性能の計算は以下によります。

軸断面積（ $A_n$）

柱の軸断面積（A_n）は、鉄筋を考慮して次式により算定します。

$A_n = ({B \cdot (D-t)+B \cdot t+(n-1) \sum \alpha_i}) \cdot \frac{l_0}{l}$

$n$：ヤング係数比

$l_0$：可撓長さ（剛域を考慮した長さ）（mm）

$l$：節点間長（mm）

せん断変形用断面積（ $A_S$）

$A_s = \frac{B \cdot D}{\kappa}$

$κ$：形状係数（＝1.2）

断面2次モーメント（ $I_e$）

鉄筋コンクリート造柱の断面2次モーメント（ $I_e$）は鉄筋を考慮して次式により算定します。

$I_e = \frac{B \cdot D^3}{12}+ \frac{(b-B)t^3}{12}+B \cdot D \cdot (g-D/2)^2+(b-B) \cdot t \cdot (D-t/2-g)^2+(n_r-1) \sum \alpha_i(g-y_i)^2$ $g = \frac{1/2b \cdot D^2+(b-B) \cdot t \cdot (D-t/2)+(n_r-1) \sum \alpha_i \cdot y_i}{B \cdot D+(b-B) \cdot t+(n_r-1) \sum \alpha_i}$

$g$：梁下端から図心位置までの距離（mm）

ねじり断面2次モーメント（ $J$）

指定により、ねじり剛性を考慮することが可能です。壁、床が取付かない元断面に対してねじり剛性を次式で算定します。

矩形 :

$J = \frac{B^3 \cdot D}{16} \cdot \left[ \frac{16}{3}-3.36 \cdot \frac{B}{D} \cdot \left( 1-\frac{1}{12} \cdot \left( \frac{B}{D} \right)^4 \right) \right]$

円形 :
$J = \frac{\pi r^4}{2}$