RC大梁
RC大梁の剛性
剛性増大率
軸断面積
梁の断面積は腰壁・垂壁を考慮します。腰壁・垂壁のヤング係数は母材と同じと仮定します。
断面二次モーメント
梁の断面2次モーメントは、柱と同じ算定方法により計算します 注1)。
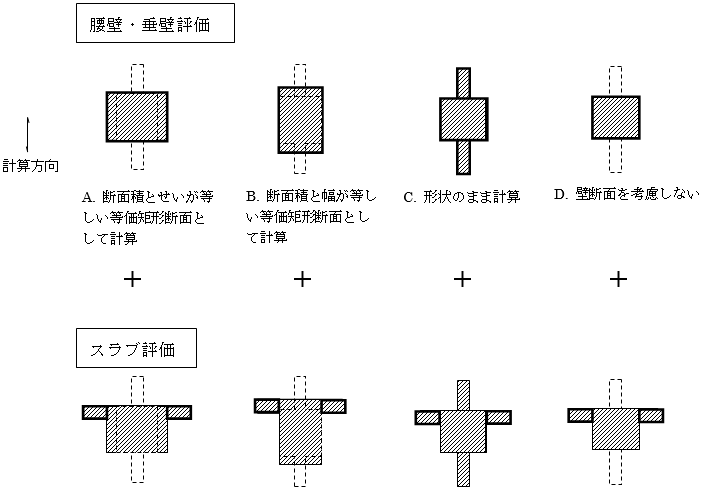
$A~C$を選択した場合は、腰壁・垂壁を評価して断面2次モーメント
$I$を求めます。上記の
$A$または
$B$の評価は腰壁・垂壁のみについて等価断面として考慮し、床は別途計算し加算します。
$C$の評価の場合、腰壁・垂壁および床をすべて形状通り評価します。中立軸はいずれの場合も床スラブを考慮した中立軸を採用します。床の厚さは、建物全体で一律に設定できます 注1)。
床については、
$A$.協力幅による自動計算、または
$B$.剛性増大率の直接入力により剛性の評価方法を設定できます 注1)。二重スラブとして配置した床は、荷重のみを評価して剛性は考慮しません。また、片持ちスラブを剛性として考慮するかどうかについては「剛性条件」により設定できます。
※「鉄筋・鉄骨の剛性を考慮する」とした場合には剛性増大率は変化せず、剛性増大率を乗じる元となる断面2次モーメントを増大させます。
注1) メインメニュー「設計・計算条件」→「剛性条件」参照。
協力幅の計算
a) 協力幅による自動計算
協力幅はRC規準8条「構造解析の基本事項」により算定します。床の厚さは建物全体で一律に設定します注1)。
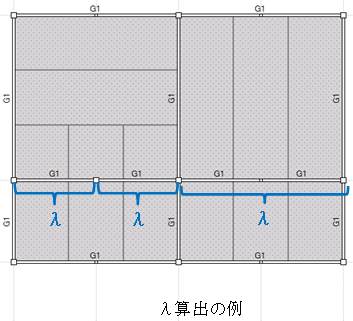
床組みを構成する大梁のうち以下のすべての条件を満たす大梁群は連続梁と見なしてλを算出します。
・方向が同じ大梁
・直線上に配置されている大梁
・中間に柱が存在しない
- λ算出の例
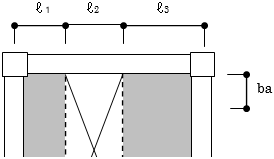
吹抜けがある場合は、床の長さの比を倍率としてbaにかけて算定します。
$ba' = \frac{l_1+l_3}{l_1+l_2+l_3} \cdot ba$※床荷重リストで床厚を0[mm]とした床は吹抜けと同様に扱います
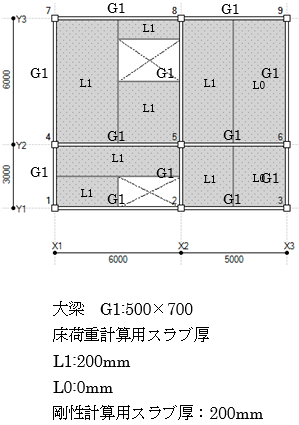
協力幅の計算例を以下に示します。
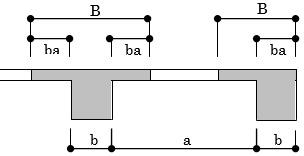
下図のような平面において、
(大梁1-2の場合)
$ba = \left( 0.5-0.6\times\frac{2.5}{6.0} \right) \times2.05\times \frac{3.0}{3.0+3.0}=0.313$
$B = 0.5+0.313 = 0.813$
(大梁2-3の場合)
$ba = 0.1\times5.0\times \frac{2.5}{2.5+2.5}=0.250$
$B = 0.5+0.250 = 0.750$
(大梁5-8の場合) $ba1 = 0.1\times6.0\times \frac{3.0+1.0}{3.0+2.0+1.0}=0.4000$
$ba2 = 0.1\times6.0=0.6000$
$B = 0.5+0.400+0.6000=1.500$
(大梁8-9の場合)
$ba = 0.1\times5.0\times \frac{2.5}{2.5+2.5}=0.250$
$B = 0.5+0.250=0.750$
b) 剛性増大率の直接入力
片側スラブ、両側スラブごとに剛性増大率を用いて算定します。
構造スラブ符号指定
床に対して構造スラブ符号を指定した場合、梁上部のコンクリートは梁に指定したコンクリート材料によるヤング係数を採用し、梁の片側もしくは両側に取り付くスラブについては設定した構造スラブのコンクリート材料によるFcを採用します。
RC大梁の断面性能
鉄筋コンクリート造梁の断面性能の計算は以下によります。
軸断面積( $A_n$)
梁の軸断面積( $A_n$)は、鉄筋を考慮して次式により算定します。
$A_n=({B \cdot (D-t)+B \cdot t+(n-1) \sum \alpha_i}) \cdot \frac{l_0}{l}$$n$:ヤング係数比
$l_0$:可撓長さ(剛域を考慮した長さ)(mm)
$l$:節点間長(mm)
異種強度梁の場合、補正したヤング係数 $E_{ce}$に、軸断面積 $A_n$を乗じて算定します。 補正ヤング係数は以下のように算出します。
$E_{ce}=E_{cu} \cdot T/D + E_{cd} \cdot (D-T)/D$ここで、
・
$E_{cu}=3.35 \cdot 10^4 \cdot (\gamma_u/24)^2 \cdot (F_{cu}/60)^{1/3}$ (単位:N/mm2)
・
$E_{cd}=3.35 \cdot 10^4 \cdot (\gamma_d/24)^2 \cdot (F_{cd}/60)^{1/3}$ (単位:N/mm2)
・
$\gamma_u$,
$\gamma_d$:それぞれ梁上部, 梁下部コンクリートの単位体積重量
・
$F_{cu}$,
$F_{cd}$:それぞれ梁上部, 梁下部コンクリート強度
せん断変形用断面積( $A_S$)
$A_s=\frac{B \cdot D}{\kappa}$$κ$:形状係数(=1.2)
異種強度梁の場合、補正したせん断弾性係数 $G_{ce}$に、せん断断面積 $A_s$(RESP-D計算編マニュアルに従います)を乗じて算定します。
異種強度梁のせん断弾性係数 $G_{ce}$は、補正したヤング係数 $E_{ce}$より下式により算定します。
$G_{ce}=E_{ce}/\{2(1+\nu)\}$断面2次モーメント( $I_e$)
鉄筋コンクリート造梁の断面2次モーメント( $I_e$)は鉄筋を考慮して次式により算定します。
$I_e = \frac{B \cdot D^3}{12}+ \frac{(b-B)t^3}{12}+B \cdot D \cdot (g-D/2)^2+(b-B) \cdot t \cdot (D-t/2-g)^2+(n_r-1) \sum \alpha_i(g-y_i)^2$ $g = \frac{1/2b \cdot D^2+(b-B) \cdot t \cdot (D-t/2)+(n_r-1) \sum \alpha_i \cdot y_i}{B \cdot D+(b-B) \cdot t+(n_r-1) \sum \alpha_i}$$g$:梁下端から図心位置までの距離(mm)
大梁で構造スラブにより異なるFcを指定した場合、以下の計算となります。
$I_e = \frac{B \cdot D^3}{12}+ \frac{(b-B)t^3}{12} \cdot \frac{E_s}{E_g} +B \cdot D \cdot (g-D/2)^2+(b-B) \cdot t \cdot (D-t/2-g)^2 \cdot \frac{E_s}{E_g} +(n_r-1) \sum \alpha_i(g-y_i)^2$$E_g$ : 大梁コンクリートヤング係数
$E_s$: スラブコンクリートヤング係数
異種強度梁の場合、補正したヤング係数 $E_{ce}$を用いて算定します。
ねじり断面2次モーメント( $J$)
指定により、ねじり剛性を考慮することが可能です。壁、床が取付かない元断面に対してねじり剛性を次式で算定します。
矩形 :
$J = \frac{B^3 \cdot D}{16} \cdot \left[ \frac{16}{3}-3.36 \cdot \frac{B}{D} \cdot \left( 1-\frac{1}{12} \cdot \left( \frac{B}{D} \right)^4 \right) \right]$円形 :
$J = \frac{\pi r^4}{2}$